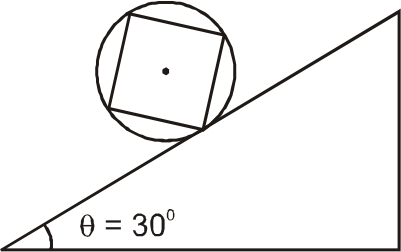
Four identical uniform rods of mass M=6kg each are welded at their ends to form a square and then welded to a uniform ring having mass m=4kg & radius R=1m the system is allowed to roll down on the rough and fixed incline of inclination θ=30∘ (assume no sliding anywhere)
Q. The minimum value of coefficient of friction to prevent slipping is-
57
512√3
5√37
75√3
The correct Answer is:B
i=⎡⎢
⎢
⎢⎣M(R√2)212+M(R√2)2⎤⎥
⎥
⎥⎦×4+mR2
=20kgm2.
(4M+m)gsinθ−F=(4M+m)a.
F.R.=I(aR)
Solving
a=7g24
F=20a≤μ(4M+m)gcos30
μ≥512√3
∴μmin=512√3

Similar Questions
For identical rods, each of mass m are welded at their ends to form a square, and the corners are then welded to a light metal hoop of radius r. If the rigid assembly of rods and hoop is allowed to roll down the inclined rough surface. If the minimum value of the coefficient of static friction which will prevent slipping is k10 . Find the value of k.
View SolutionA solid sphere of mass m rolls without slipping on an inclined plain of inclination θ. What should be the minimum coefficient of static friction to support pure rolling?
View Solution
Knowledge Check
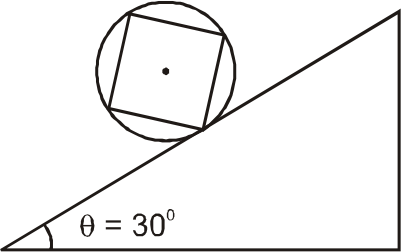
Four identical uniform rods of mass M=6kg each are welded at their ends to form a square and then welded to a uniform ring having mass m=4kg & radius R=1m the system is allowed to roll down on the rough and fixed incline of inclination θ=30∘ (assume no sliding anywhere)
Q. The acceleration of centre of mass of system isAg2Bg4C7g24Dg8
Four identical uniform rods of mass M=6kg each are welded at their ends to form a square and then welded to a uniform ring having mass m=4kg & radius R=1m the system is allowed to roll down on the rough and fixed incline of inclination θ=30∘ (assume no sliding anywhere)
Q. The moment of inertia of system about the axis of ring will be-A20kgm2B40kgm2C10kgm2D60kgm2A sphere of mass M rolls without slipping on the inclined plane of inclination θ. What should be the minimum coefficient of friction, so that the sphere rolls down without slipping ?
A2/5tanθB2/7tanθC5/7tanθDtanθ
A solid cylinder of mass 8 kg and radius 50 cm is rolling down a plane inclined at an angle of 30∘ with the horizontal. The minimum value of coefficient of friction so that cylinder does not slip while rolling down the plane.
View SolutionA hollow sphere of mass m and radius R is rolling downdard on a rough inclined plane of inclination θ. If the coefficient of friction between the hollow sphere and incline is μ, then
View SolutionA body of 5 kg weight kept on a rough inclined plane of angle 30∘ starts sliding with a constant velocity. Then the coefficient of friction is (assume g=10m/s2)
View SolutionA solid cylinder of mass m and radius r is rolling on a rough inclined plane of inclination θ. The coefficient of friction between the cylinder and incline is μ. Then.
View SolutionA uniform sphere of mass m and radius r rolls without slipping down a inclined plane, inclined at an angle 45∘ to the horizontal . Find the magnitude of frictional coefficient at which slipping is absent :
View Solution
