A body of 5 kg weight kept on a rough inclined plane of angle 30∘ starts sliding with a constant velocity. Then the coefficient of friction is (assume g=10m/s2)
1/√3
2/√3
√3
2√3
The correct Answer is:A
To solve the problem, we need to find the coefficient of friction (μ) for a body of weight 5 kg that is sliding down a rough inclined plane at a constant velocity. Given that the angle of inclination (θ) is 30 degrees and the acceleration due to gravity (g) is 10 m/s², we can follow these steps:
1. Identify the Forces Acting on the Body:
- The weight of the body (W) can be calculated as:
W=mg=5kg×10m/s2=50N
- The weight can be resolved into two components:
- Parallel to the incline: W∥=mgsinθ
- Perpendicular to the incline: W_{\perpendicular} = mg \cos \theta
2. Calculate the Components of Weight:
- For θ = 30 degrees:
W∥=50sin(30∘)=50×12=25N
W_{\perpendicular} = 50 \cos(30^\circ) = 50 \times \frac{\sqrt{3}}{2} = 25\sqrt{3} \, \text{N}
3. Determine the Normal Force (N):
- The normal force (N) acting on the body is equal to the perpendicular component of the weight:
N = W_{\perpendicular} = 25\sqrt{3} \, \text{N}
4. Apply the Condition for Constant Velocity:
- Since the body is sliding down with constant velocity, the net force acting along the incline is zero:
W∥−Fk=0
- Where Fk is the kinetic friction force, which can be expressed as:
Fk=μN
- Therefore, we have:
mgsinθ=μN
5. Substituting Known Values:
- Substitute W∥ and N:
25=μ(25√3)
6. Solving for the Coefficient of Friction (μ):
- Rearranging the equation gives:
μ=2525√3=1√3
- This can be simplified to:
μ=√33
Final Answer:
The coefficient of friction (μ) is:
μ=√33
- The weight of the body (W) can be calculated as:
W=mg=5kg×10m/s2=50N
- The weight can be resolved into two components:
- Parallel to the incline: W∥=mgsinθ
- Perpendicular to the incline: W_{\perpendicular} = mg \cos \theta
- For θ = 30 degrees:
W∥=50sin(30∘)=50×12=25N
W_{\perpendicular} = 50 \cos(30^\circ) = 50 \times \frac{\sqrt{3}}{2} = 25\sqrt{3} \, \text{N}
- The normal force (N) acting on the body is equal to the perpendicular component of the weight:
N = W_{\perpendicular} = 25\sqrt{3} \, \text{N}
- Since the body is sliding down with constant velocity, the net force acting along the incline is zero:
W∥−Fk=0
- Where Fk is the kinetic friction force, which can be expressed as:
Fk=μN
- Therefore, we have:
mgsinθ=μN
- Substitute W∥ and N:
25=μ(25√3)
- Rearranging the equation gives:
μ=2525√3=1√3
- This can be simplified to:
μ=√33
The coefficient of friction (μ) is:
μ=√33
Topper's Solved these Questions
Similar Questions
A block of wood of 1 kg resting on an inclined plane of angle 30∘, just starts moving down. If the coefficient of friction is 0.2, then find its velocity (in ms−1) after 5 s (take , g=10ms−2)
View SolutionA body weighing 20 kg just slides down a rough inclined plane that rises 5 m in every 13 m. What is the coefficient of friction?
View Solution
Knowledge Check
A block is projected upwards with a velocity of 5 m/s from the bottom of a rough inclined plane of inclination 30° with the horizontal. It stops after 0.5 s. What is the coefficient of friction ? (g=10m/s2)
A√3B1√3C√2D√5A body of mass M starts sliding down an Inclined plane where critical angle is <ACB=30∘ as shown in figure, the coefficient of friction will be
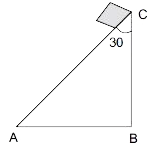 AMg√3B√3MgC√3DNone of these
AMg√3B√3MgC√3DNone of theseA block of mass 1 kg slides down on a rough inclined plane of inclination 60∘ starting from its top. If the coefficient of kinetic friction is 0.5 and length of the plane is 1 m , then work done against friction is (Take g=9.8m/s2)
A9.82 JB4.94 JC2.45 JD1.96 J
A body of mass 5×10−3 kg is launched upon a rough inclined plane making an angle of 30∘ with the horizontal. Obtain the coefficient of friction between the body and the plane if the time of ascent is half of the time of descent.
View SolutionA body of mass ‘m’ is launched up on a rough inclined plane making an angle of 30∘ with the horizontal. The coefficient of friction between the body and plane is √x5 if the time of ascent is half of the time of descent. The value of x is ___________.
View SolutionA block slides down on inclined plane (angle of inclination 60∘ ) with an accelration g/2 Find the coefficient friction

View SolutionA body of mass 5×10−3 kg is launched upon a rough inclined plane making an angle of 30∘ with the horizontal. Obtain the coefficient of friction between the body and the plane if the time of ascent is half of the time of descent.
View SolutionA block is at rest on an inclined plane making an angle α with the horizontal . As the angle α of the incline is increased the block starts slipping when the angle of inclination becomes θ. The coefficient of static friction between the block and the surface of the inclined plane is or A body starts sliding down at an angle θ to the horizontal. Then the coefficient of friction is equal to
View Solution

