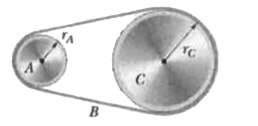
Wheel $A$ of radius $r_{A} = 10 c m$ is coupled by a belt $C$ to another wheel of radius $r_{B} = 25 c m$ as in the figure. The wheels are free to rotate and the belt does not slip . At time $t = 0$ wheel $A$ increases it's angular speed from rest at a uniform rate $π / 2 r a d / {sec}^{2}$ Find the time in which wheel $B$ attains a speed of $100 r \pm [$ Hint $: v_{A} = v_{B}]$

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $50 / 3 sec$ .

For no slipping condition
$r_{A} α_{A} = r_{B} α_{B}$
$\Rightarrow α_{B} = \frac{r_{A}}{r_{B}} α_{A} = \frac{10}{25} \times \frac{π}{2} = \frac{π}{5} r a d / s^{2}$
$ω_{B} = \frac{2 π \times 100}{60} = \frac{10 π}{3} r a d / s$
$ω_{B} = ω_{B O} + α_{B} t$
$\frac{10 π}{3} = 0 + \frac{π}{5} t \Rightarrow t = \frac{50}{3} sec$

|

Updated on:21/07/2023

Class 11 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A wheel having radius 10 cm is coupled by a belt to another wheel of radius 30 cm . 1st wheel increases its angular speed from rest at a uniform rate of $1.5 {rads}^{- 2}$ . The time for 2nd wheel to reach a rotational speed of 100rev/min is ... (assume that the belt does not slip )
A20 sec
B10 sec
C $1.5$ sec
D15sec
Question 2 - Select One
In figure whell $A$ of radius $r_{A} = 10 c m$ is coupled by belt $B$ to whell $C$ of radius $r_{C} = 25 c m$ . The angular speed of whell $A$ is increased from rest at a constant rate of $1.6 r a d / s^{2}$ . Find the time needed for whell $C$ to reach an angular speed of $12.8 r a d / s$ , assuming the belt does not slip.
.
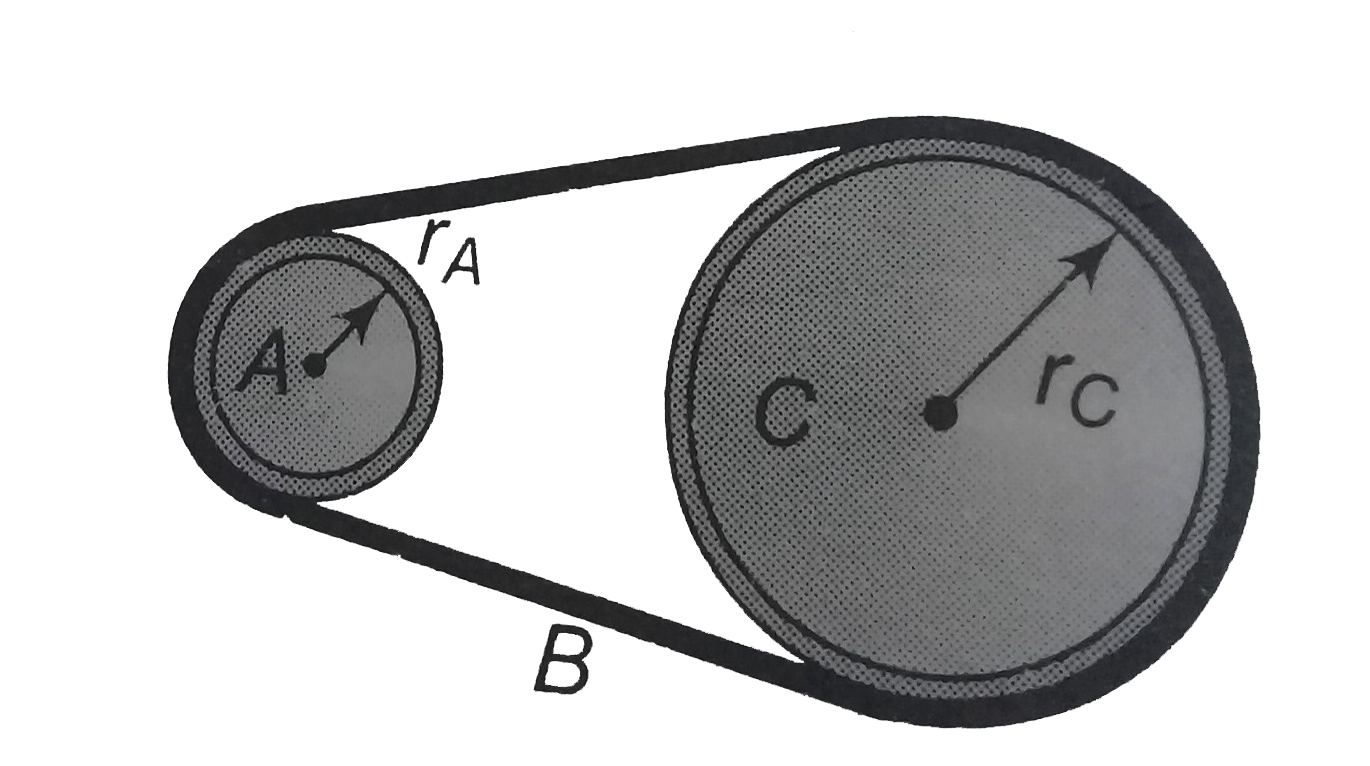A15 s
B12.5 s
C20 s
D10 s
Question 3 - Select One
A belt passes over a wheel of radius 25 cm. If a point on the belt has a speed of $5 m / s$ , the belt is moving with an angular velocity of
A $3.2 r a d / s$
B $0.32 r a d / s$
C $20 r a d / s$
D $0.032 r a d / s$

RESONANCE-DAILY PRACTICE PROBLEMS-dpp 69

Home
Ask Doubt
Profile