Two wheels are connected by a belt. The radius of larger wheel is three times that of the smaller one . What is the ratio of the rational inertia of larger wheel to the smaller wheel , when both wheels to the same angular momentum ?
3
6
9
12
The correct Answer is:A
To solve the problem, we need to find the ratio of the moment of inertia of the larger wheel to that of the smaller wheel, given that both wheels have the same angular momentum.
1. Define the Variables:
- Let the radius of the smaller wheel be R1.
- Then, the radius of the larger wheel R2=3R1.
2. Angular Momentum Relationship:
- The angular momentum L of a rotating object is given by the formula:
L=Iω
where I is the moment of inertia and ω is the angular velocity.
3. Set Up the Angular Momentum Equations:
- For the smaller wheel:
L1=I1ω1
- For the larger wheel:
L2=I2ω2
- Given that L1=L2, we have:
I1ω1=I2ω2
4. Relate Angular Velocities:
- The linear velocities at the edges of both wheels must be equal since they are connected by a belt. Therefore:
V1=V2
- This gives us:
ω1R1=ω2R2
- Substituting R2=3R1:
ω1R1=ω2(3R1)
- Simplifying this, we find:
ω1=3ω2
5. Substitute Angular Velocities into Angular Momentum Equation:
- Now substituting ω1 into the angular momentum equation:
I1(3ω2)=I2ω2
- Dividing both sides by ω2 (assuming ω2≠0):
3I1=I2
6. Find the Ratio of Moments of Inertia:
- Rearranging gives us:
I2I1=3
Final Answer:
The ratio of the moment of inertia of the larger wheel to that of the smaller wheel is:
I2I1=3
- Let the radius of the smaller wheel be R1.
- Then, the radius of the larger wheel R2=3R1.
- The angular momentum L of a rotating object is given by the formula:
L=Iω
where I is the moment of inertia and ω is the angular velocity.
- For the smaller wheel:
L1=I1ω1
- For the larger wheel:
L2=I2ω2
- Given that L1=L2, we have:
I1ω1=I2ω2
- The linear velocities at the edges of both wheels must be equal since they are connected by a belt. Therefore:
V1=V2
- This gives us:
ω1R1=ω2R2
- Substituting R2=3R1:
ω1R1=ω2(3R1)
- Simplifying this, we find:
ω1=3ω2
- Now substituting ω1 into the angular momentum equation:
I1(3ω2)=I2ω2
- Dividing both sides by ω2 (assuming ω2≠0):
3I1=I2
- Rearranging gives us:
I2I1=3
The ratio of the moment of inertia of the larger wheel to that of the smaller wheel is:
I2I1=3
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EXERCISE - III
43 Videos
- SYSTEM OF PARTICLESBOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - Level-VI
78 Videos
- THERMAL PROPERTIES OF MATTERBOOK - NARAYNACHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - LEVEL - II (H.W.)
19 Videos
Similar Questions
Knowledge Check
Two wheels are connected by a belt. The radius of the larger wheel is three times that of the smaller one. What is the ratio of the moment of inertia of larger wheel to the smaller wheel, when both wheels have same angular momentum?
A3B6C9D12Two wheels of radii 10 cm and 30 cm are connected to each other by a belt. What is the ratio of the moment of inertia of the larger wheel to that of the smaller wheel, when both of them have the same angular momentum?
A2B3C4D5Wheels A and B in Figure are connected by a belt that does not slip. The radius of B is 3.00 times the radius of A. What would be the ratio of the rotational inertias IA/IB if the two wheels had same angular momentum about their central axes.
 .A34B23C13D12
.A34B23C13D12
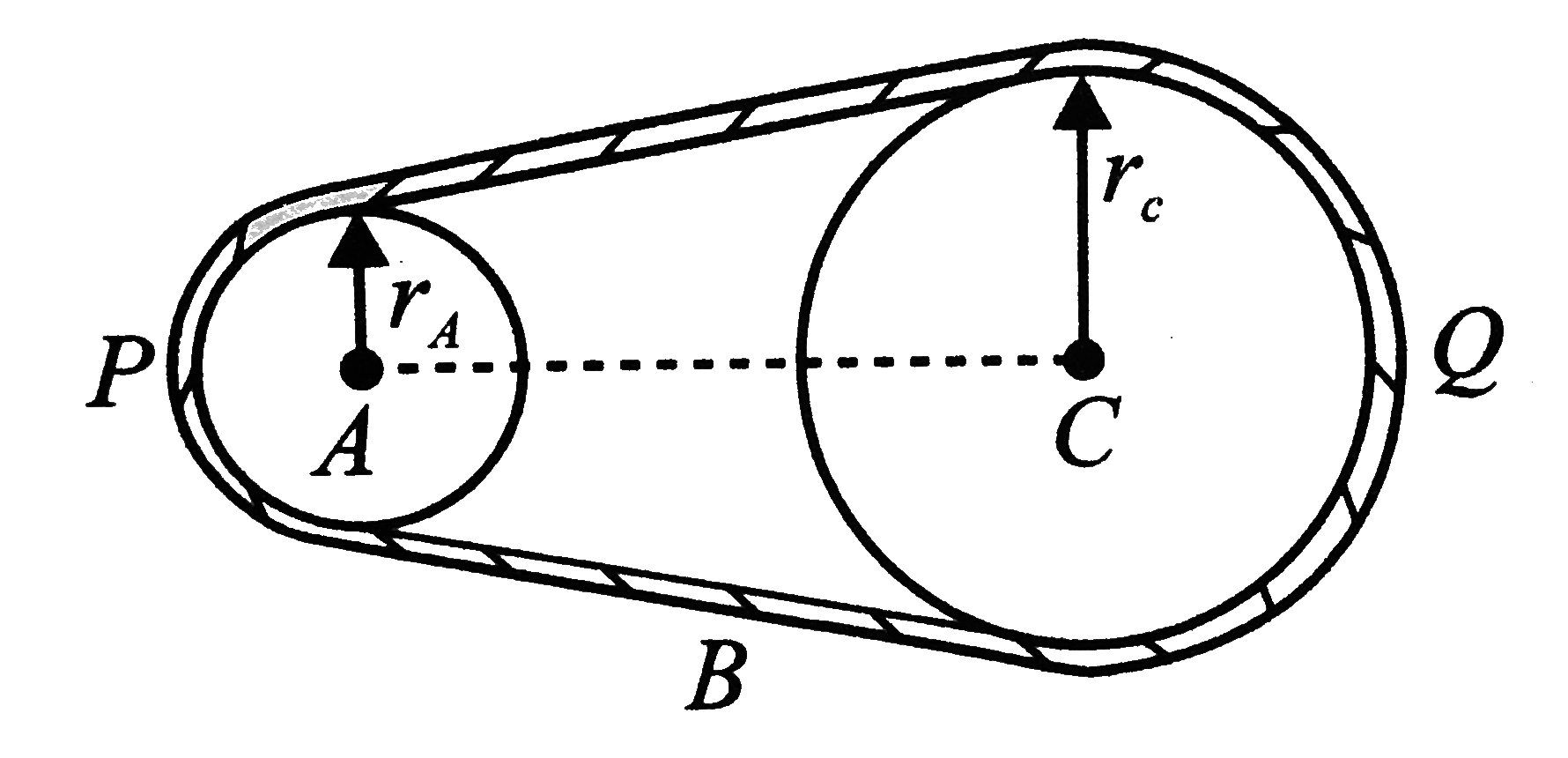
Two wheels A and C are connected by a belt B as shown in figure. The radius of C is three times the radius of A. What would be the ratio of the rotational inertias (IC/IA) if both the wheels have the same rotational kinetic energy?
View SolutionThe radius of the wheel of a wheel and axle is 4 times the radius of the axle. What is the mechanical advantage of the wheel and axle?
View SolutionA wheel travels a distance of 22 km in 2500 revolutions. What is the diameter of the wheel?
View Solutionthe radus if the rear wheel of bicycle is twice that of the front wheel. When the bicycle is moving . The angular speed of the rear wheel compared to that of the front is
View SolutionA wheel covers a distance of 1,100 cm in one round. The radius of the wheel is :
View Solution