In the figure PQRS is a frictionless horizontal plane on which a particle A of mass m moves in a circle of radius r with an angular velocity ω such that ω2r=g/3 .Another particle of mass m is tied to A through an inextensible massless string. O is the hole through which string passes down to B. B can move only vertically. The tension in the string at this instant will be :

mg/3
2mg/3
mg/6
none
The correct Answer is:B
T−mw2r=ma
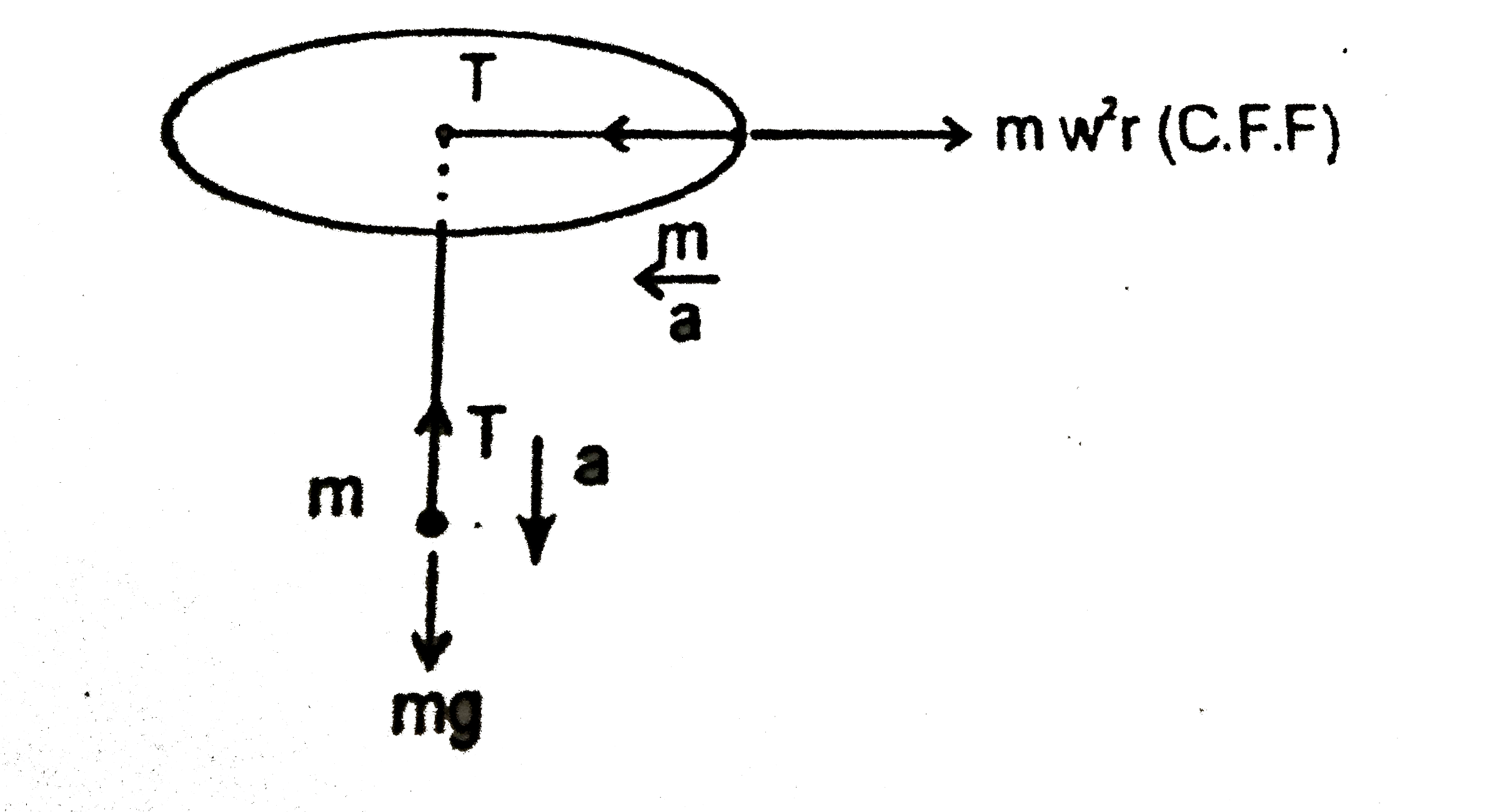
T−m(g3)=ma→(1)
mg−T=ma→(2)T−mg3=mg−T
⇒2T=4mg/3
⇒T=2mg/3Ans.(B)
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 51
7 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 52
7 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 49
6 Videos
- CURRENT ELECTRICITYBOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise
54 Videos
- ELASTICITY AND VISCOCITYBOOK - RESONANCECHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems
9 Videos
Similar Questions
Two masses ,each equal to m ,are arrached to one another by a massless string passing over a smooth pulley the tension in the string is :
View SolutionA particle of mass m attached to an inextensible light string is moving in a vertical circle of radius r. The critical velocity at the highest point is v0 to complete the vertical circle. The tension in the string when it becomes horizontal is
View Solution
Knowledge Check
Centripetal acceleration of a particle of mass m moving in a circle of radius r is 4/r2. What is the angular momentum of the particle ?
A4 m/rB4m/√rC2m√rD2 m/rA stone of mass M is tied at the end of a string, is moving in a circle of radius R, with a constant angular velocity ω. The total work done on the stone, in any half circle, is:
AπMR2ω2B2MR2ω2CMR2ω2D0A particle of mass m is tied to a string of length L and whirled into a horizontal plan. If tension in the string is T then the speed of the particle will be :
A√TlmB√2TlmC√3TlmD√Tml
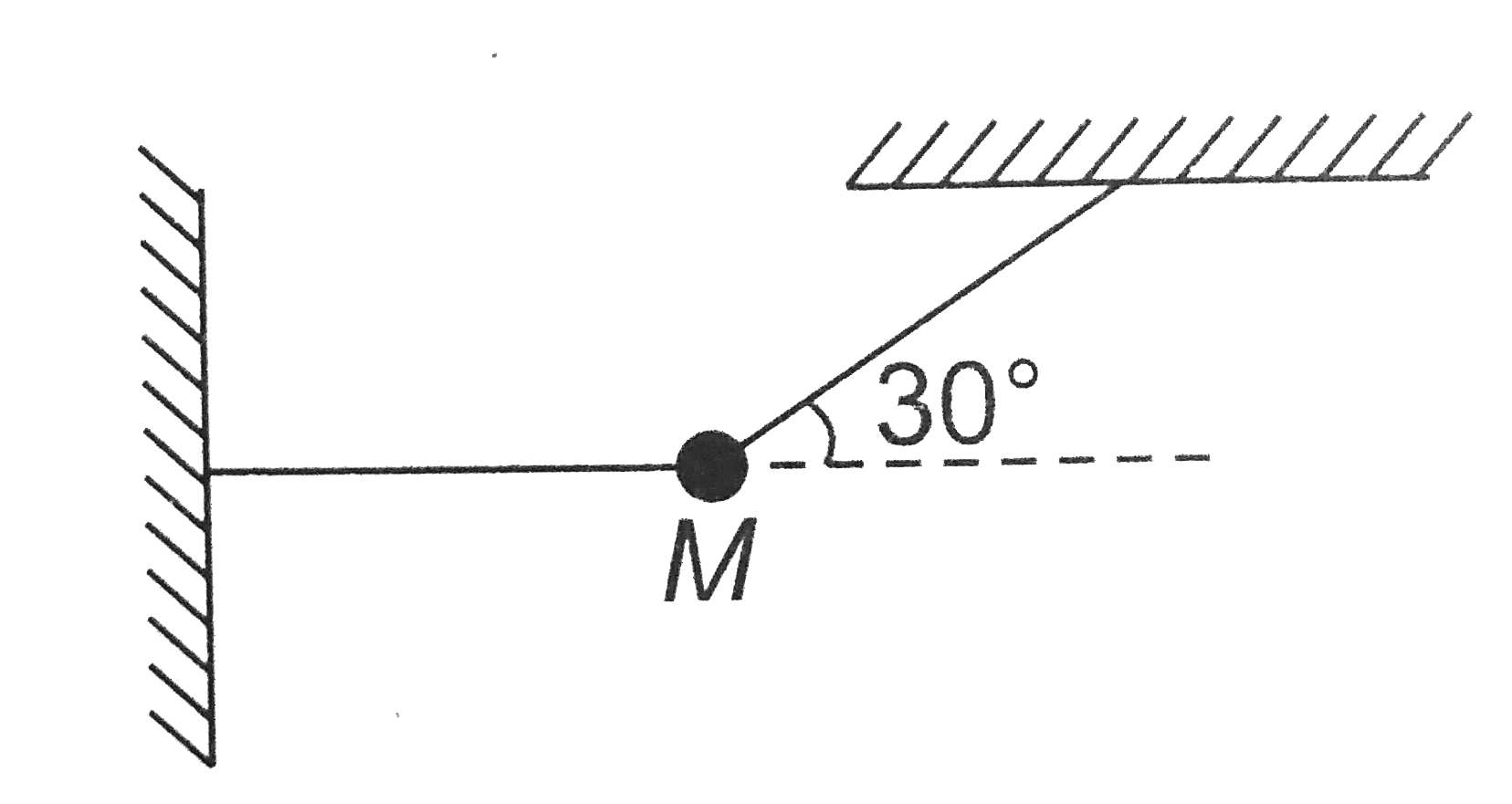
A mass M is hung with a light inextensible string. Tension in horizontal part of string is.
View SolutionA body of mass m is rotated in a vertical circle of radius R by means of light string. If the velocity of body is √gR while it is crossing highest point of vertical circle then the tension in the string at that instant is
View SolutionA particle moves in a circle of radius r with angular velocity ω. At some instant its velocity is v radius vector with respect to centre of the circel is r.At this particular instant centripetal acceleration ac of the particle would be
View SolutionA point mass m is moved in vertical circle of radius r with help of string. Velocity of mass is 7gr√ at lowest point. Tension in string at lowest point is
View SolutionA paricle of mass m is tied to a light string of length L and moving in a horizontal circle of radius r with speed v as shown. The forces acting on the particle are

View Solution