Consider the system shown below, with two equal masses m and a spring with spring constant K. The coefficient of friction between the left mass and horizontal table is μ=1/4, and the pulley is frictionless. The spring connecting both the blocks is massless and inelastic. The system is held with the spring at its unstretched length and then released.

The minimum value of μ for which the system remains at rest once it has stopped for the first time is
1√3
13
12
1√2
The correct Answer is:B
When the masses are stopped at this value of x, the forces on left mass for it to remain at rest is zero

⇒kx=mg+f
⇒k2mgk(1−μ)≤mg+μmg
∴Mu≥1/3∴least value of μ is 1/3.
Similar Questions
Two blocks of Masses M and 2M are connected by a spring of stiffness k .The coefficient of friction between the blocks and the surface is mu Find the minimum constant force F to be applied to 2m in order to slide the mass M .
View SolutionA block of mass m is connected to a massless pulley and mass-less spring of stiffness k. The pulley is frictionless. The string is mass-less. Initially the spring is unstretched when the block is released. When the spring is maximum stretched, find the ratio of tenstion in the rope and weight of the block.

View Solution
Knowledge Check
Consider the system shown below, with two equal masses m and a spring with spring constant K. The coefficient of friction between the left mass and horizontal table is μ=1/4, and the pulley is frictionless. The spring connecting both the blocks is massless and inelastic. The system is held with the spring at its unstretched length and then released.
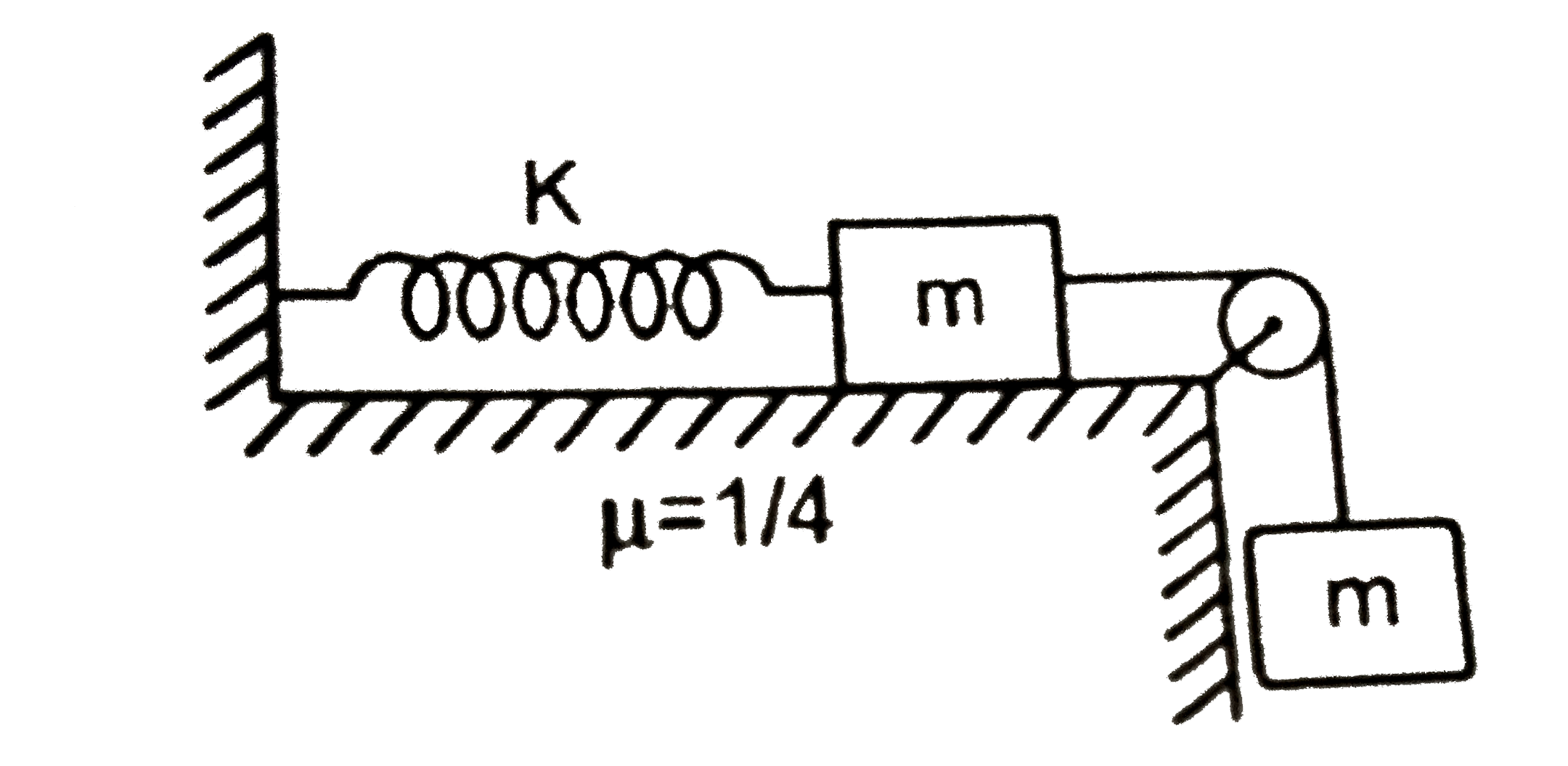
The extension in spring when the masses come to momentary rest for the first time isA3mg2KBmg2KCmgKD2mgKConsider the system shown below, with two equal masses m and a spring with spring constant K. The coefficient of friction between the left mass and horizontal table is μ=1/4, and the pulley is frictionless. The spring connecting both the blocks is massless and inelastic. The system is held with the spring at its unstretched length and then released.
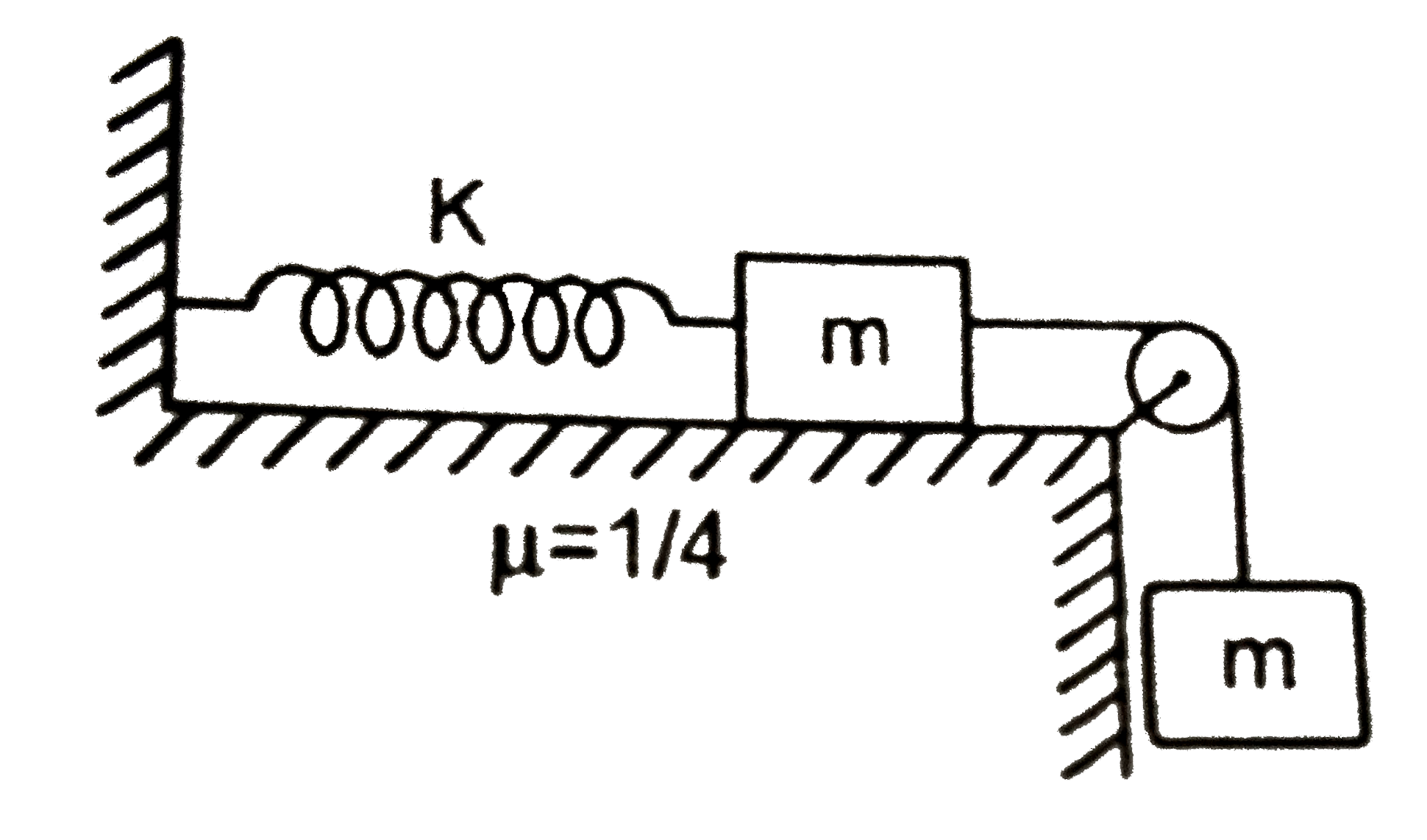
If the string connecting both the masses is cut just at the instant both masses came to momentary rest for the first time in question 5, then maximum compression of spring during resulting motion is (Take μ=1/4)A2mg3KBmg2KCmgKD1mg3KIn the system as shown in figure, the blocks have masses m1 and m2, the spring constant is k, coefficient of friction between the block of mass m1 and the surface is μ. The system is released with zero initial speed from the position where the spring is in its natural length.
 AThe maximum possible speed of the blocks is g(m2−μm1)√k(m1+m2)BThe maximum possible speed of the blocks is g(μm1)√k(m1+m2)CThe maximum possible speed of the blocks if friction is absent is gm2√k(m1+m2)DThe maximum possible speed of the blocks if friction is absent is gm1√k(m1+m2)
AThe maximum possible speed of the blocks is g(m2−μm1)√k(m1+m2)BThe maximum possible speed of the blocks is g(μm1)√k(m1+m2)CThe maximum possible speed of the blocks if friction is absent is gm2√k(m1+m2)DThe maximum possible speed of the blocks if friction is absent is gm1√k(m1+m2)
The block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.

View SolutionAn ideal spring with spring constant k is hung from the ceiling and a block of mass M is attached to its lower end. The mass is released with the spring initially unstretched. Then the maximum extension in the spring is
View SolutionTwo blocks of mass m1 and m2, resting on a frictionless table, are connected by a stretched spring and then released -
View SolutionA block of mass 2M is attached to a massless spring with spring-constant k. This block is connected to two other blocks of masses M and 2M using two massless pulleys and strings. The accelerations of the blocks are a1a2 and a3 as shown in the figure. The system is released from rest with the spring in its unstretched state. The maximum extension of the spring is x0 Which of the following option(s) is(are) correct? [g is the acceleration due to gravity. Neglect friction]
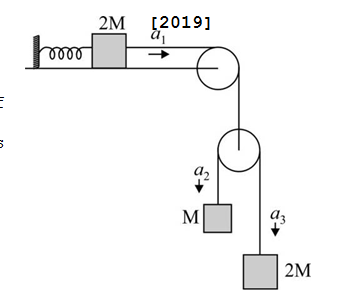
View SolutionConsider the condition shown in the figure. Pulley is massless and frictionless, springs are massless. Both the blocks are released with the springs in their natural lengths. Choose the correct options.
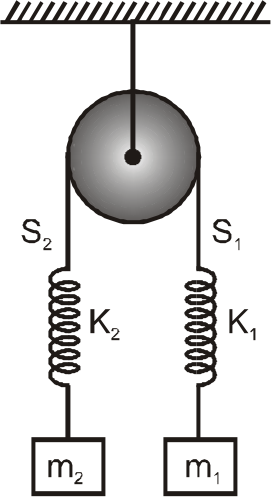
View Solution
