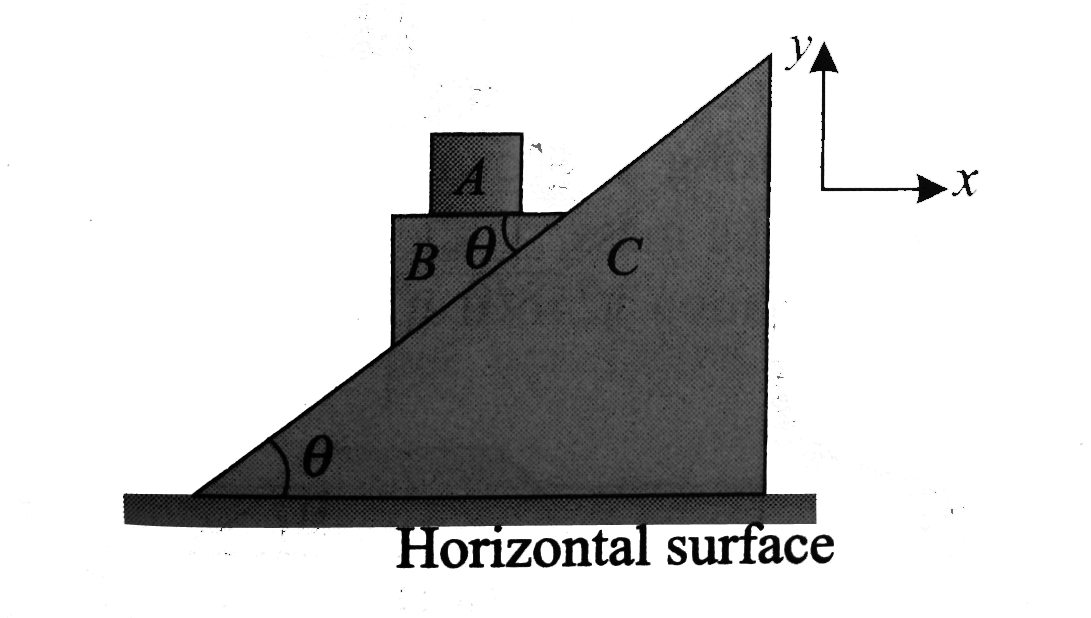
In the figure shown all the surface are smooth. All the blocks A,B and C are movable x-axis is horizontal and y-axis vertical as shown. Just after the system is relased from the position as shown.
Acceleration of 'A' relative to ground is in negative y− direction
Acceleration of 'A' relative to B is in positive x− direction
The horizontal acceleration of 'B' relative to ground is in negative x− direction.
The acceleration of 'B' relative to ground directed along the inclined surface of 'C' is greater than gsinθ.
The correct Answer is:A, B, C, D
There is no horizontal force on block A, therefore it does not move in x− directing , whereas there is net downward force (mg−N) is acting on it, making its acceleration along negative y− direction. Block B moves downward as well as in negative x− direction. Downward acceleration of A and B will be equal due to constrain, thus w.r.t.B,A moves in positive x− direction.
Due to the component of normal exerted by C on B, it moves inn negative x− direction.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp29
5 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 30
4 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 27
3 Videos
- CURRENT ELECTRICITYBOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise
54 Videos
- ELASTICITY AND VISCOCITYBOOK - RESONANCECHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems
9 Videos
Similar Questions
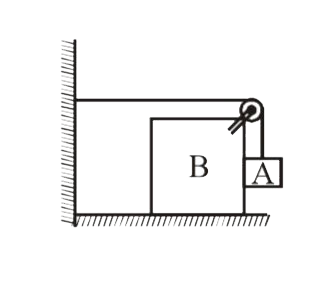
In the system shown in the diagram all surfaces are smooth, pulley and strings are ideal. If −→aA and −→aB are the accelerations of the two blocks, then just after the system is released from rest, then choose correct statement(s) :
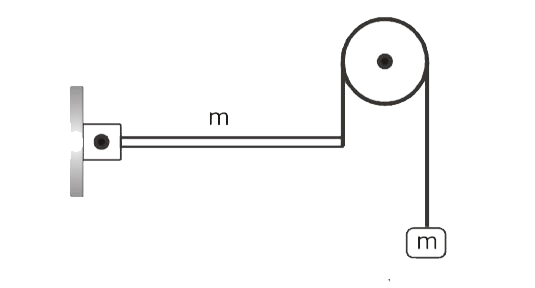
View SolutionA rod and a block are of same mass. Initially rod is in horizontal position. What will be acceleration of tip of the rod just after the system is released from this position shown in figure.
View Solution
Knowledge Check
In the figure shown all the surface are smooth. All the blocks A, B and C are movable, x-axis is horizontal and y-axis verticle as shown. Just after the system is released from the position as shown.
 AAcceleration of 'A' relative to ground is in negative y-directionBAcceleration of 'A' relative to B is in positive x-directionCThe horizontal acceleration of 'B' relative to ground is in negative x-directionDThe acceleration of 'C' relative to 'B' is directed along the inclined surface
AAcceleration of 'A' relative to ground is in negative y-directionBAcceleration of 'A' relative to B is in positive x-directionCThe horizontal acceleration of 'B' relative to ground is in negative x-directionDThe acceleration of 'C' relative to 'B' is directed along the inclined surfaceIn the figure shown A and B are free to move . All the surface are smooth. Mass of Aism. Then
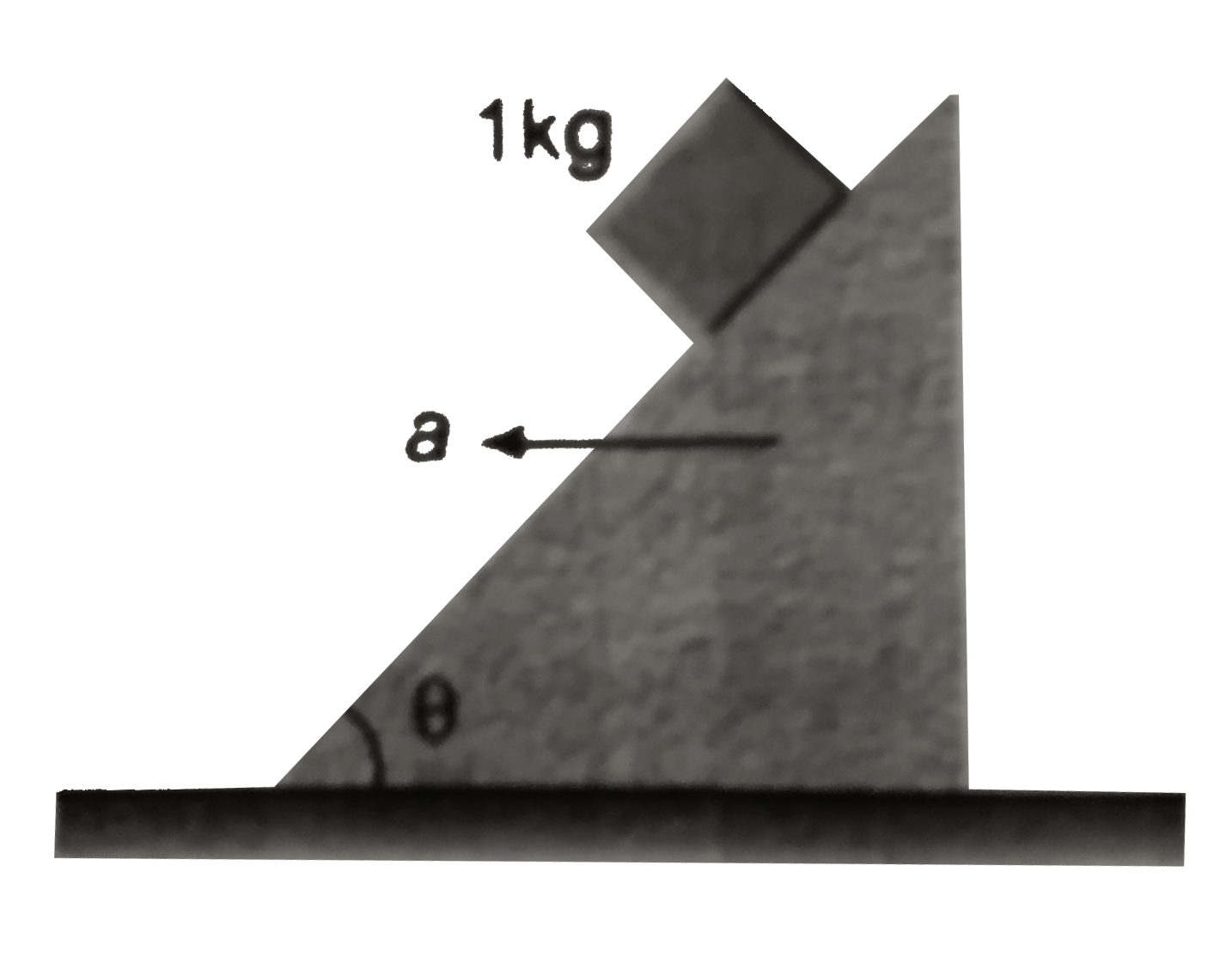 Athe acceleration of A will be more than gsinθBthe acceleration of A will be less than gsinθCnormal reation A due to B will be more than mgcosθDnormal reation A due to B will be less than mgcosθ
Athe acceleration of A will be more than gsinθBthe acceleration of A will be less than gsinθCnormal reation A due to B will be more than mgcosθDnormal reation A due to B will be less than mgcosθIn the figure shown, all the surfaces are rough. Both the blocks have the same mass. The friction coefficient between all the surface is the same. Choose the correct statements.
 AIf friction between A and B is kinetic, friction between A and ground is also kineticBIf friction between A and B is Static, friction between A and ground is also staticCIf friction between A and B is kinetic, friction between A and ground is staticDIf friction between A and B is staic, friction between A and ground is kinetic
AIf friction between A and B is kinetic, friction between A and ground is also kineticBIf friction between A and B is Static, friction between A and ground is also staticCIf friction between A and B is kinetic, friction between A and ground is staticDIf friction between A and B is staic, friction between A and ground is kinetic
In the figure shown , all surface are smooth . Acceleration of mass '4m' , when the system Is released from rest will be

View SolutionIn the shown figure, if all the surface are smooth and the two masses are allowed to move then center of mass of the system will move
View SolutionIn the system shown in figure, all surfaces are smooth, pulley and strings are massless. Mass of both A and B are equal. The system is released from rest.

(a) Find the →aA.→aB immediately after the system is released. →aAand→aB are accelerations of block A and B respectively.
(b) Find →aA immediately after the system is released.
View SolutionIn the figure shown , A and B are free of to move. All the surfaces are smooth. (0<θ<90∘)

View SolutionAll the surfaces are smooth as shown in figure. The acceleration of mass m relative to wedge is :

View Solution
