A block B of mass 0.6kg slides down the smooth face PR of a wedge A of mass 1.7kg which can move freely on a smooth horizontal surface.
The inclination of the face PR to the horizontal is 45∘ . Then :

the acceleration of A is 3g/20
the vertical component of the acceleration of B is 23g/40
the horizontal component of the acceleration of B is 17g/40
none of these
The correct Answer is:A, B, C
F.B.D. of block Bw.r.t. wedge
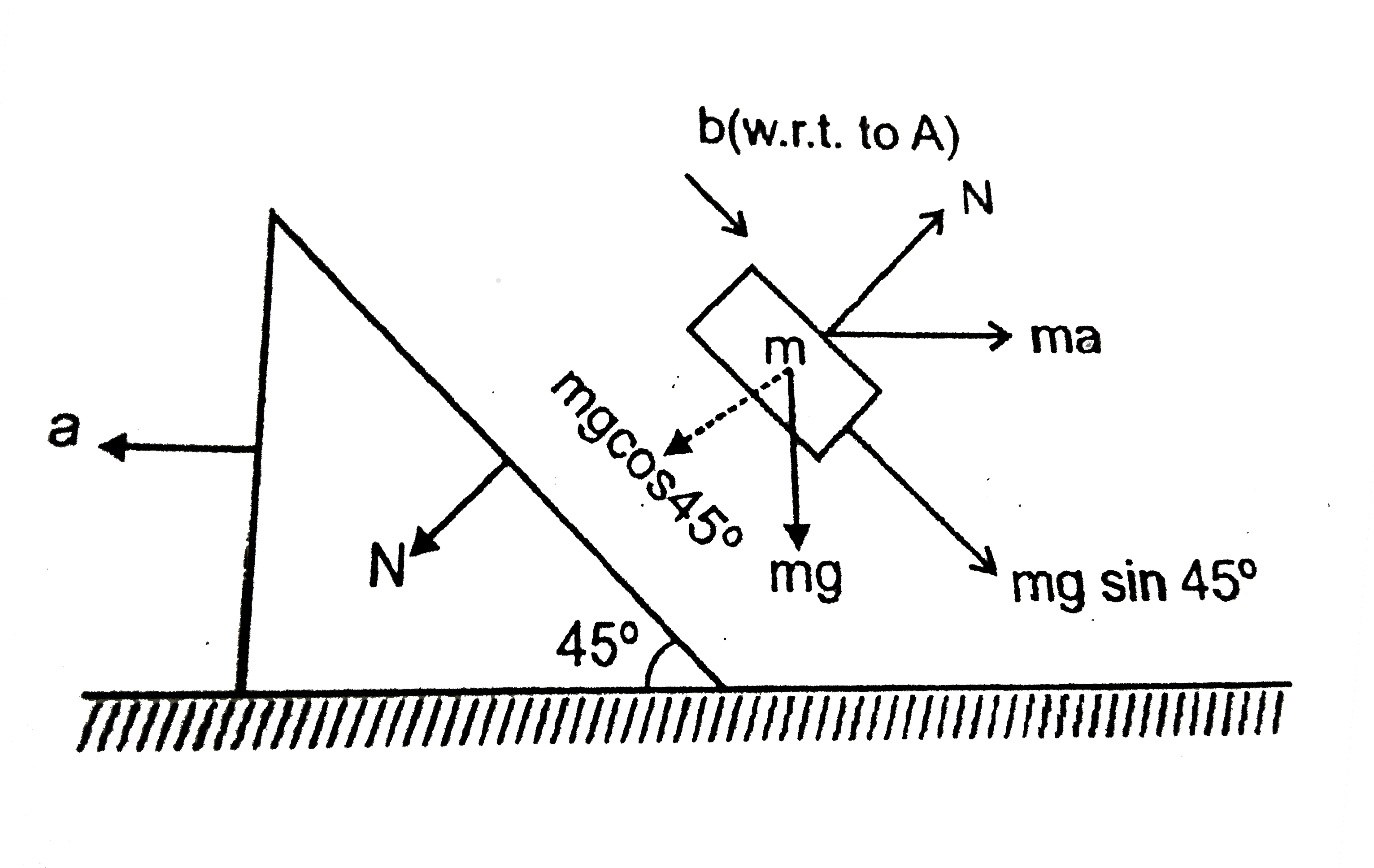
for block A ltbr> Ncos45∘=1.7a….(1)
for block B
0.6gsin45∘=0.6acos45∘=0.6b…..(b)
N+0.6acos45∘=0.6gcos45∘….(ii)
by solving (i),(ii)&(iii)
a=3g20 and b=23g20√2
Now vertical component acceleration of
B=bcos45∘=23g40
and horizontal component of acceleration of
B=bsin45∘−a=17g40
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp29
5 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 30
4 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 27
3 Videos
- CURRENT ELECTRICITYBOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise
54 Videos
- ELASTICITY AND VISCOCITYBOOK - RESONANCECHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems
9 Videos
Similar Questions
A block of mass m is placed at rest on a smooth wedge of mass M placed at rest on a smooth horizontal surface. As the system is released

View SolutionA block of mass m slides over a smooth wedge of mass M which is placed over a rough horizontal surface . The centre of mass of the system will move towards left

Here μ = coefficient of friction between the wedge and the ground .
View Solution
Knowledge Check
A block of mass m rests on a stationary wedge of mass M. The wedge can slide freely on a smooth horizontal surface as shown in figure. If the block starts from rest
 A(a) the position of the centre of mass of the system will changeB(b) the position of centre of mass of the system will change along the vertical but not along the horizontalC(c) the total energy of the system will remain constantD(d) All of the above
A(a) the position of the centre of mass of the system will changeB(b) the position of centre of mass of the system will change along the vertical but not along the horizontalC(c) the total energy of the system will remain constantD(d) All of the aboveA block of mass 2kg slides down the face of a smooth 45∘ wedge of mass 9kg as shown in the figure. The wedge is placed on a frictionless horizontal surface. Determine the acceleration of the wedge.
 A2ms−2B11√2ms−2C1ms−2Dnone of these
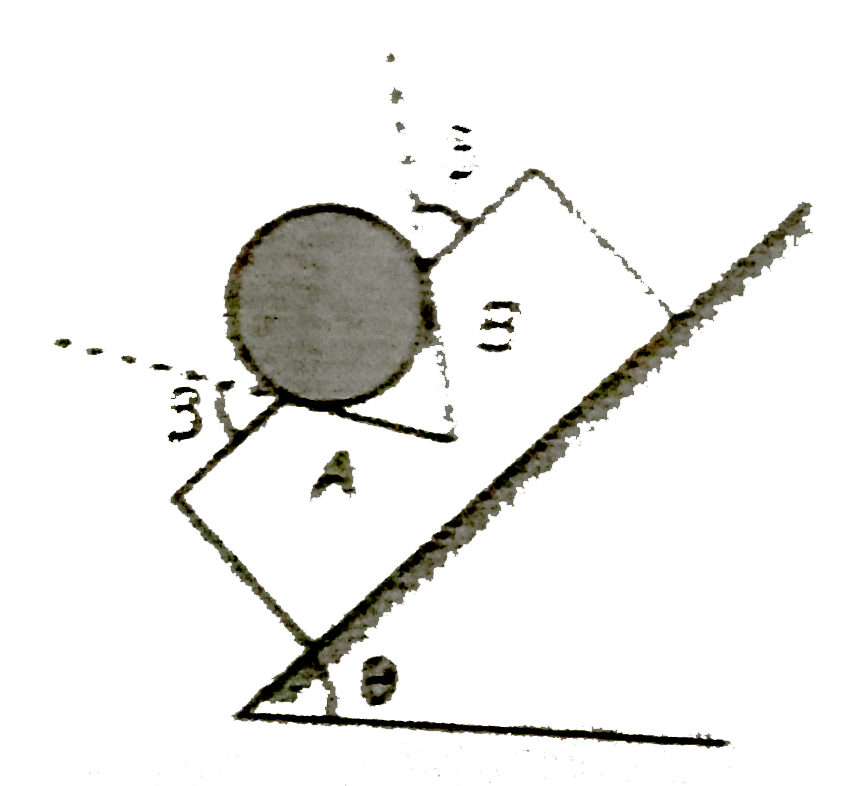
A2ms−2B11√2ms−2C1ms−2Dnone of theseA small block of mass m is placed at rest on the top of a smooth wedge of mass M, which in turn is placed at rest on a smooth horizontal surface as shown in figure. It h be the height of wedge and θ is the inclination, then the distance moved by the wedge as the block reaches the foot of the wedge is
 AMhcotθM+mB(b) mhcotθM+mC(c) MhcosecθM+mD(d) mhcosecθM+m
AMhcotθM+mB(b) mhcotθM+mC(c) MhcosecθM+mD(d) mhcosecθM+m
Block A of mass 1kg is placed on the rough surface of block B of mass 3kg. Block B is placed on smooth horizontal surface. Blocks are given the velocities as shown. Find net work done by the frictional force. [in (−)veJ].
 .
.
View SolutionA block of mass 2 kg is kept on a smooth wedge of mass 3 kg and wedge is kept on a rough horizontal surface. A vertical force of 60 N is applied on the minimum coefficient of friction between the wedge and horizontal surface, so that wedge remains at rest during the motion of block on the wedge ?
View SolutionA block A of mass 2kg is placed over smooth block B of mass 4kg which is placed over a smooth horizontal floor The coefficient of friction between A and B is 0.4 when a horizontal forces of magnitude 10N is applied on A the acceleration of block of A and B are

View SolutionA trolley containing a liquid slides down a smooth inclined plane of angle α with the horizontal. Find the angle of inclination θ of the free surface with the horizontal.

View SolutionA force of 50N acts in the direction as shown in figure. The block of mass 5kg, resting on a smooth horizontal surface. Find out the acceleration of the block.
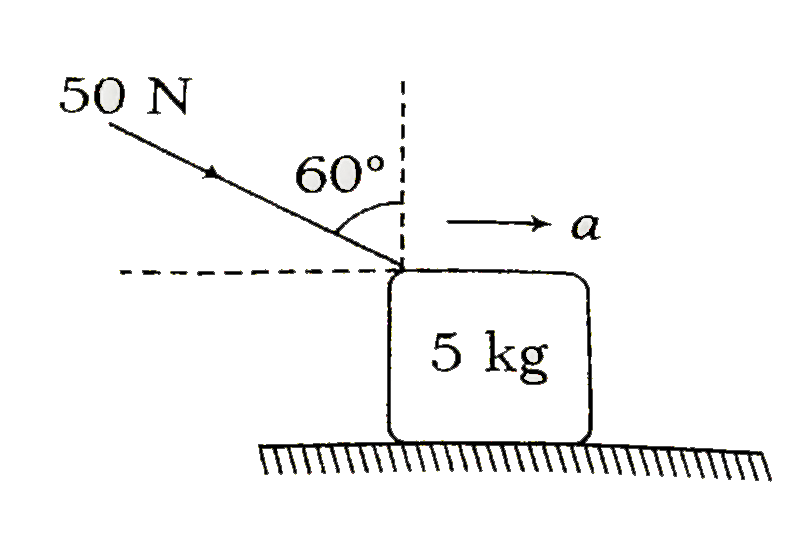
View Solution
