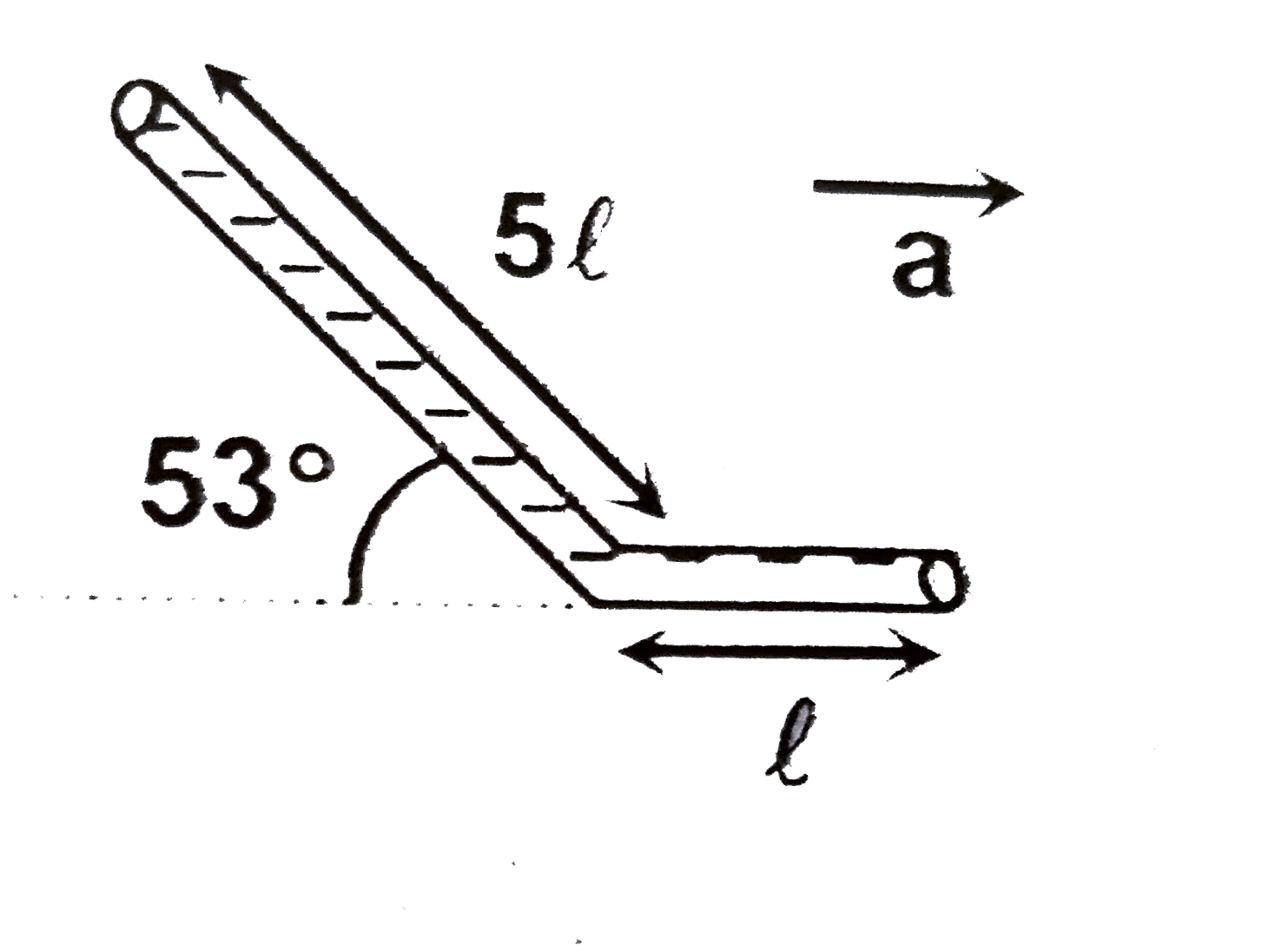
In the given tube liquid density ρ is filled. Find the acceleration of the tuve towards right direction such that no liquid will fall out of the tube.
35g
45g
g
4g
The correct Answer is:C
tanθ=4l4l=ag
⇒a=g
Or, PA−P0A=(ρlA)a
(5l)(ρA)(g45−35a)=ρlρa
a=g

Topper's Solved these Questions
- TEST PAPERSBOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS
747 Videos
- SIMPLE HARMONIC MOTIONBOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assignment Problems (Objective) (Level-II)
20 Videos
- WORK, ENERGY AND POWER BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - COMPREHENSIONS ( Comprehension-II)
5 Videos
Similar Questions
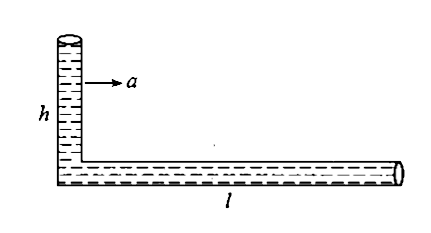
Figure shows as a L-shaped tube in which a liquid of density ρ is filled. Find with what acceleration the tube is accelerated towards right so that no liquid will fall out of the tube.
View SolutionA vertical U-tube has two liquids 1 and 2. The heights of liquids columns in both the limbs are h and 2h, as shown in the figure. If the density of the liquid 1 is 2ρ.
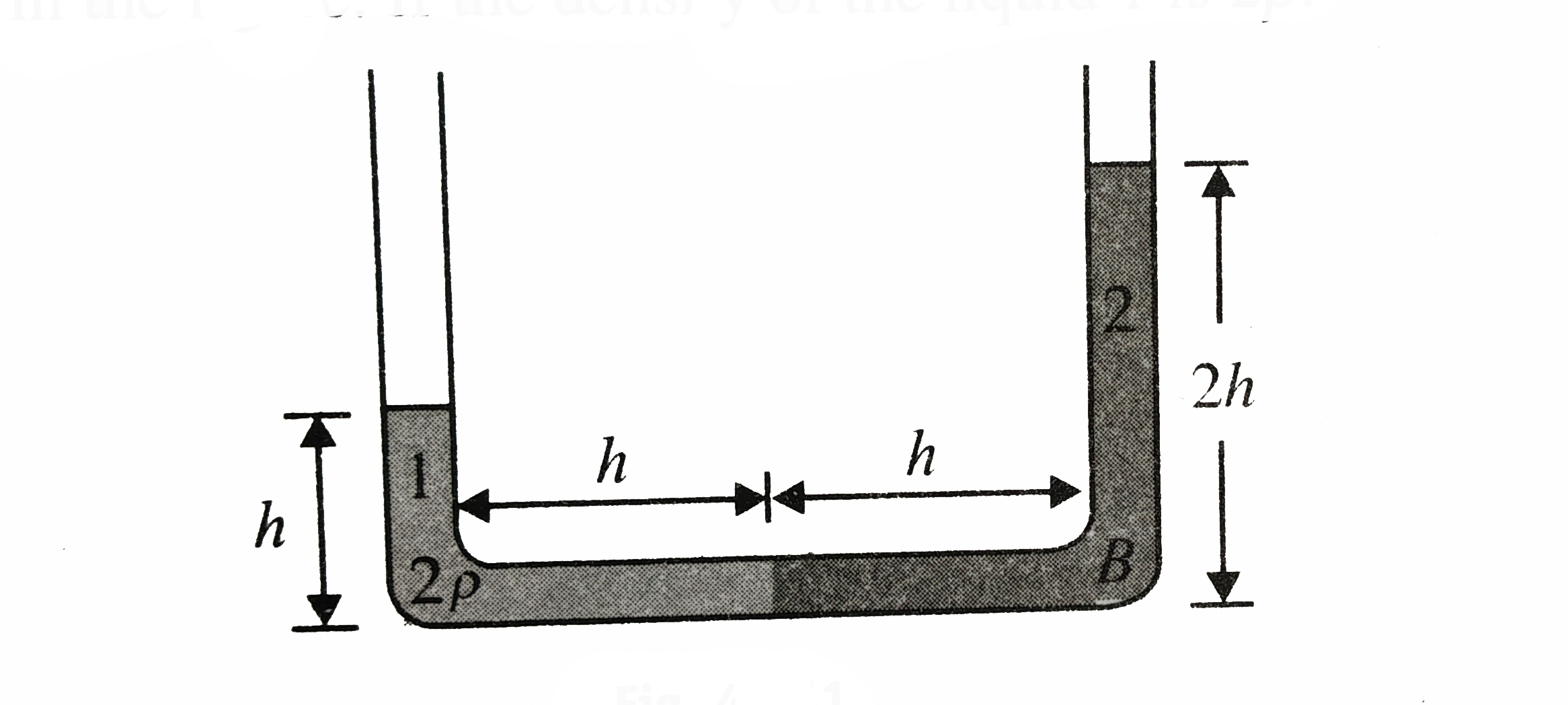
a. Find the density of liquid 2.
b. If we accelerate the tube towards right till the heights of liquid columns will be the same, find the acceleration of the tube.
View Solution
Knowledge Check
A narrow tube completely filled with a liquid is lying on a series of cylinders as shown in the figure. Assuming no sliding between any surfaces, the value of acceleration of the cylinders for which liquid will not come out of the tube from anywhere is given by
 AgH2LBgHLC2gHLDgH√2L
AgH2LBgHLC2gHLDgH√2LA liquid of density ρ is filled in a U-tube is accelerated with an acceleration a so that the height of liquid in its two vertical arms are h1andh2 as shown in the figure. If l is the length of horizontal arm of the tube, the acceleration a is
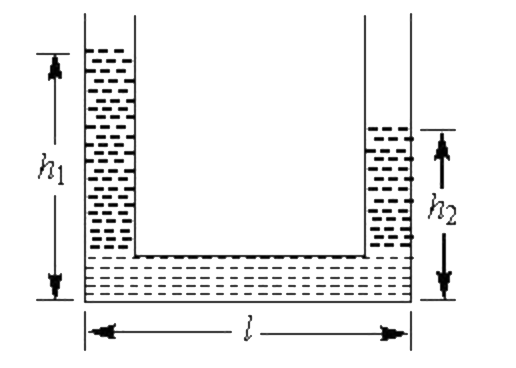 Ag(h1−h2)2l towards rightBg(h1−h2)2l towards leftCg(h1−h2)l towards rightDg(h1−h2)l towards left
Ag(h1−h2)2l towards rightBg(h1−h2)2l towards leftCg(h1−h2)l towards rightDg(h1−h2)l towards leftA block of volume V and density ρ is floating in a liquid of density 2ρ filled in a vessel. Now the vesset starts falling freely with acceleration g. Then the volume of block inside the liquid in the falling condition is
AVBV/2CarbitrayDzero
A container contains an incompressible and non - viscous liquid of density ρ and is filled upto a height H . Now if container is moved towards right with an acceleration a then find the horizontal force exerted by liquid on the face ABCD of container . Assume container have enough height so that liquid does not fall outside the container .
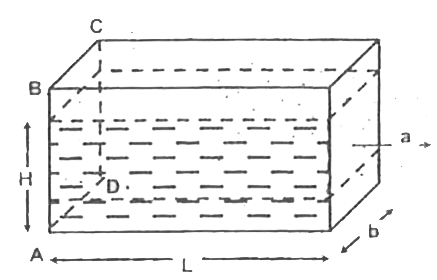
View SolutionThere is a U-tube of different cross sectional area A=2.5cm2 and 4A of limbs fitted with the frictionless pistons each of mass m= 1 kg. An ideal liquid of density ρ=2000kg/m3 is filled in the tube and the tube is accelerated in horizontal direction with a constant acceleration 'a'. Find the value of acceleration 'a' (in m/s2 ) for which both pistons stay in the same horizontal level. The length of horizontal section of U-tube is l =1 m. (Take g=10m/s2 )
View SolutionLength of a horizontal arm of U-tube is L and ends of both the vertical arms are open to atompsheric pressure P0, A liquid of density ρ is poured in the tube such that liquid just fills the horizontal part of the tube as shown in figure . Now one end of the opened ends is sealed and the tube is then rotated about a vertical axis passing through the other vertical arm with angular speed ω0. if length of each vertical arm is a and in the sealed end liquid rises to a height y, find pressure in the sealed tube during rotation.
View SolutionA container having a liquid of density ρ is moving downwards with acceleration g2. Find the pressure difference between two vertical points in the liquid separated by h
View SolutionA vertical U tube contains a liquid of density ρ, length of the liquid in the tube is 2H. The liquid is displaced slightly and released. Show that the liquid will execute SHM. Also find its time period. Take liquid to be ideal.
View Solution
