A particle of charge per unit mass α is released from origin with a velocity →v=v0ˆi in a magnetic field
→B=−B0ˆk for x≤√32v0B0α
and →B=0 for x>√32v0B0α
The x-coordinate of the particle at time t(π3B0α) would be
√32voBoα+√32vo(t−πBoα)
√32voBoα+vo(t−π3Boα)
√32voBoα+vo2(t−π3Boα)
√32voBoα+vot2
The correct Answer is:C
r=mvoBoq=voBoα
xr=√32=sinθ∴θ=60∘
toA=T6=π3Boα Therefore x− coordinate of particle at any time t>π3Boα will be
x=√32voBoα+vo(t−π3Boα)cos60∘Sox=(√32voBoα)+vo2(t−π3Boα)
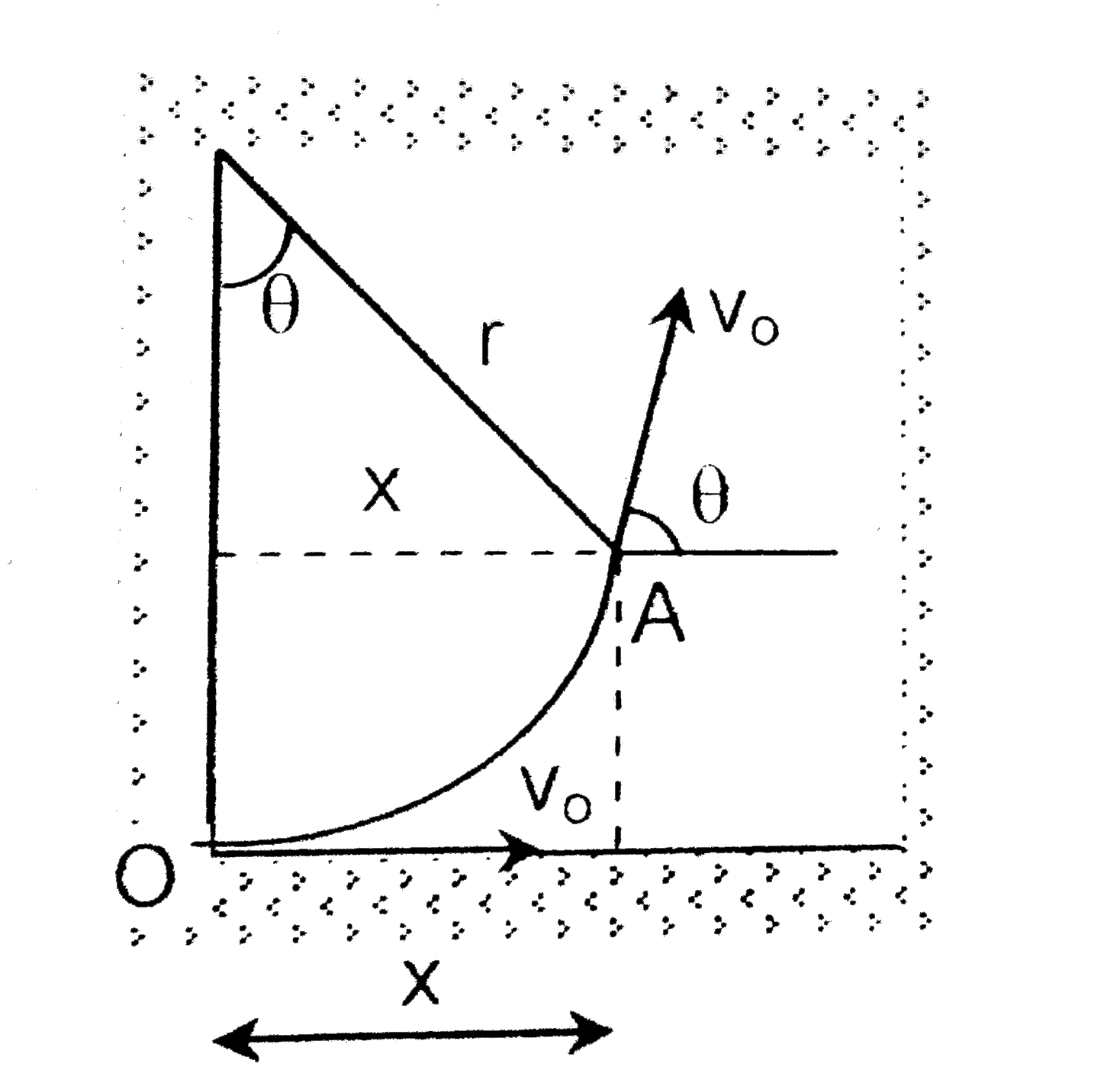
Topper's Solved these Questions
- TEST PAPERSBOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS
747 Videos
- SIMPLE HARMONIC MOTIONBOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assignment Problems (Objective) (Level-II)
20 Videos
- WORK, ENERGY AND POWER BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - COMPREHENSIONS ( Comprehension-II)
5 Videos
Similar Questions
Knowledge Check
The x -co- ordinates of the particle at time t (>π3B0α) would be
A−2V0B0αB−V0B0αC2V0B0αD−V0B0αA particle of charge per unit mass α is released from origin with velocity →v=v0ˆi in a magnetic field
→B=−B0ˆk for x≤√32v0B0α
and →B=0 for x>√32v0B0α
The x-coordinate of the particle at time t(>π3B0α) would beA√32v0B0α+√32v0(t−πB0α)B√32v0B0α+v0(t−π3B0α)C√32v0B0α+v02(t−π3B0α)D√32v0B0α+v0t2A particle of charge per unit mass α is released from origin with a velocity →v=v0ˆi uniform magnetic field →B=−B0ˆk. If the particle passes through (0,y,0), then y is equal to
A−2v0B0αBv0B0αC2v0B0αD−v0B0α
A particle of charge per unit mass α is released from origin with a velocity →v=v0ˆi in a magnetic field
→B=−B0ˆk for x≤√32v0B0α
and →B=0 for x>√32v0B0α
The x-coordinate of the particle at time t(π3B0α) would be
View SolutionA charged particle (q.m) released from origin with velocity v=v0ˆi in a uniform magnetic field B=B02ˆi+√3B02ˆJ.
Maximum z-coordinate of the particle is
View SolutionA charged particle (q.m) released from origin with velocity v=v0ˆi in a uniform magnetic field B=B02ˆi+√3B02ˆJ.
When z-co-ordinate has its maximum value
View SolutionA charged particle (q.m) released from origin with velocity v=v0ˆi in a uniform magnetic field B=B02ˆi+√3B02ˆJ.
Z-component of velocity is √3v02 after in t=……….
View SolutionAn electron is moving with an initial velocity →v=v0ˆi and is in a magnetic field →B=B0ˆj. Then it's de-Broglie wavelength
View Solution