From a sphere of electrical conductivity K two planes cut a piece such that first plane passes through the centre of sphere and second parallel to first one at distance R/2 from centre then resistance between A and B
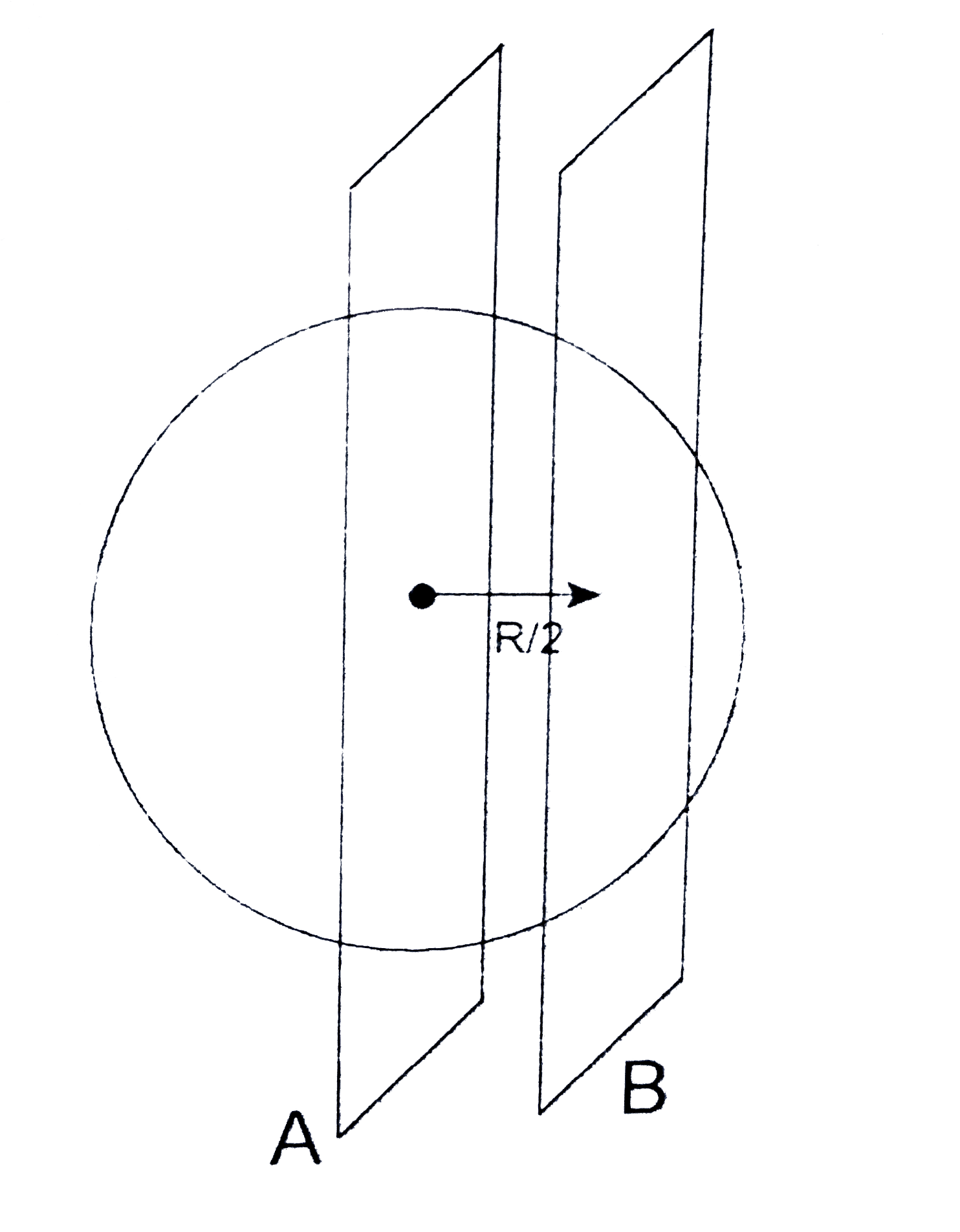
1πKR
√3πKR
ln32πKR
None
The correct Answer is:C
∫1K.dxπ(R2−x2)
RT=1kπ∫dx(R2−x2)=12KπR In (3)
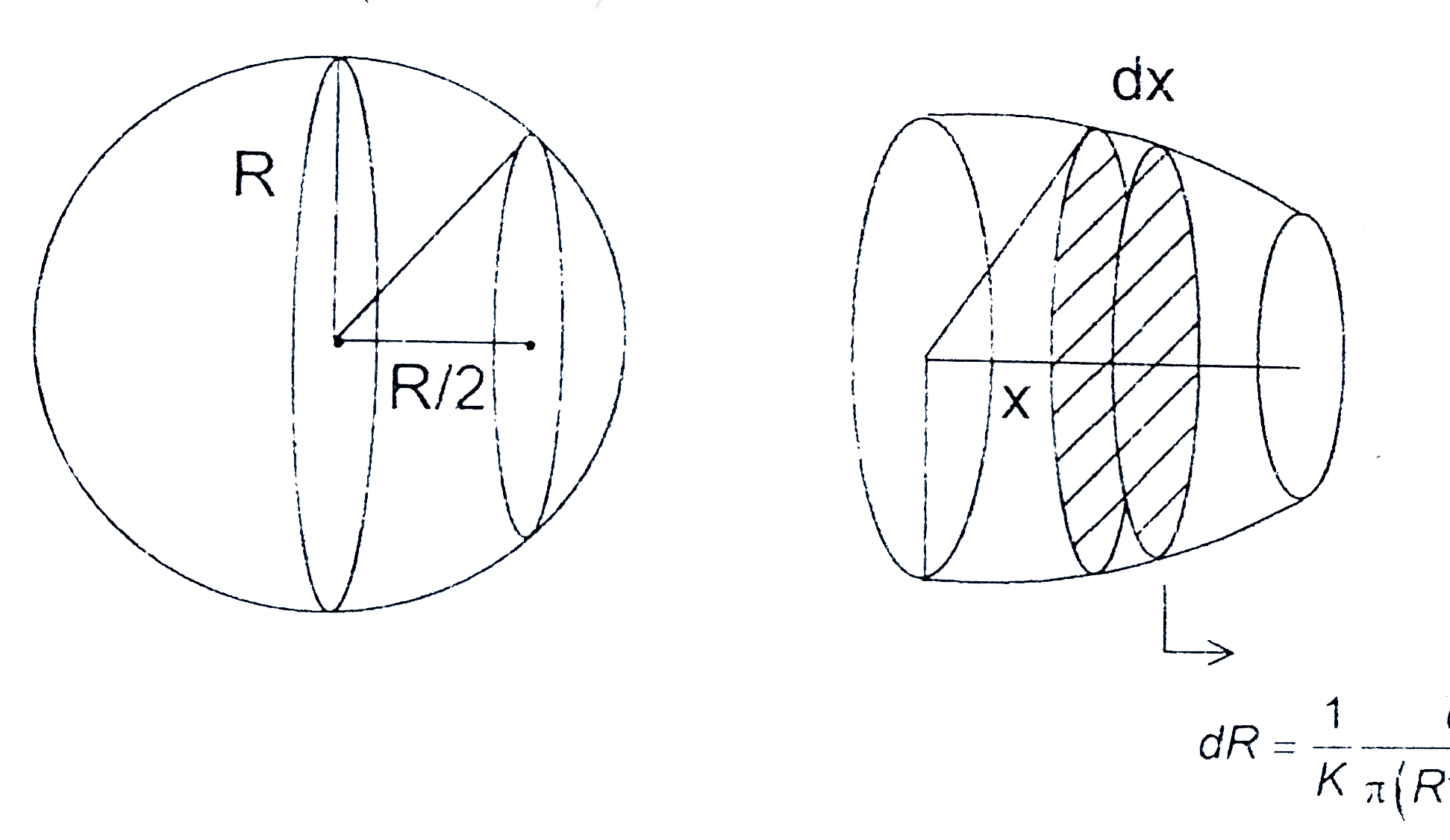
Topper's Solved these Questions
- TEST PAPERSBook:FIITJEEChapter:TEST PAPERSExercise:PHYSICS
Explore 747 Videos
- SIMPLE HARMONIC MOTIONBook:FIITJEEChapter:SIMPLE HARMONIC MOTIONExercise:Assignment Problems (Objective) (Level-II)
Explore 20 Videos
- WORK, ENERGY AND POWER Book:FIITJEEChapter:WORK, ENERGY AND POWER Exercise:COMPREHENSIONS ( Comprehension-II)
Explore 5 Videos
Similar Questions
The volume charge density of a sphere carrying charge Q and of radius R is proportional to the square of the distance from the centre. The ratio of the magnitude of the electric field at a distance 2R from the centre to that at a distance of R2 from the centre is
View SolutionA solid conducting sphere of radius r is having a charge of Q and point charge q is a distance d from the centre of sphere as shown. The electric potential at the centre of the solid sphere is :

View Solution
Knowledge Check
The electric field at a distance 3R2 from the centre of a charged conducting spherical shell of radius R is E. The electric field at a distance R2 from the centre of the sphere is :
AEB3E2CE2DZeroThe electric field at a distance 3R/2 from the centre of a charge conducting spherical shell of radius R is E. The electric field at a distance R/2 from the centre of the sphere is
AE2BzeroCEDE4The electric field at a distance 3R2 from the centre of a charged conducting spherical shell of radiu R is E. The electric field at a distance R2 from the centre of the sphere is:
AzeroBECE2DE3
The centre of neutral conducting sphere of radius "R" is at distance 'd' from a point charge "Q" .The potential of the sphere is
View SolutionA cavity of radius R/2 is made inside a solid sphere of radius R. The centre of the cavity is located at a distance R/2 from the centre of the sphere. The gravitational force on a particle of a mass 'm' at a distance R/2 from the centre of the sphere on the line joining both the centres of sphere and cavity is (opposite to the centre of cavity). [Here g=GM/R2, where M is the mass of the solid sphere]
View SolutionThe potential at a distance R/2 from the centre of a conducting sphere of radius R will be
View SolutionTwosmall neutral conducting spheres are taken and their centres are separated by a distance 2a. If n electrons are removed from one of them and deposited on the other, what is the magnitude of electric intensity due to the system at a point on the line joining the centres of the spheres and at a distance d from the midpoint of the line joining the two spheres? (e is quantum of charge)
View SolutionThere is a cubical cavity inside a conducting sphere of radius R. A positive point charge Q is placed at the centre of the cube and another positive charge q is placed at a distance 1(>R) from the centre of the sphere. The sphere is earthed
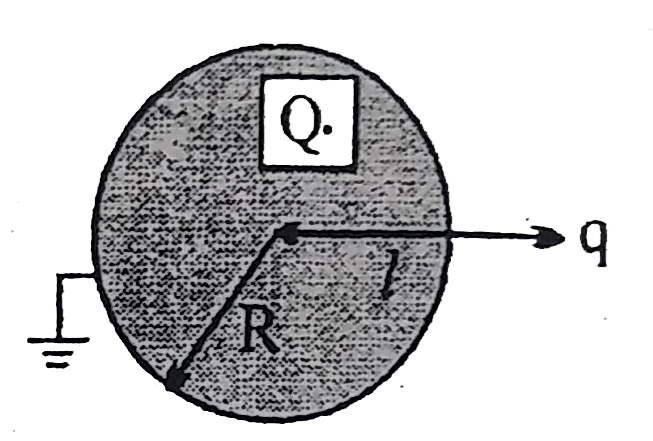
Net charge on the outer surface of conducting sphere is
View Solution

