Consider an excited hydrogen atom in state n moving with a velocity v(v<<c). It emits a photon in the direction of its motion and changes its state to a lower state m. Apply momentum and energy conservation principle to calculate the frequency v of the emitted radiation, compare this with the frequency v0 emitted if the atom were at rest.

By momentum conservation
mv=mv1+hvc
v1=v−hvmc
By energy conservation
12mv2+ΔE=12mv21+hv
" " =12m(v−hvmc)2+hv
" " =12mv2−12m.2vhvmc+12mh2v2mc+hv
ΔE=hv(1−vc){∵h2v2m2c2is negligible}
When atom is at rest
0=−mv2+hv0c
v2=hv0mc
ΔE=12mv22+hv0
=12mh2v20m2c2+hv0
hv0[∵h2v20m2c2 is negligible]
ΔE=hv0=hv(1−v/c)
v=v0(1−v/c)=v0(1−v/c)−1=v0(1+vc)
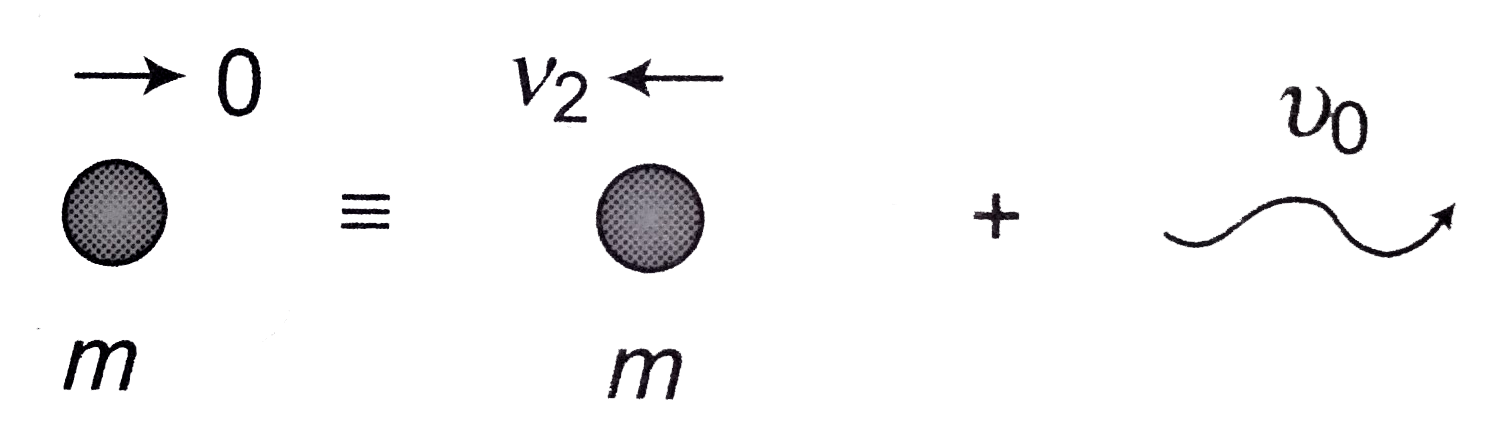
Topper's Solved these Questions
Similar Questions
Consider an excited hydrogen atom in state n moving with a velocity υ(υ<<c). It emits a photon in the direction of its motion and changes its state to a lower state m. Apply momentum and energy conservation principle to calculate the frequency v of the emitted radiation, compare this with the frequency v0 emitted if the atom were at rest.
View SolutionCalculate the energy and frequency of the radiation emitted when an electron jumps from n=3 to n=2 ina hydrogen atom.
View Solution
Knowledge Check
The frequency of 1st line Balmer series in H2 atom is v0. The frequency of line emitted by single ionised He atom is
A2v0B4v0Cv0/2Dv0/4what are the frequency and wavelength of a photon emitted during a transition from n = 5 state to the n =2 state in the hydrogen atom?
A434 nmB534 nmC400 nmD304 nmA hydrogen atom ia in excited state of principal quantum number n . It emits a photon of wavelength λ when it returnesto the ground state. The value of n is
A√λR(λR−1)B√λ(R−1)λRC√λRλR−1D√λ(R−1)
what are the frequency and wavelength of a photon emitted during a transition from n = 5 state to the n =2 state in the hydrogen atom?
View SolutionCalculate the energy and frequency of the radiation emitted when an electron jumps from n=3 to n=2 ina hydrogen atom.
View SolutionA hydrogen atom in the ground state is hit by a photon exctting electron to the thoird excerd state .The electron then drops to the second orbit. What is the frequency of radiation emitted and abserbed in the process ?
View SolutionState the relation between the frequency v of radiation emitted by a LED and the band gap energy Eg of the semiconductor used to fabricate it.
View SolutionIn hydrogen atom electron jumps from (n+1)th state to nth state the frequency of emitted photon is directly proportional to (n⟩1)
View Solution