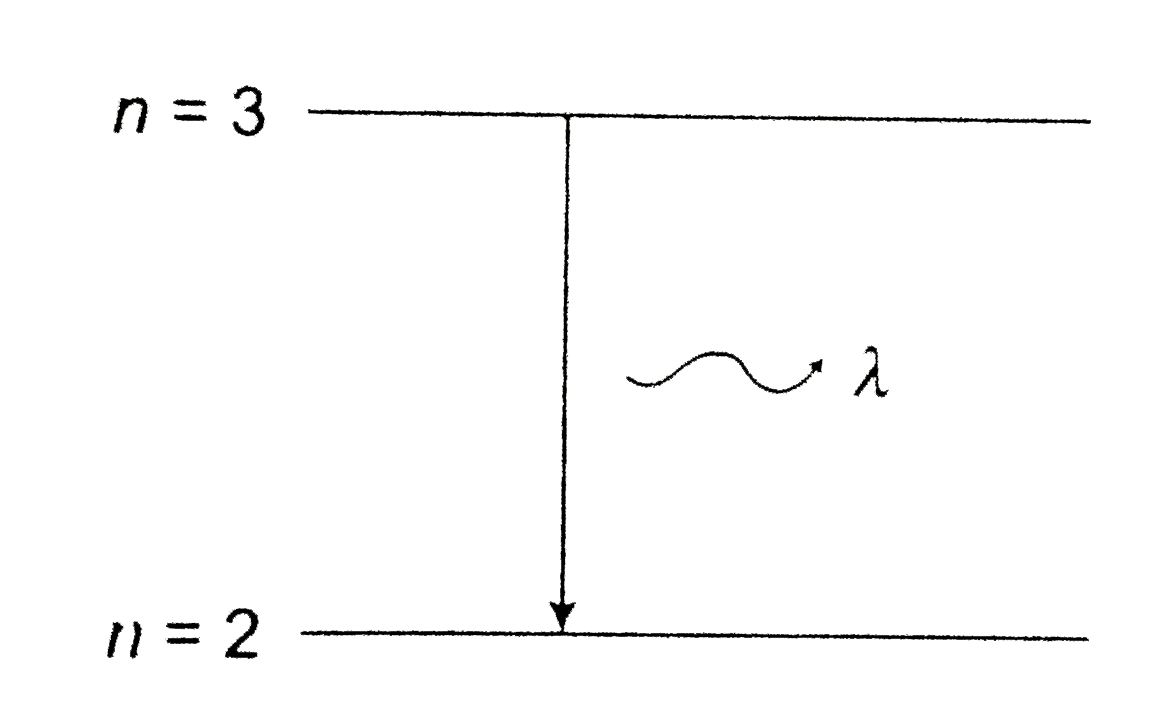
When a photon is emitted from an atom, the atom recoils. The kinetic energy of recoil and the energy of the photon come from the difference in energies between the states involved in the transition. Suppose, a hydrogen atom changes its state from n=3 to n=2. Calculate the fractional change in the wavelength of light emitted, due to the recoil.
ΔE=hcλ
λ=hcΔE (1)
ΔE=13.6(122−132)=1.9eV
Recoil of atom is considered
0=−mv+hλ'⇒v=hmλ'
ΔE=12mv2+hcλ'=12mh2m2λ'2+hcλ'
ΔE=h22mλ'2+hcλ'
λ'2ΔE−hcλ'−h22m=0
λ'=hc±√h2c2+4ΔEh22m2ΔE
=hc+√h2c2+2h2ΔEm2ΔE
=hc+hc√1+2ΔEmc22ΔE
λ'λ=1+(1+2ΔEmc2)1/22=1+1+ΔEmc22
=1+ΔE2mc2
λ'λ−1=ΔE2mc2=1.9×1.6×10−192×1.67×10−27x9×1016=10−9
Fractional change in wavelength =10−9.
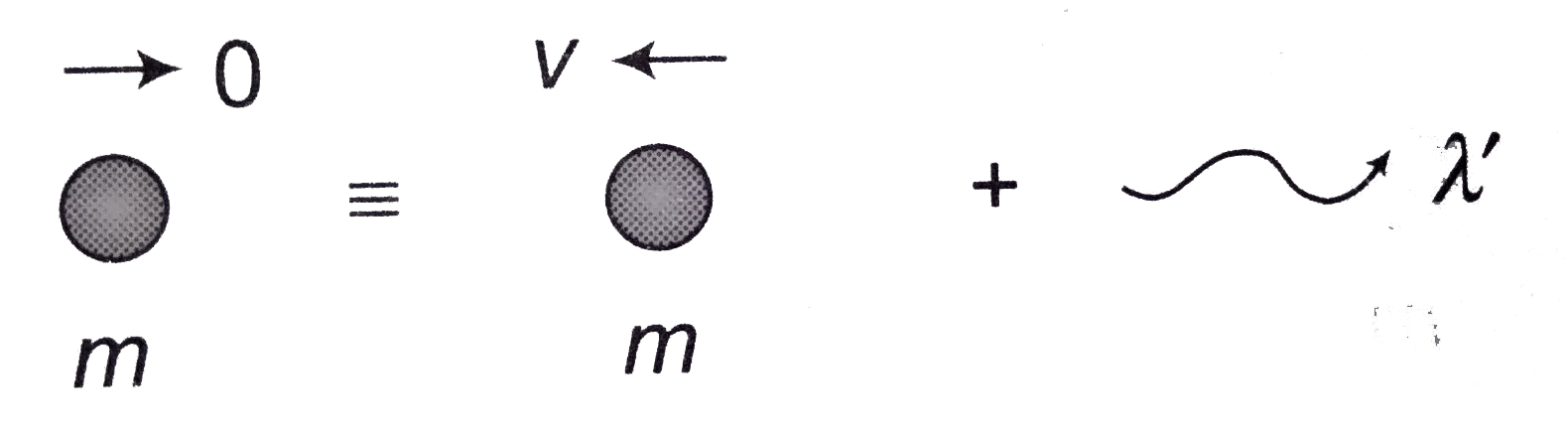
Topper's Solved these Questions
Similar Questions
When a photon is emitted from an atom , the atom recils The kinetic energy of recoils and the energy of the photon come from the difference in energy between the state involved in the transition suppose a hydrogen atom change its state from n=3→n=2 calculate the fractional change in the wavelength of light emitted , due to the recoil
View SolutionFrom the condition of the foregoing problem, find how much (in %) the energy of the emitted photon differs from the energy of the corresponding transition in a hydrogen atom.
View Solution
Knowledge Check
The energy change is greatest for a hydrogen atom when its state changes from
An=2→n=1Bn=3→n=2Cn=4→n=3Dn=5→n=4When a hydrogen atom emits a photon in going from n=5 to n=1, its recoil speed is almost
A10−4m/secB2×10−2m/secC4m/secD8×102m/secThe electron in a hydrogen atom at rest makes a transition from n=2 energy state to the n=1 ground state.
find the energy (eV) of the emitted photon.A5.8eVB8.3eVC10.2eVD12.7eV
When a hydrogen atom emits a photon in going from n=5 to n=1, its recoil speed is almost
View SolutionFrom the condition of the foregoing problems find how much (in pecent) the energy of the emitted photon differs from the energy of the corresponding transition in a hydrogen atom.
View SolutionElectron in a hydrogen atom makes a transition from higher energy states to n=2. Calculate the maximum possible wavelengths in this transition.
View SolutionIn a hydrogen atom , in transition of electron a photon of energy 2.55 eV is emitted , then the change in wavelenght of the eletron is
View SolutionThe wavelength of the photon emitted by a hydrogen atom when an electron makes a transition from n = 2 to n = 1 state is :
View Solution

