An electric dipole having charges +q and −q at a separation r. At distance d>>r along the axis of the dipole , the field is proportional to
qd2
qrd2
qd3
qrd3
The correct Answer is:4
To solve the problem of finding the electric field due to an electric dipole at a point along its axis at a distance much greater than the separation of the charges, we can follow these steps:
1. Understanding the Electric Dipole:
An electric dipole consists of two equal and opposite charges, +q and -q, separated by a distance r. The dipole moment p is defined as:
p=q⋅d
where d is the separation between the charges.
2. Positioning the Dipole:
Place the dipole along the x-axis with the positive charge +q at x=−r2 and the negative charge -q at x=r2. The point P where we want to find the electric field is located at a distance d from the center of the dipole (which is at the origin).
3. Calculating the Electric Field:
The electric field E at point P due to the positive charge +q is given by:
E1=k⋅q(d−r2)2
and the electric field due to the negative charge -q is:
E2=k⋅q(d+r2)2
4. Net Electric Field:
Since the electric fields due to the two charges are in opposite directions, the net electric field E at point P is:
E=E1−E2=k⋅q(d−r2)2−k⋅q(d+r2)2
5. Simplifying the Expression:
Factor out k⋅q:
E=k⋅q(1(d−r2)2−1(d+r2)2)
To combine the fractions, find a common denominator:
E=k⋅q⋅(d+r2)2−(d−r2)2(d−r2)2(d+r2)2
6. Using the Difference of Squares:
The numerator simplifies using the difference of squares:
(a2−b2)=(a−b)(a+b)
where a=d+r2 and b=d−r2:
E=k⋅q⋅(r)(r)(d−r2)2(d+r2)2
7. Considering d≫r:
When d is much greater than r, we can approximate:
(d−r2)2≈d2and(d+r2)2≈d2
Thus, the electric field simplifies to:
E≈2kqr2d3
8. Final Result:
The electric field at a distance d along the axis of the dipole is proportional to:
E∝pd3
where p=q⋅r is the dipole moment.
An electric dipole consists of two equal and opposite charges, +q and -q, separated by a distance r. The dipole moment p is defined as:
p=q⋅d
where d is the separation between the charges.
Place the dipole along the x-axis with the positive charge +q at x=−r2 and the negative charge -q at x=r2. The point P where we want to find the electric field is located at a distance d from the center of the dipole (which is at the origin).
The electric field E at point P due to the positive charge +q is given by:
E1=k⋅q(d−r2)2
and the electric field due to the negative charge -q is:
E2=k⋅q(d+r2)2
Since the electric fields due to the two charges are in opposite directions, the net electric field E at point P is:
E=E1−E2=k⋅q(d−r2)2−k⋅q(d+r2)2
Factor out k⋅q:
E=k⋅q(1(d−r2)2−1(d+r2)2)
To combine the fractions, find a common denominator:
E=k⋅q⋅(d+r2)2−(d−r2)2(d−r2)2(d+r2)2
The numerator simplifies using the difference of squares:
(a2−b2)=(a−b)(a+b)
where a=d+r2 and b=d−r2:
E=k⋅q⋅(r)(r)(d−r2)2(d+r2)2
When d is much greater than r, we can approximate:
(d−r2)2≈d2and(d+r2)2≈d2
Thus, the electric field simplifies to:
E≈2kqr2d3
The electric field at a distance d along the axis of the dipole is proportional to:
E∝pd3
where p=q⋅r is the dipole moment.
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDS Book:AAKASH INSTITUTEChapter:ELECTRIC CHARGES AND FIELDS Exercise:SECTION-B(OBJECTIVE TYPE QUESTION( ONLY ONE ANSWER)
Explore 11 Videos
- ELECTRIC CHARGES AND FIELDS Book:AAKASH INSTITUTEChapter:ELECTRIC CHARGES AND FIELDS Exercise:SECTION-C ( OBJECECTIVE TYPE QUESTIONS)
Explore 1 Video
- ELECTRIC CHARGES AND FIELDS Book:AAKASH INSTITUTEChapter:ELECTRIC CHARGES AND FIELDS Exercise:TRY YOURSELF
Explore 33 Videos
- DUAL NATURE OF RADIATION AND MATTER Book:AAKASH INSTITUTEChapter:DUAL NATURE OF RADIATION AND MATTER Exercise:ASSIGNMENT (SECTION-D)
Explore 10 Videos
- ELECTROMAGNETIC INDUCTIONBook:AAKASH INSTITUTEChapter:ELECTROMAGNETIC INDUCTIONExercise:ASSIGNMENT(SECTION -D) Assertion-Reason type Question)
Explore 15 Videos
Similar Questions
The mid points of two small magnetic dipoles of length d in end-on positions, are separated by a distance x, (x>>d). The force between them is proportional to x–n where n is:
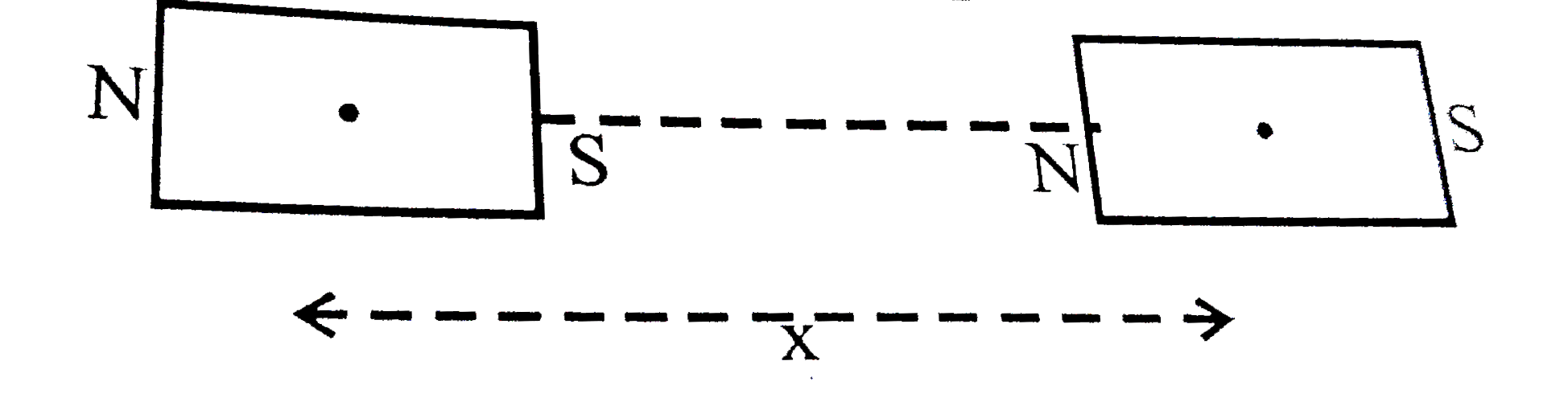
View SolutionTwo point charges q and −q are separated by the distance 2l. Find the flux of the electric field strength vector across a circle of radius R.

View Solution
Knowledge Check
A point Q lies on the perpendicular bisector of an electrical dipole of dipole moment p. If the distance of Q from the dipole is r (much larger than the size of the dipole), then electric field at Q is proportional to
Ap−1 and r−2Bp and r−2Cp2 and r−3Dp and r−3The electric field due to an extremely short dipole at distance r from it is proportional to :
A1rB1r2C1r3D1r4The electric field due to an extremely short dipole at distance r from it is proportional to :
A1rB1r2C1r3D1r4
Two point charges q and -q are separated by a distance 2a. Evaluate the flux of the electric field strength vector across a circle of radius R.

View SolutionTwo equal charges q of opposite sign separated by a distance 2a constitute an electric dipole of dipole moment p. If P is a point at a distance r from the centre of the dipole and the line joining the centre of the dipole to this point makes an angle θ with the axis of the dipole, then then potential at P is given by (f>>2a) where (p = 2 qa)
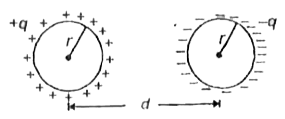
View SolutionTwo similar conducting balls having charges + q and - q are placed at a separation d from each other in air. The radius of each ball is r and the separation between their centres is d (d >> r ). Calculate the capacitance of the two ball system
View SolutionThe midpoint of two small magnetic dipoles d in end-on positions, are separated by a distance x,(x>>d). The force between them is proportional to x−n where n is:
View SolutionAn electric dipole is kept on the axis of a uniformly charged ring at distance d from the centre of the ring. The direction of the dipole moment is along the axis. The dipole moment is p, charge of the ring is Q & radius of the ring is R. The force on the dipole is
View Solution
