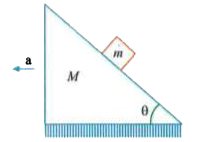
In the Fig. shown, mass 'm' is being pulled on the incline of a wedge of mass M. All the surface are smooth. Find the acceleration of the wedge.

Video Solution

Text Solution

Verified by Experts

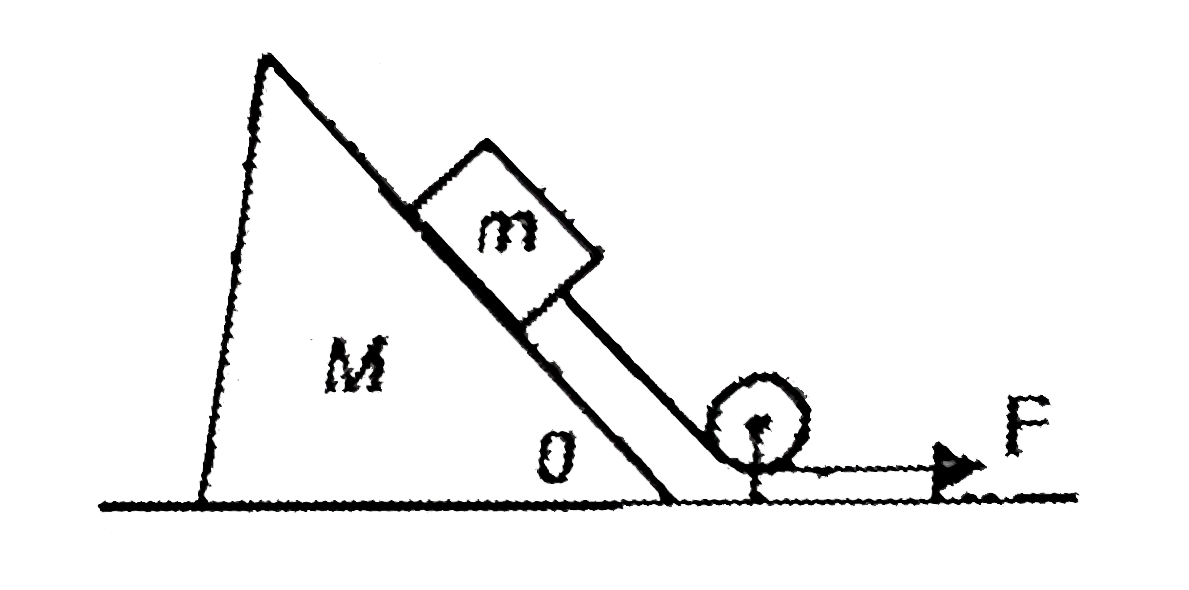
Free diagram of wedge .

Then by Newton 's 2nd law from above diagram
$N sin θ = M A$ …….(i)
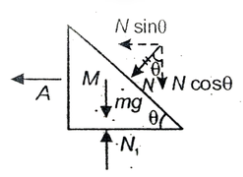
Free body diagram of block .

Now, by Newton's 2nd law from above diagram along the x- axis
$m A cos θ + m g sin θ = m a_{1}$ ....... (ii)
Along the y - axis , $N + m A sin θ = m g cos θ$ ......(iii)
From eq. (i) & (ii)
$\frac{M A}{sin θ} + m A sin θ = m g cos θ$
$A = \frac{m g sin θ cos θ}{M + m {sin}^{2} θ}$

Updated on:21/07/2023

|

Class 12 PHYSICS LAWS OF MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

In fig. mass $m$ is being pulled on the incline of a wedge of mass M. All the surfaces are smooth. Find the acceleration of the wedge.

A $a = \frac{F (1 - cos θ) m g 2 sin θ cos θ}{M + 2 m {sin}^{2} θ}$
B $a = \frac{F (1 + cos θ) + m g sin θ cos θ}{M + m {sin}^{2} θ}$
C $a = \frac{F (1 - cos θ) - m g sin θ cos θ}{M + m {sin}^{2} θ}$
D $a = \frac{F (1 + cos θ) - m g sin θ cos θ}{M - m {sin}^{2} θ}$
All surfaces are smooth. The acceleration of mass m relative to the wedge is

A $g sin θ$
B $g sin θ + a cos θ$
C $g sin θ - a cos θ$
D $a cos θ$
All surfaces are smooth The acceleration of mass m relative to the wedge is
.
A $g sin θ$
B $g sin θ + a cos θ$
C $g sin θ - a cos θ$
D $a cos θ$

AAKASH INSTITUTE-LAWS OF MOTION-Assignment (SECTION-D) (Assertion-Reason Type Questions)

Home
Ask Doubt
Profile