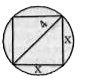
A square is inscribed in a circle of radius , a circle is inscribed in this square then a square in this circle and so on times. Find the limit of the sum of areas of all the squares as .
The correct Answer is:A
Step by step video, text & image solution for A square is inscribed in a circle of radius R, a circle is inscribed in this square then a square in this circle and so on n times. Find the limit of the sum of areas of all the squares as n to oo. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CONTINUITY AND DIFFERENTIABILITYBook:AAKASH INSTITUTEChapter:CONTINUITY AND DIFFERENTIABILITYExercise:Section - E
Explore 4 Videos
- CONTINUITY AND DIFFERENTIABILITYBook:AAKASH INSTITUTEChapter:CONTINUITY AND DIFFERENTIABILITYExercise:Section - F
Explore 3 Videos
- CONTINUITY AND DIFFERENTIABILITYBook:AAKASH INSTITUTEChapter:CONTINUITY AND DIFFERENTIABILITYExercise:Section - C ( More than one options are correct )
Explore 5 Videos
- CONIC SECTIONSBook:AAKASH INSTITUTEChapter:CONIC SECTIONSExercise:SECTION - J ( Aakash Challengers Questions )
Explore 14 Videos
- DETERMINANTS Book:AAKASH INSTITUTEChapter:DETERMINANTS Exercise:SECTION - J
Explore 12 Videos
Similar Questions
Knowledge Check
A square is inscribed in circle of radius R, a circle is inscribed in the square, a new square in the circle and so on for n times.
Sum of the areas of all circles isA4πR2(1−(12)n)B2πR2(1−(12)n)C3πR2(1−(13)n)DπR2(1−(12)n)If a square is inscribed in a circle of radius 7 cm, then find the area of the square (in cm2).
A49B98C196D392The area of the square inscribed in a circle of radius 8 cm is
A256 sq. cmB250 sq. cmC128sq. CmD125 sq. cm
In a circle of radius R a square is inscribed, then a circle is inscribed in the square, a new square in the circle and so on for n times. If the ratio of the limit of the sum of areas of all the circles to the limit of the sum of areas of all the squares as n→∞ is k, then find the value of 4kπ.
View SolutionA square ABCD is inscribed in a circle of radius r. Find the area of the square.
View SolutionThe area of a square inscribed in a circle of radius 8 cm is:
View Solutionone circle is inscribbed in a square with area "9pi" then area of square?
View SolutionIf a square is inscribed in a circle of radius 7 cm, then find the area of the square (in cm2).
View Solution