Given A = {1, 2). List all the relations on A.
To find all the relations on the set A = {1, 2}, we can follow these steps:
Step 1: Understand the concept of relations
A relation on a set A is a subset of the Cartesian product A × A. The Cartesian product A × A consists of all possible ordered pairs (a, b) where a and b are elements of A.
Step 2: Determine the elements of A × A
Given A = {1, 2}, we can find A × A:
- A × A = {(1, 1), (1, 2), (2, 1), (2, 2)}
Step 3: List all possible subsets of A × A
The number of subsets of a set with n elements is 2^n. Since A × A has 4 elements, the number of subsets (relations) is 2^4 = 16.
Step 4: Enumerate all subsets
We can list all subsets of A × A:
1. ∅ (the empty relation)
2. {(1, 1)}
3. {(1, 2)}
4. {(2, 1)}
5. {(2, 2)}
6. {(1, 1), (1, 2)}
7. {(1, 1), (2, 1)}
8. {(1, 1), (2, 2)}
9. {(1, 2), (2, 1)}
10. {(1, 2), (2, 2)}
11. {(2, 1), (2, 2)}
12. {(1, 1), (1, 2), (2, 1)}
13. {(1, 1), (1, 2), (2, 2)}
14. {(1, 1), (2, 1), (2, 2)}
15. {(1, 2), (2, 1), (2, 2)}
16. {(1, 1), (1, 2), (2, 1), (2, 2)} (the full relation)
Final Answer
The relations on A = {1, 2} are:
1. ∅
2. {(1, 1)}
3. {(1, 2)}
4. {(2, 1)}
5. {(2, 2)}
6. {(1, 1), (1, 2)}
7. {(1, 1), (2, 1)}
8. {(1, 1), (2, 2)}
9. {(1, 2), (2, 1)}
10. {(1, 2), (2, 2)}
11. {(2, 1), (2, 2)}
12. {(1, 1), (1, 2), (2, 1)}
13. {(1, 1), (1, 2), (2, 2)}
14. {(1, 1), (2, 1), (2, 2)}
15. {(1, 2), (2, 1), (2, 2)}
16. {(1, 1), (1, 2), (2, 1), (2, 2)}
A relation on a set A is a subset of the Cartesian product A × A. The Cartesian product A × A consists of all possible ordered pairs (a, b) where a and b are elements of A.
Given A = {1, 2}, we can find A × A:
- A × A = {(1, 1), (1, 2), (2, 1), (2, 2)}
The number of subsets of a set with n elements is 2^n. Since A × A has 4 elements, the number of subsets (relations) is 2^4 = 16.
We can list all subsets of A × A:
1. ∅ (the empty relation)
2. {(1, 1)}
3. {(1, 2)}
4. {(2, 1)}
5. {(2, 2)}
6. {(1, 1), (1, 2)}
7. {(1, 1), (2, 1)}
8. {(1, 1), (2, 2)}
9. {(1, 2), (2, 1)}
10. {(1, 2), (2, 2)}
11. {(2, 1), (2, 2)}
12. {(1, 1), (1, 2), (2, 1)}
13. {(1, 1), (1, 2), (2, 2)}
14. {(1, 1), (2, 1), (2, 2)}
15. {(1, 2), (2, 1), (2, 2)}
16. {(1, 1), (1, 2), (2, 1), (2, 2)} (the full relation)
The relations on A = {1, 2} are:
1. ∅
2. {(1, 1)}
3. {(1, 2)}
4. {(2, 1)}
5. {(2, 2)}
6. {(1, 1), (1, 2)}
7. {(1, 1), (2, 1)}
8. {(1, 1), (2, 2)}
9. {(1, 2), (2, 1)}
10. {(1, 2), (2, 2)}
11. {(2, 1), (2, 2)}
12. {(1, 1), (1, 2), (2, 1)}
13. {(1, 1), (1, 2), (2, 2)}
14. {(1, 1), (2, 1), (2, 2)}
15. {(1, 2), (2, 1), (2, 2)}
16. {(1, 1), (1, 2), (2, 1), (2, 2)}
Topper's Solved these Questions
- RELATIONS AND FUNCTIONS BOOK - AAKASH INSTITUTECHAPTER - RELATIONS AND FUNCTIONS EXERCISE - Try Yourself
70 Videos
- RELATIONS AND FUNCTIONS BOOK - AAKASH INSTITUTECHAPTER - RELATIONS AND FUNCTIONS EXERCISE - Assignment (Section - A) Objective Type Questions (one option is correct)
102 Videos
- PROBABILITYBOOK - AAKASH INSTITUTECHAPTER - PROBABILITYEXERCISE - ASSIGNMENT SECTION-J (aakash challengers questions)
13 Videos
- SEQUENCES AND SERIES BOOK - AAKASH INSTITUTECHAPTER - SEQUENCES AND SERIES EXERCISE - Assignment (SECTION - J) Aakash Challengers
12 Videos
Similar Questions
Knowledge Check
Match the relation for derivatives given in List II with the relation given in List I and then choose the correct code.
 AabcdqpsrBabcdspqrCabcdrqspDabcdqprs
AabcdqpsrBabcdspqrCabcdrqspDabcdqprs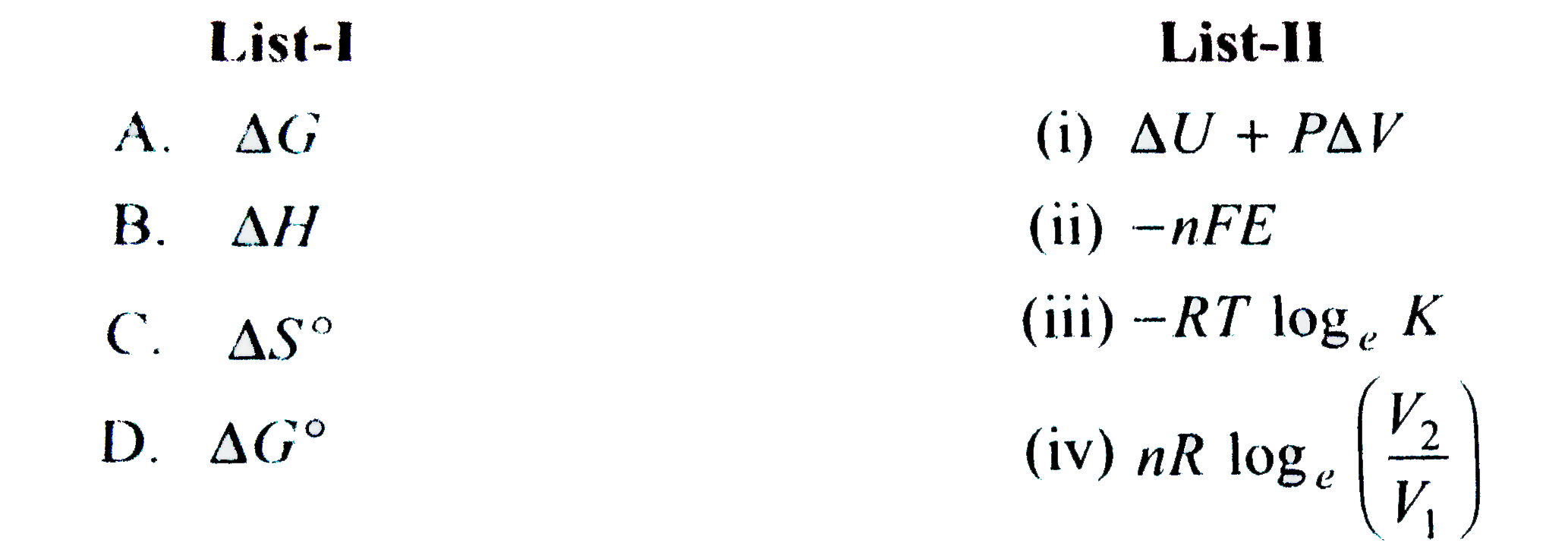 ltBrgt Match the physical changes in List-I with their relations given in List-II:AABCDiiiiviiiBABCDiiiiiiivCABCDiviiiiiiDABCDiiiiviii
ltBrgt Match the physical changes in List-I with their relations given in List-II:AABCDiiiiviiiBABCDiiiiiiivCABCDiviiiiiiDABCDiiiiviii
List all the prime factors of 72.
View SolutionList all the factors of 81.
View SolutionList all the factors of 27 and 52.
View SolutionGiven A={1,2,3}, then the relation R={(1,1),(2,2),(3,3)} is reflexive.
View SolutionMatch the statements given in the List-I with the equations given in List-II.
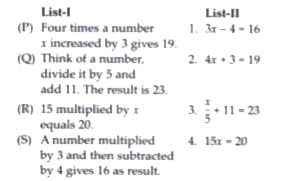
View SolutionMatch the quantities given in List-I to the respective ratios given in List-II.
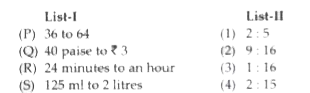
View Solution
