Question

Given a triangle ABC with $AB=2$ and $AC=1$. Internal bisector of $\angle BAC$ intersects BC at D. If AD = BD and $\Delta$ is the area of triangle ABC, then find the value of $12{\Delta }^2$.

Answer

9

Explanation

`AD=BD`

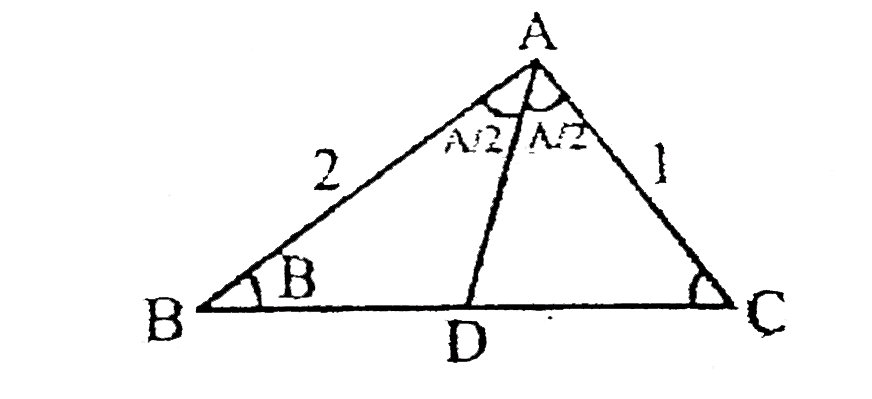
`:. (A)/(2) = B`
`A = 2B`
`C = pi - (A + B) = pi - 3B`
Using since Rule, in triangle `ABC`
`(sinB)/(1) = sin(pi-3B)/(2)`
`rArr 2sin B = sin 3B = (3 sin B - 4 sin^(3)B)`
`rArr 4 sin^(2)B = 1 rArr sin B = 1/2`
`:. B = 30^(@) , A = 60^(@) . C = 90^(@)`
`Delta = (1)/(2) xx 2 xx 1 xx sin A = sin A = (sqrt(3))/(2)`
`12Delta^(2) = 12 xx (3)/(4) = 9`.