In the triangle ABC, the internal bisector of angle A meets the side BC at D. If BD=7.5 cm and BC=9 cm. Then calculate the value of AB:AC.
2 :1
1 :2
5 :1
1 :3
The correct Answer is:A, C
To solve the problem, we will use the Angle Bisector Theorem, which states that the ratio of the lengths of the two segments created by the angle bisector on the opposite side is equal to the ratio of the lengths of the other two sides of the triangle.
1. Identify the Given Information:
- Let BD=7.5 cm
- Let BC=9 cm
2. Calculate DC:
- Since BC is the total length of side BC, we can find DC using the equation:
DC=BC−BD
- Substituting the values:
DC=9cm−7.5cm=1.5cm
3. Apply the Angle Bisector Theorem:
- According to the Angle Bisector Theorem:
ABAC=BDDC
- Substituting the values we found:
ABAC=7.51.5
4. Simplify the Ratio:
- To simplify 7.51.5:
7.5÷1.51.5÷1.5=51
5. Conclusion:
- Therefore, the ratio AB:AC is:
AB:AC=5:1
Final Answer:
The value of AB:AC is 5:1.
- Let BD=7.5 cm
- Let BC=9 cm
- Since BC is the total length of side BC, we can find DC using the equation:
DC=BC−BD
- Substituting the values:
DC=9cm−7.5cm=1.5cm
- According to the Angle Bisector Theorem:
ABAC=BDDC
- Substituting the values we found:
ABAC=7.51.5
- To simplify 7.51.5:
7.5÷1.51.5÷1.5=51
- Therefore, the ratio AB:AC is:
AB:AC=5:1
The value of AB:AC is 5:1.
Similar Questions
In △ABC,the bisector of ∠A intersect side BC at D. If AB=12cm, AC =15cm and BC=18cm , then the length of BD is:
△ABC में, ∠A का द्विभाजक BC को D पर प्रतिच्छेदित करता है| यदि AB = 12cm, AC = 15cm और BC= 18cm है, तो BD की लंबाई है:
View SolutionIn ΔABC with fixed length of BC , the internal bisector of angle C meets the side AB at D and meet the circumcircle at E. The maximum value of CD×DE is
View Solution
Knowledge Check
In △ABC, AD is the internal bisector of ∠S, meeting the side BC at D. If BD = 5cm, BC = 7.5 cm, then AB:AC is:
A3:5B4:5C1:2D2:1In ΔABC, AD is the internal bisector of ∠A, meeting the side BC at D. If BD=5cm,BC=7.5cm, then AB:ACis
A2:1B1:2C4:5D3:5In ΔABC, internal angle bisector of ∠A meet side BC in D. DE⊥AD meet AC in E and AB in F. then
AAE in H.M of b and cBAD=2bcb+ccos.A2CEF=4bcb+csin.A2DΔAEF is isosceles
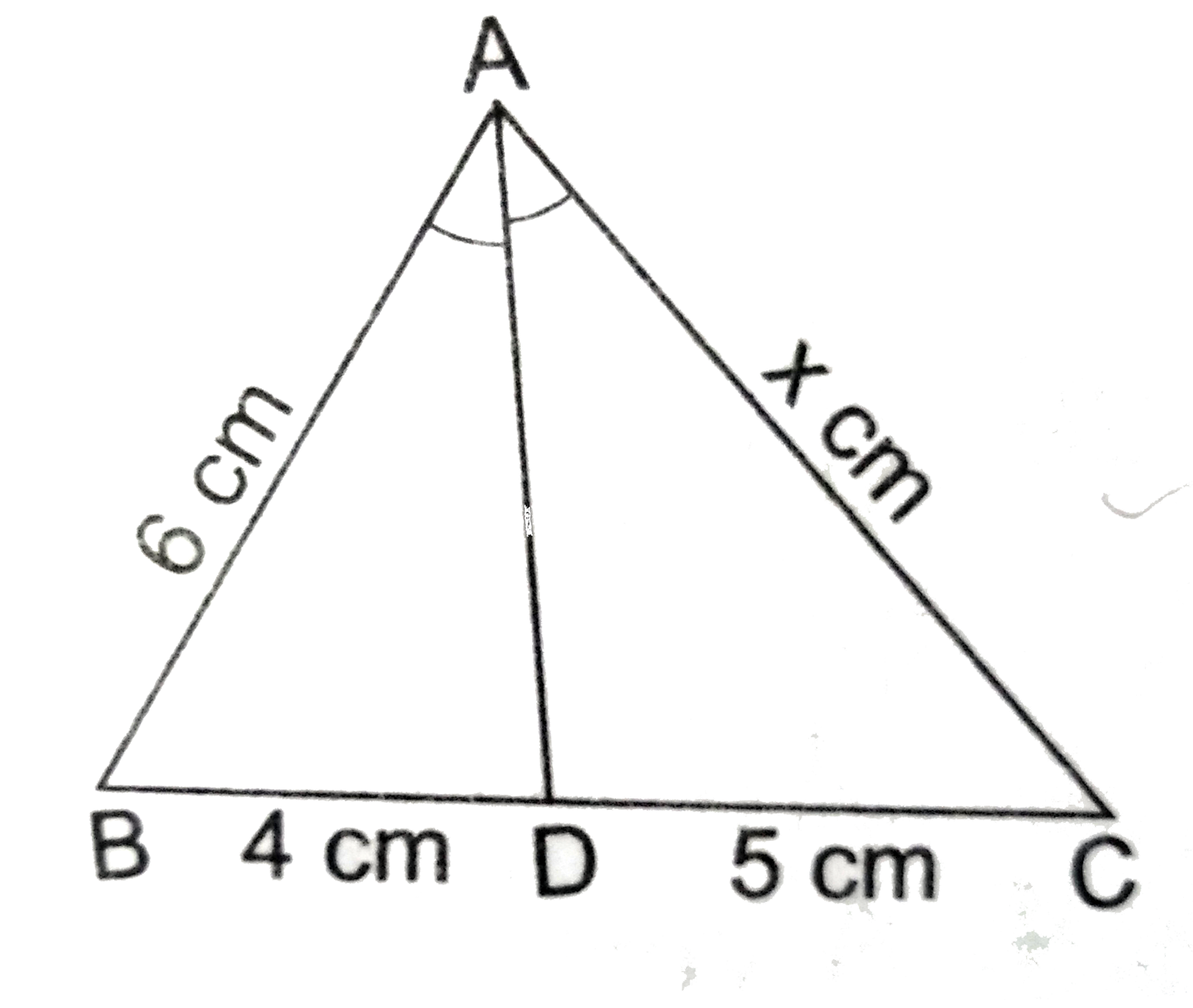
In a ΔABC it is given AD is internal bisector of ∠A . If BD=4cm,DC=5cmandAB=6cm, then AC =?
View SolutionIn △ABC, ∠A=90∘, AD is the bisector of ∠A meeting BC at D and DE⊥AC at E. If AB =10cm and AC = 15 cm, then the length of DE, in cm is:
△ABCमें ∠A=90∘, AD, ∠A का द्विभाजक है, जो BC से D पर मिलता है, और DE⊥AC से E पर मिलता है। यदि AB = 10 cm और AC= 15 cm है, तो DE की लंबाई(cm) है,
View SolutionIn a △ABC,AD is the angle bisector of ∠CAB and a median to BC. If AC=15 cm, find AB.
View SolutionIn a triangle ABC, angle bisector of ∠BAC cut the side BC at D and meet the circumcircle of ΔABC at E , then find AB .AC+DE. AE.
View SolutionIn ΔABC,AD is the inernal besector of ∠A. If BD = 5cm , BC=7.5 cm , then AB:AC=
View Solution
