Consider a plygon of sides 'n' which satisflies the equation 3..np4=.n−1p5
Number of quadrilaterals that can be made using the vertices of the polygon of sides 'n' if exactly two adjacent side of the quadrilateral are common to the sides of polygon is
A
50
B
60
C
70
D
.10C3−70
Video Solution
Text Solution
The correct Answer is:A, D
3.n!(n−4)!=(n−1)!(n−6)!,3n=(n−4)(n−5)
⇒3n=n2−9n+20⇒n2−12n+20=0
n=10,n=2 , not possible
so n=10
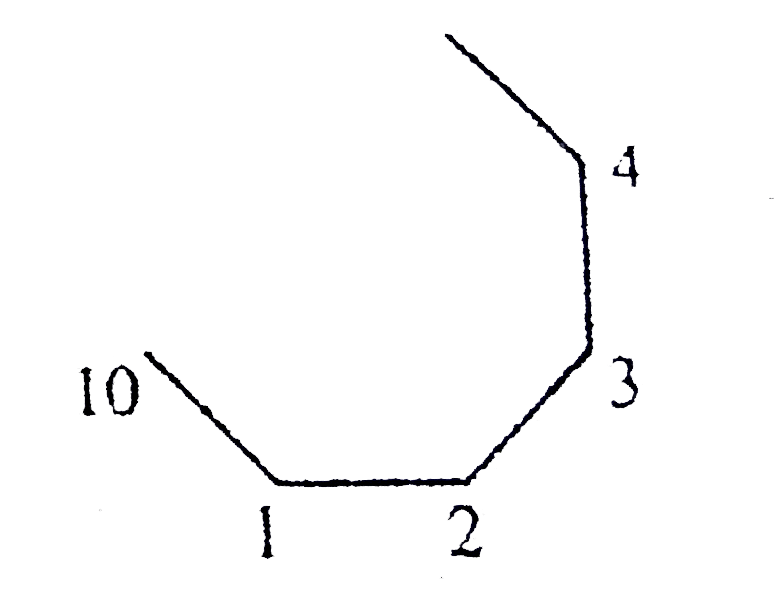
n=10
Consecutive two sides can be formed by (1,2,3) point 4,10 can't be selected but one point out of ramain 5 point can be.
selected in .5C1 ways
So total quadritaterals =10x5C1=50
|
Topper's Solved these Questions
- TEST PAPERSBook:RESONANCEChapter:TEST PAPERSExercise:Math
Explore 105 Videos
- TEST PAPERSBook:RESONANCEChapter:TEST PAPERSExercise:MATHEMATICS
Explore 263 Videos
- TEST PAPERSBook:RESONANCEChapter:TEST PAPERSExercise:PART - I MATHEMATICS SEC - 2
Explore 1 Video
- TEST PAPERBook:RESONANCEChapter:TEST PAPERExercise:CHEMISTRY
Explore 37 Videos
- TEST SERIESBook:RESONANCEChapter:TEST SERIESExercise:MATHEMATICS
Explore 131 Videos
Similar Questions
Knowledge Check
Consider a polygon of sides 'n' which satisfies the equation 3⋅.nP4=.n−1P5.
Q. Number of quadrilaterals that can be made using the vertices of the polygon of sides 'n' if exactly two adjacent sides of the quadrilateral are common to the sides of the n-gon isA50B60C70D80Consider a polygon of sides 'n' which satisfies the equation 3⋅.nP4=.n−1P5.
Q. Number of quadrilaterals thatn can be formed using the vertices of a polygon of sides 'n' if exactly 1 side of the quadrilateral in common with side of the n-gon, isA96B100C150D156Consider a plygon of sides 'n' which satisflies the equation 3..np4=.n−1p5
Rajdhani express travelling from Delhi to Mumbai has n station enroute. Number of ways in which a train can be stopped at 3 stationsAIf no two of the stopping are consecutive, is 56BIf no two of the stopping are consecutive, is 35CIf all the three stopping stations are consecutive, is 18DIf all the three stopping stations are consecutive, is 17
Number of quadrilaterals which can be constructed by joining the vertices of a convex polygon of 20 sides if none of the side of the polygon is also the side of the quadrilateral is
View SolutionFind the number of diagonals by joining the vertices of a polygon of n sides.
View SolutionThe number of different quadrilaterals that can be formed by using the vertices of a regular decagon, such that quadrilaterals has no side common with the given decagon, is
View SolutionFind the numbers of diagonals in the polygon of n sides.
View Solutionby using the vertices of a regular polygon of 12 sides,Pentagon's are formed.then no of Pentagons having no side common with the given polygon
View Solution

