Let f(x)=x2−5x+6,g(x)=f(|x|),h(x)=|g(x)|
The set of value of μ such that equation h(x)=μ has exactly 8 real and distinct roots, contains.
A
0
B
18
C
116
D
14
Video Solution
Text Solution
The correct Answer is:B, C
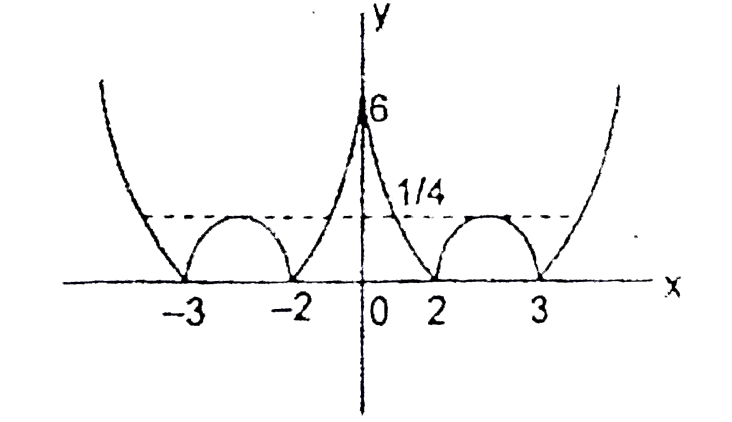
h(x)=|f(|x|)|
∴x∈(0,14)
|
Topper's Solved these Questions
- TEST PAPERSBook:RESONANCEChapter:TEST PAPERSExercise:Math
Explore 105 Videos
- TEST PAPERSBook:RESONANCEChapter:TEST PAPERSExercise:MATHEMATICS
Explore 263 Videos
- TEST PAPERSBook:RESONANCEChapter:TEST PAPERSExercise:PART - I MATHEMATICS SEC - 2
Explore 1 Video
- TEST PAPERBook:RESONANCEChapter:TEST PAPERExercise:CHEMISTRY
Explore 37 Videos
- TEST SERIESBook:RESONANCEChapter:TEST SERIESExercise:MATHEMATICS
Explore 131 Videos
Similar Questions
Knowledge Check
Let f(x)=x2−5x+6,g(x)=f(|x|),h(x)=|g(x)|
The set of values of x such that equation g(x)+|g(x)|=0 is satisfied containsA−3B0C2D52Let f(x)=x2−3x+2
g(x)=f(|x|)
h(x)=|g(x)|
are three functions. The complete set of values of x, for which the equation h(x)+g(x)=0 is satisfied, isAx∈[1,2]Bx∈[−2,−1]∪[1,2]Cx∈[−2,−1]DNone of theseLet f(x)=ex,g(x)=sin−1xandh(x)=f(g(x)) then h'(x)/h(x) =
Aesin−1xB1/√1−x2Csin−1xD1/(1−x2)
Let f(x)=x|x|, g(x)=sinx and h(x)=gof(x). Then
View SolutionLet f(x)=x,g(x)=1/xandh(x)=f(x)g(x). Then, h(x)=1, if
View SolutionLet f(x)=ex−x and g(x)=x2−x,∀x∈R. Then the set of all x∈R where the function h(x)=(fog)(x) in increasing is :
View SolutionIf f(x)=x, g(x)=√x2 and h(x)=x2x, then the set of values for which the given functions f(x), g(x) and h(x) are identical is :
View SolutionLet f(x)=x2+2x−5 and g(x)=5x+30
If h(x) = 5f(x)- xg(x), then what is the derivative of h(x)?
View Solution

