An uniform sphere is at rest and in equilibrium with the help of two vertical strings of unequal length larger string has length '2l' and shorter has length '7l'5. Both strings and centre of sphere are in one plane.

Radius of sphere is l. If ratio of fundamental frequancy in longer wire to shorter wire is k then 5√5k is (both strings are of same material)
The correct Answer is:7
An uniform………….
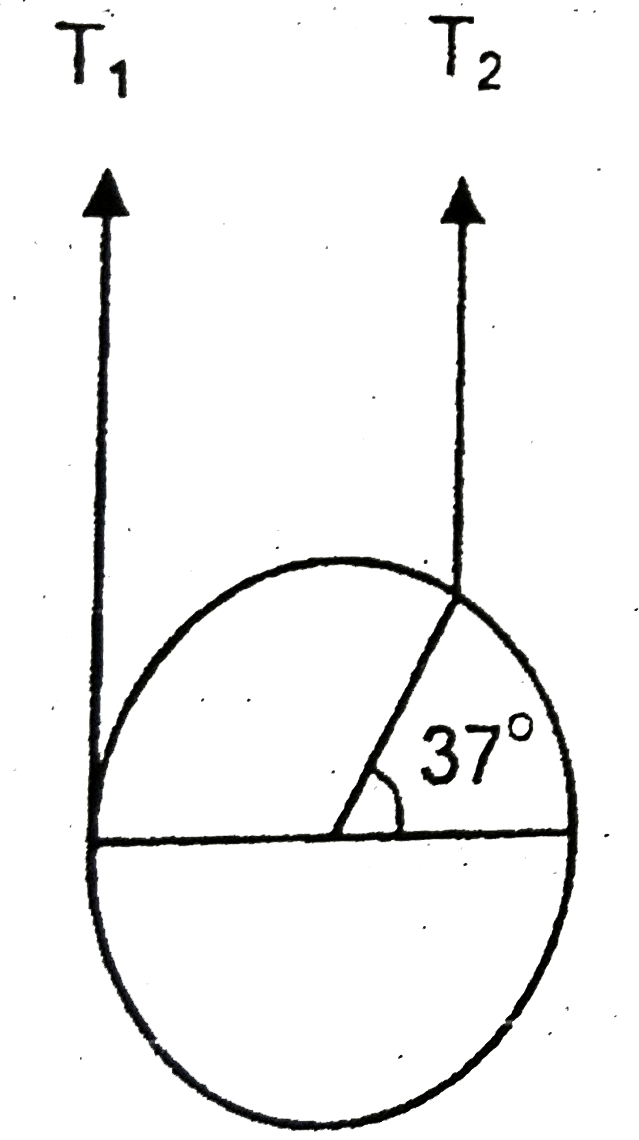
T1l=T2(4l5)
5T1=4T2
k=f1f2=√T1T2.l2l1
=√45.710=75√5
Similar Questions
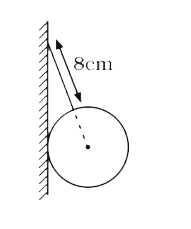
A uniform sphere of weight W and radius 5 cm is being held by string as shown in the figure. The tension in the string will be
View SolutionThe length , radius , tension and density of stringA are twice the same parameters of string B. Find the ratio of fundamental frequency of B to the fundamental frequency of A.
View Solution
Knowledge Check
A uniform rod is rested on a wall and its lower end is tied wall with the help of a horizontal string of negligble mass as shown. Length of rod is Land height of the wall is h. What will be tension in the string ?
 Amglsinθ2hcosθBmglcos2θ2hsinθCmglsinθcos2θ2hDmgl2hsinθcos2θ
Amglsinθ2hcosθBmglcos2θ2hsinθCmglsinθcos2θ2hDmgl2hsinθcos2θA string 1 has the length, twice the radius,two the tension and twice the density of another string The relation between the fundamental frequecy 1 and 2 is
Af1=2f2Bf1=4f2Cf2=4f1Df1=f2The length of a string is 5 meters . If 458 meters of string has cut , then find the length of the remaining string .
A38B78C58D18
In question 3 of the same exercise, the radius of the sphere is a. The length of the string is also a. Find tension in the string.
View SolutionAn object of mass m is suspended in equilibrium using a string of length l and a spring of constant K(<2mg/l) and unstretched length 1/2. Find the tension in the string. What happens if K>2mg/l?
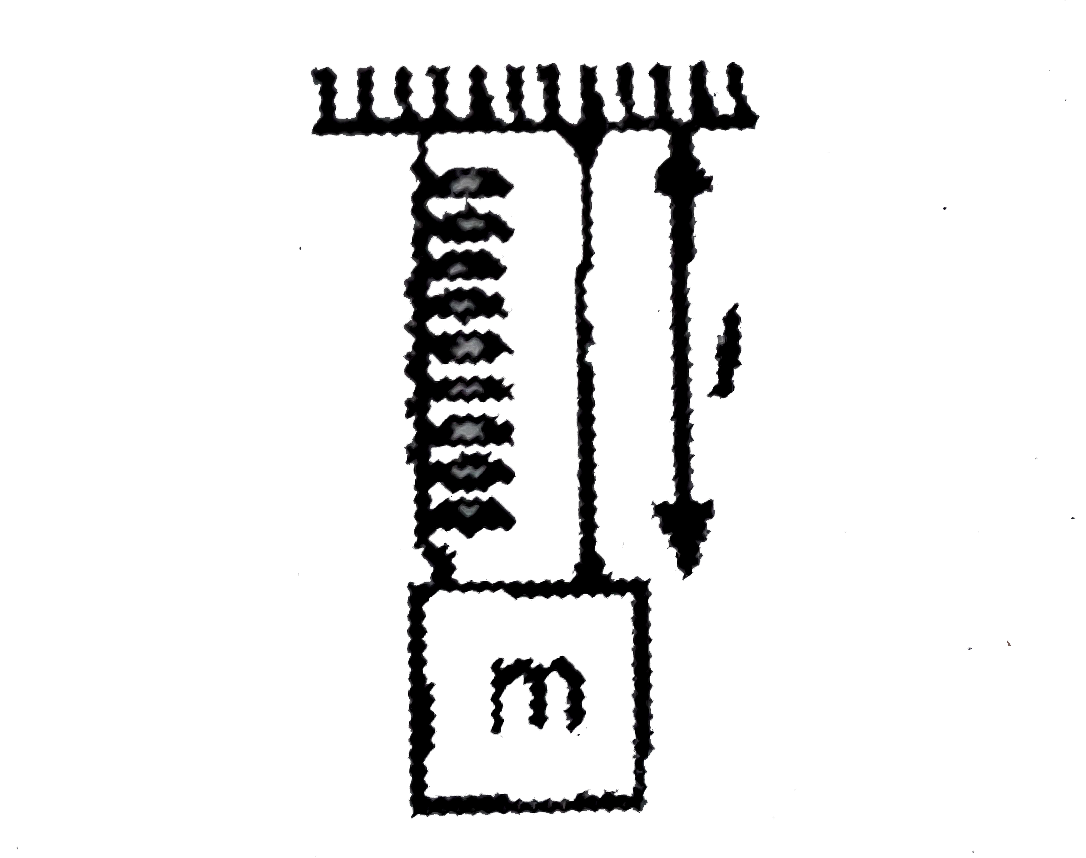
View SolutionTwo identical strings of same length are clamped at both the eads. Both strings vibrate 'with same fundamental frequency. If tension in one of the strings is increased by 21%, then 8 beats are produced per second. If fundamental frequency of strings in initial state is 10xHz.F∈dx.
View SolutionA stretched string fixed at both end has n nods, then the lengths of the string is
View SolutionThe linear mass density μ of the string is (where, mass of the string = m, length, of the string g = L)
View Solution