Find the distance travelled by a body having velocity v=1−t2 from t = 0 tol t = 2 sec .
3m
2m
1m
4m
The correct Answer is:B
Find the …………….

distance =∫20∣∣1−t2∣∣dt
distance =∫10(1−t2)dt+∫2−(1−t2)dt
distance =[t−t33]10−[t−t33]21=23−(−43)=2m
Similar Questions
The positions corrdinate of particle that is confined to move along a straight line is given by x=2t2−24t+6 where x is measured form a convenient origin and t is in second. Determine the distance travelled by the particle during the interval from t=1sec to t=4sec.
View SolutionFind the distance covered by a body in a free fall within the time interval t = a sec to t = b sec
View Solution
Knowledge Check
The position of a body moving along x-axis at time t is given by x=(t2−4t+6)m. The distance travelled by body in time interval t = 0 to t = 3 s is
A5 mB7 mC4 mD3 mA particle moves along x-axis and its acceleration at any time t is a = 2 sin (πt), where t is in seconds and a is in m/s2 . The initial velocity of particle (at time t = 0) is u = 0.
Q. Then the distance travelled (in meters) by the particle from time t = 0 to t = 1 s will be :A2πB1πC4π4Dnone of theseIf the distance s travelled by a body in time t is given by s=at+bt2 then the acceleration equals
A2at3+2bB2st2C2b−2at3Dst2
The distance travelled (in meters) by the particle from time t = 0 to t = t will be –
View SolutionFind displacement of a particle in 1-D if its velocity is v=(2t−5)m/s , from t=0 to t=4 sec.
View SolutionVelocity time equation of a particle moving in a straight line is v=2t−4 for t≤2s and v=4−2t for t>2.The distance travelled by the particle in the time interval from t=0 to t=4s is (Here t is in second and v in m/s)
View SolutionA particle moves along x-axis and its acceleration at any time t is a = 2 sin (πt), where t is in seconds and a is in m/s2 . The initial velocity of particle (at time t = 0) is u = 0.
Q. Then the distance travelled (in meters) by the particle from time t = 0 to t = t will be :
View SolutionIn the given v-t graph, the distance travelled by the body in 5 sec will be :
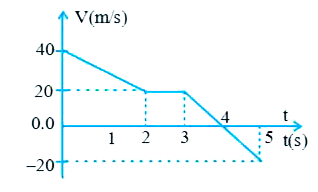
View Solution