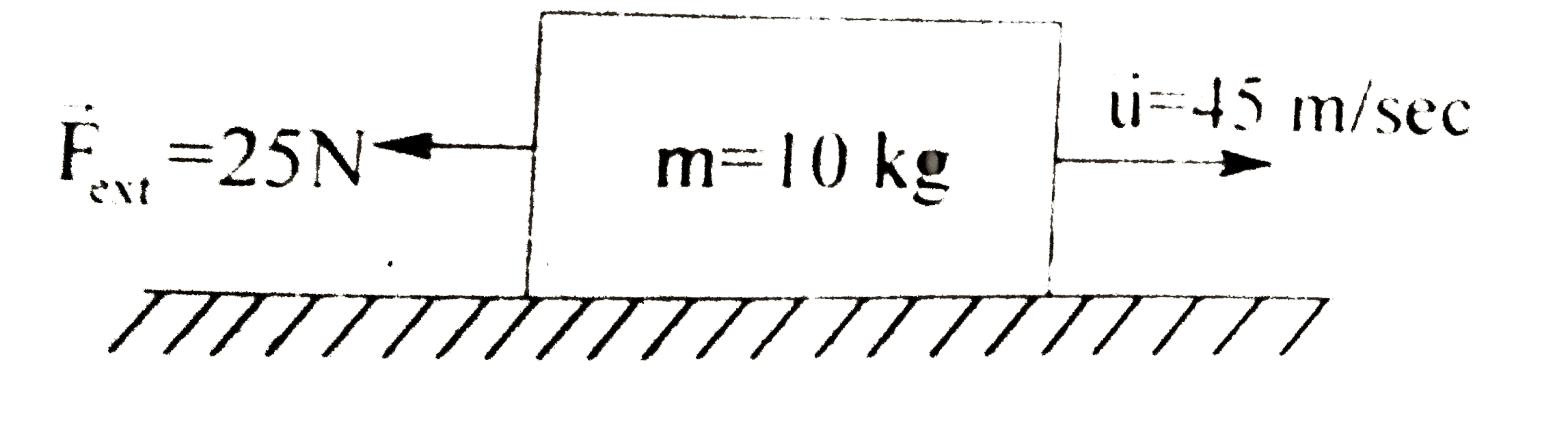
Initial velocity of the block →u=45ˆi while external force on it is →F=25(−ˆi) it coefficient of static and kinetic friction are 0.3 and 0.2 respectively then distance travelled by the block in 12 sec (g=10m/s2)
225 m
216 m
210 m
250 m
The correct Answer is:A
Net retardation a =Fext+μkmgm=4.5
if then stop at the t, then
V=u+at
0=45−4.5t⇒t=10sec
When block stops, Fext will try to bring the block back ward while frictional force will oppose its motion, since block is stationary therefore at this moment, frictional force will be static. Whose maximum value will be μsmg=30N. Since static frictional force is self adjusting therefore it will be 25 N and block will not move after t=10sec.
S=u22a=225m
Topper's Solved these Questions
- TEST PAPERSBOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS
747 Videos
- SIMPLE HARMONIC MOTIONBOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assignment Problems (Objective) (Level-II)
20 Videos
- WORK, ENERGY AND POWER BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - COMPREHENSIONS ( Comprehension-II)
5 Videos
Similar Questions
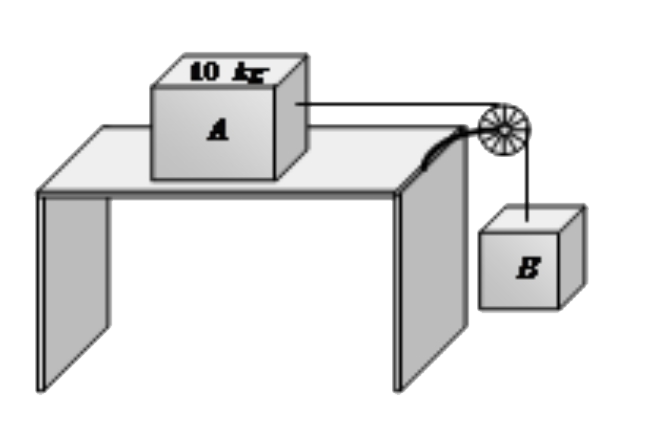
If the mass of the block A = 10 kg and the coefficient of static and kinetic friction is 0.2, then the mass of block B to start the motion is
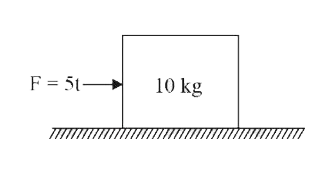
View SolutionA time varying force F = 5t is applied on a block kept on a rough horizontal surface. Mass of block is 10 kg, coefficient of static and kinetic friction between block and horizontal surface are 0.3 and 0.2 respectively. Take g = 10 m/s2 Find the time at which slipping starts between block and the surface beneath it.
View Solution
Knowledge Check
A block of mass 20kg is pushed with a horizontal force of 90N. It the coefficient of static and kinetic friction are 0.4 and 0.3, the frictional force acting on the block is (g=10ms−2) .
A90NB80NC60ND30NA block of mass 20 kg is pushed with a horizontal force of 90N. If the coefficient of static and kinetic friction are 0.4 and 0.3, the frictional force acting on the block is (g=10ms−2)
A90NB80NC60ND30NA 0.5kg block slides from the point A on a horizontal track with an initial speed 3m/s towards a weightless horizontal spring of length 1m and force constant 2N/m. The part AB of the track is frictionless and the part BC has the coefficient of static and kinetic friction as '0.22' and 0.20 respectively. If the distances AB and BD are 2m and 2.14m respectively, find total distance through which the block moves before it comes to rest completely. (g=10 m//s^(2) ).
A3.23 mB4.14 mC5.24 mD4.67 m
A 0.5kg block slides from the point A on a horizontal track with an initial speed 3m/s towards a weightless horizontal spring of length 1m and force constant 2N/m. The part AB of the track is frictionless and the part BC has the coefficient of static and kinetic friction as '0.22' and 0.20 respectively. If the distances AB and BD are 2m and 2.14m respectively, find total distance through which the block moves before it comes to rest completely. (g=10 m//s^(2) ).
View SolutionA slab of 40kg lying on a frictionales floor and a block of 10 kg rests on the slab as shown in the figure. The coefficients of static and kinetic friction between the slab and the block are 0.6 and 0.4 respectively. If a force of 100N is applied on the block, then the acceleration the slab will be (g=10m/s2)
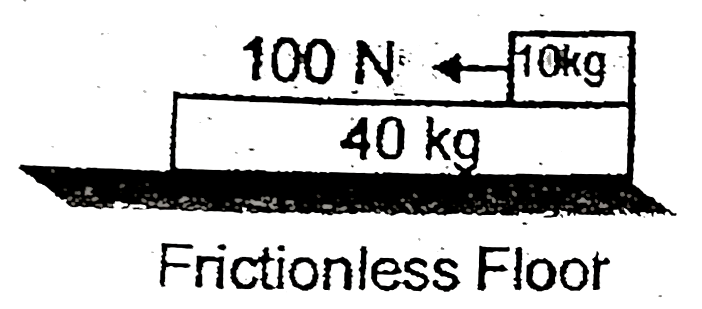
View SolutionA force of 750 N is applied to a block of mass 102 kg to prevent it from sliding on a plane with an inclination angle 30∘ with the horizontal. If the coefficients of static friction and kinetic friction between the block and the plane are 0.4 and 0.3 respectively, then the frictional force acting on the block is
View SolutionA block of mass 5kg is lying on a rough horizontal surface. The coefficient of static and kinetic friction are 0.3 and 0.1 and 10m/s−2. If a horizontal force of 50N is applied on the block, the frictional force is
View SolutionA block of mass 5kg is lying on a rough horizontal surface. The coefficient of static and Kinetic friction are 0.3and0.1 and g=10m/s−2 If a horizontal force of 50N is applied on the block, the frictional force is
View Solution
