
Equivalent thermal conductivity of figure given below will be given that length of eachh cylinder is l and area of cylinder having thermal conductivity K1 & K3 is A while middle cylinder is having K2.
52[1K1+12K2+1K3]
1(1K1+12K2+1K3)
25[1K112K2+1K3]
none of these
The correct Answer is:A
lK1A+l2K2A+lK3A=lKA+l2KA+lKA
52K=(1K1+12K2+1K3)
Keq=52(1K1+12K2+1K3)
Topper's Solved these Questions
- TEST PAPERSBOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS
747 Videos
- SIMPLE HARMONIC MOTIONBOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assignment Problems (Objective) (Level-II)
20 Videos
- WORK, ENERGY AND POWER BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - COMPREHENSIONS ( Comprehension-II)
5 Videos
Similar Questions
Thermal conductivity of inner core of radius r is K and of the outer one of radius 2r is 2K. Find equivalent value of thermal conductivity between its two ends.
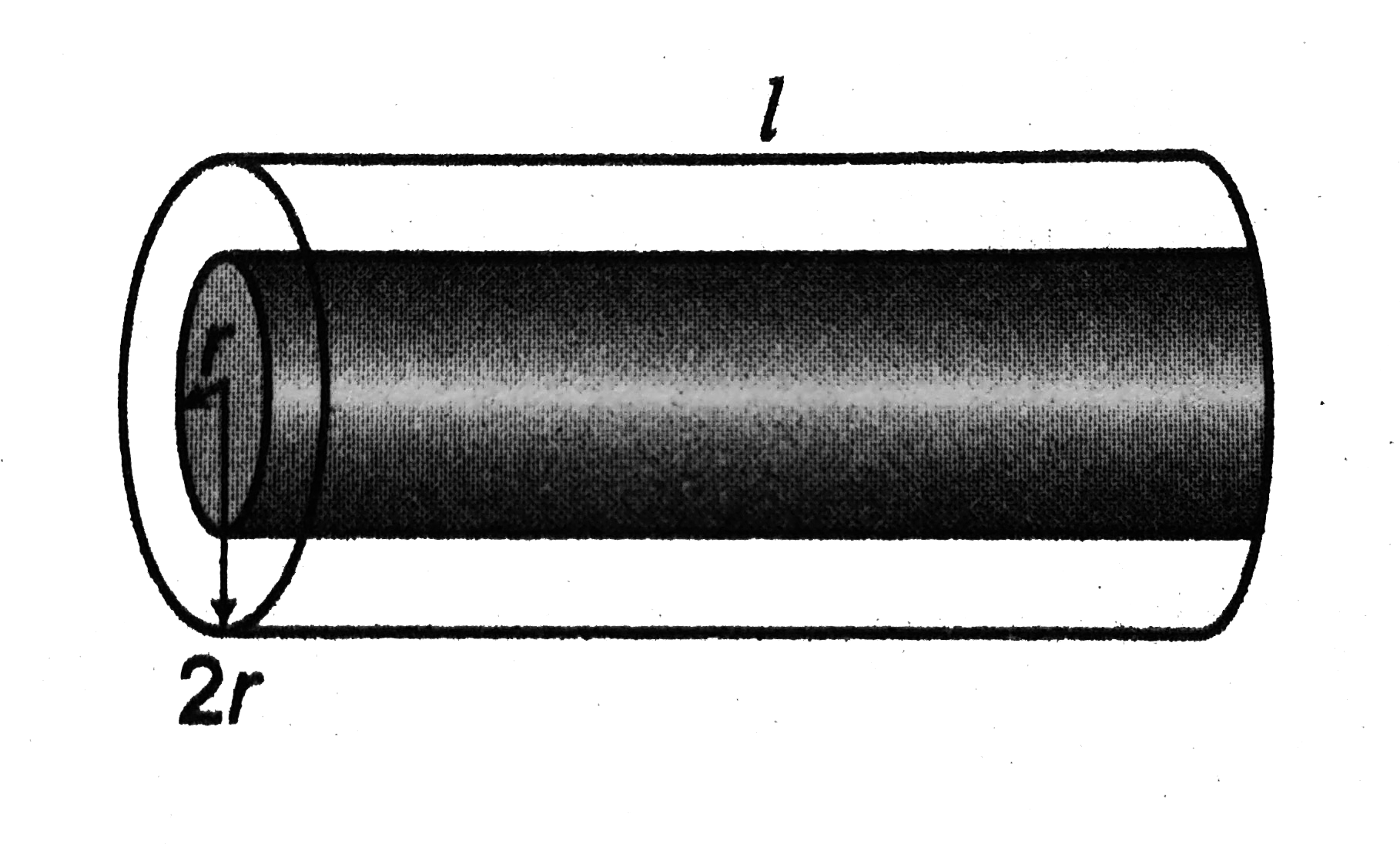
View SolutionCalculate thermal conductance for radial flow of an annular cylinder of length l and inner and outer radius r1 and r2. Assume that thermal conductivity of the material is K

View Solution
Knowledge Check
 Statement I: Two solid cylindrical rods of identical size and different thermal conductivity K1 and K2 are connected in series. Then the equivalent thermal conductivity of two rods system is less than that value of thermal conductivity of either rod.
Statement I: Two solid cylindrical rods of identical size and different thermal conductivity K1 and K2 are connected in series. Then the equivalent thermal conductivity of two rods system is less than that value of thermal conductivity of either rod.
Statement II: For two cylindrical rods of identical size and different thermal conductivity K1 and K2 connected in series, the equivalent thermal conductivity K is given by 2K=1K1+1K2AStatement I is true, Statement II is true and Statement II is the correct explanation for statement I.BStatement I is true, statement II is true and statement II NOT the correct explanation for Statement ICStatement I is true, Statement II is false.DStatement I is false, statement II is true.Three rods of same dimension are joined in series having thermal conductivity k1 , k2 and k3. The equivalent thermal conductivity is
Ak1k2k3/k2k3+k1k2+k1k3B3(k1k2k3)/k2k3+k1k2+k1k3Ck1+k2+k3D(k1+k2+k3)/ 3A cylinder A of a material of thermal conductivity K1 is surrounded by a cylindrical shell of inner radius equal to the cylinder. The shell is made of a material of thermal conductivity K2. The two ends of the combined system are maintained at two different temperature. if the effective thermal conductivity of the system is 4K1+5K29, find the rate of outer radius of the shell to the radius of the cylinder.
 A2.0B5/2C5/3D3/2
A2.0B5/2C5/3D3/2
A cylinder of radius R made of a material of thermal conductivity K1 is surrounded by cylindrical shell of inner radius R and outer radius 2R made of a material of thermal con-ductivity K2 The two ends of the combined system are maintained at two differnet tem-peratures There is no loss of heat across the cylindrical surface and system is in steady state What is the effective thermal conductivity of the system
 .
.
View SolutionCalculated thermal conductance for radial flow of a spherical sheel of inner and outer radius r1and r2. Assume that thermal conductivity of the material is K
View SolutionShow that the SI units of thermal conductivity are W/m−K.
View SolutionA cylinder of radius R is surrounded by a cylindrical shell of inner radius R and oputer radius 2R. The thermal conductivity of the material of the inner cylinder si k1 and that of the outer cylinder is K2 ,Assumming no loss of heat , the effective thermal conductivity of the system for heat flowing along the length of the cylionder is :
View SolutionA cylinder of radius R made of material of thermal conductivity K1 is surrounded by a cylindrical shell of inner radius R and outer radius 3R made of a material of thermal conductivity K2. The two ends of the combined system are maintained at two different temperatures. What is the effective thermal conductivity of the system ?
View Solution
