Show that if a body is projected vertically upward from the surface of the earth so as to reach a height nR above the surface
(i) the increase in its potential energy is (nn+1)mgR,
(ii) the velocity with which it must be projected is √2ngRn+1, where r is the radius of the earth and m the mass of body.
The correct Answer is:(i). [nn+1]mgR
(ii). √(nm+1)2gR
_E01_086_S01.png)
Ui=GMmR(1+n)⇒Ui=−GMmR
ΔUf−Ui=−GMmR[11+n−1]
by applying enegy conservation
12mv2=GMmR[1−11+n],v=√2GMR[1−11+n]
Topper's Solved these Questions
- GRAVITATIONBook:ALLENChapter:GRAVITATIONExercise:Exercise 4 B (Brain Storming Subjective Exercise)
Explore 20 Videos
- GRAVITATIONBook:ALLENChapter:GRAVITATIONExercise:Exercise 5 A (Previous Year Questions)
Explore 26 Videos
- GRAVITATIONBook:ALLENChapter:GRAVITATIONExercise:Exercise 3 (Miscellaneous Type Questions)
Explore 20 Videos
- GEOMETRICAL OPTICSBook:ALLENChapter:GEOMETRICAL OPTICSExercise:subjective
Explore 14 Videos
- KINEMATICS-2DBook:ALLENChapter:KINEMATICS-2DExercise:Exercise (O-2)
Explore 48 Videos
Similar Questions
Show that if a body be projected vertically upward from the surface of the earth so as to reach a height nR above the surface
(i) the increase in its potential energy is (nn+1)mgR,
(ii) the velocity with it must be projected is √2ngRn+1, where r is the radius of the earth and m the mass of body.
View SolutionA body is projected vertically upward from the surface of earth with a velocity sufficient to carry it to initially. Calculate the time taken by it to reach height h.
View Solution
Knowledge Check
A body is projected vertically upward from the surface of the earth, then the velocity-time graph is:-
A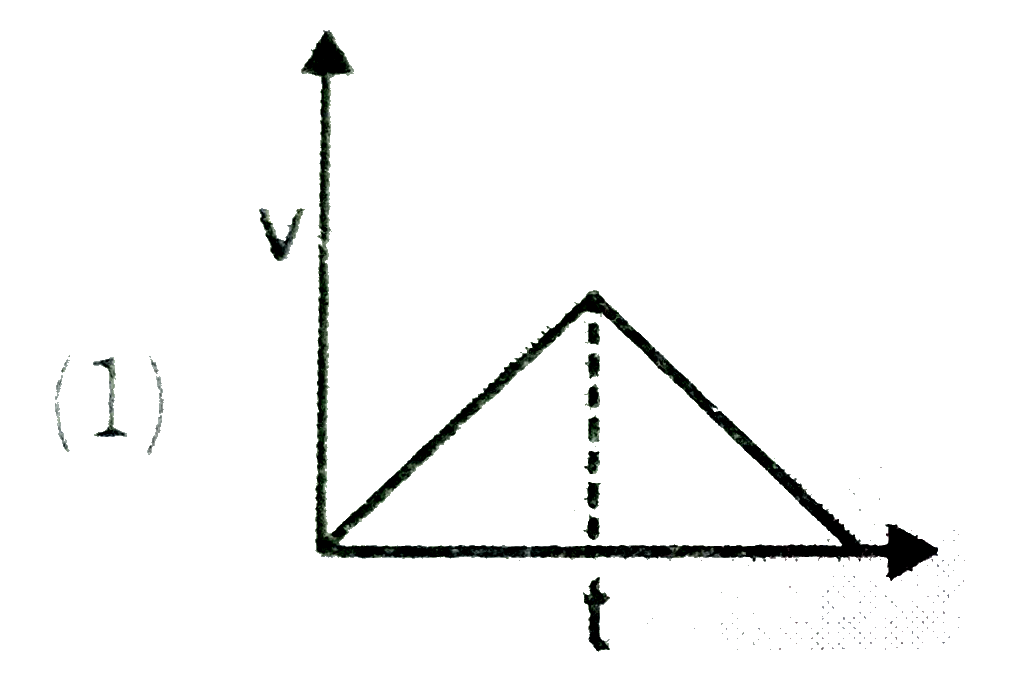 B
B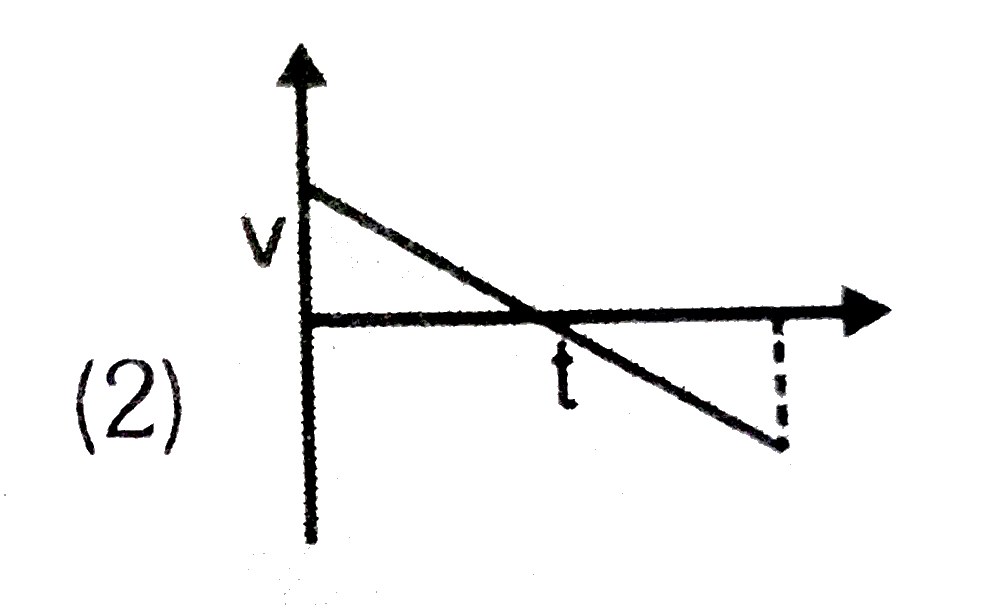 C
C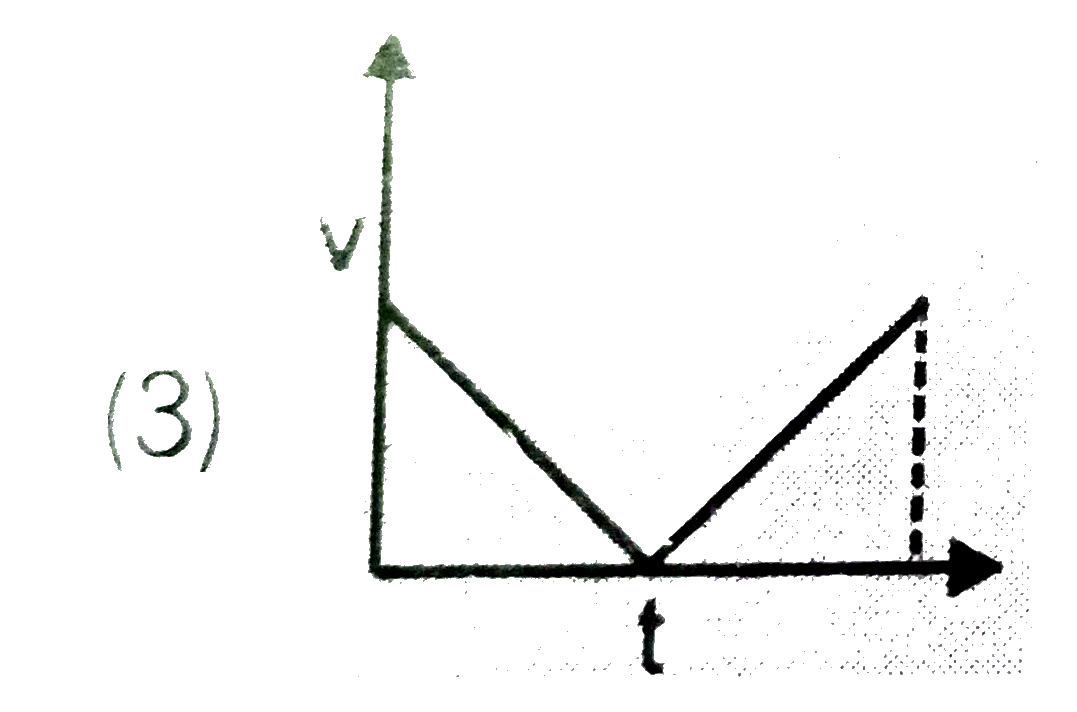 D
D
An object is taken to height 2R above the surface of earth , the increase in potential energy is [ R is radius of earth ]
AmgR2BmgR3C2mgR3D2mgRIf a body is to be projected vertically upwards from earth's surface to reach a height of 10R where R is the radius of earth. The velocity required to be si is
A√2411grB√2211grC√2011grD√1811gr
A body projected from the surface of the earth attains a height equal to the radius of the earth. The velocity with which the body was projected is
View SolutionA body of mass m is taken from earth surface to the height h equal to radius of earth, the increase in potential energy will be
View SolutionA body is projected vertically up from surface of the earth with a velocity half of escape velocity. The ratio of its maximum height of ascent and radius of earth is
View SolutionA body of mass m rises to a height h=R/5 from the surface of earth. If g is the acceleration due to gravity at the surface of earth, the increase in potential energy is (R = radius of earth)
View SolutionThe escape velocity of a body projected vertically upwards from the surface of the earth is v.If the body is projected in a direction making an angle θ with the vertical, the vetical, the escape velocity would be
View Solution