An equi-convex lens of $(μ = 3 / 2)$ and focal length 10 cm is held with its axis vertical and its lower surface immersed in water $(μ = 4 / 3)$ , the upper surface being in air. At what distance from the lens, will a vertical beam of parallel light incident of the lens be focused?

Video Solution

Text Solution

Verified by Experts

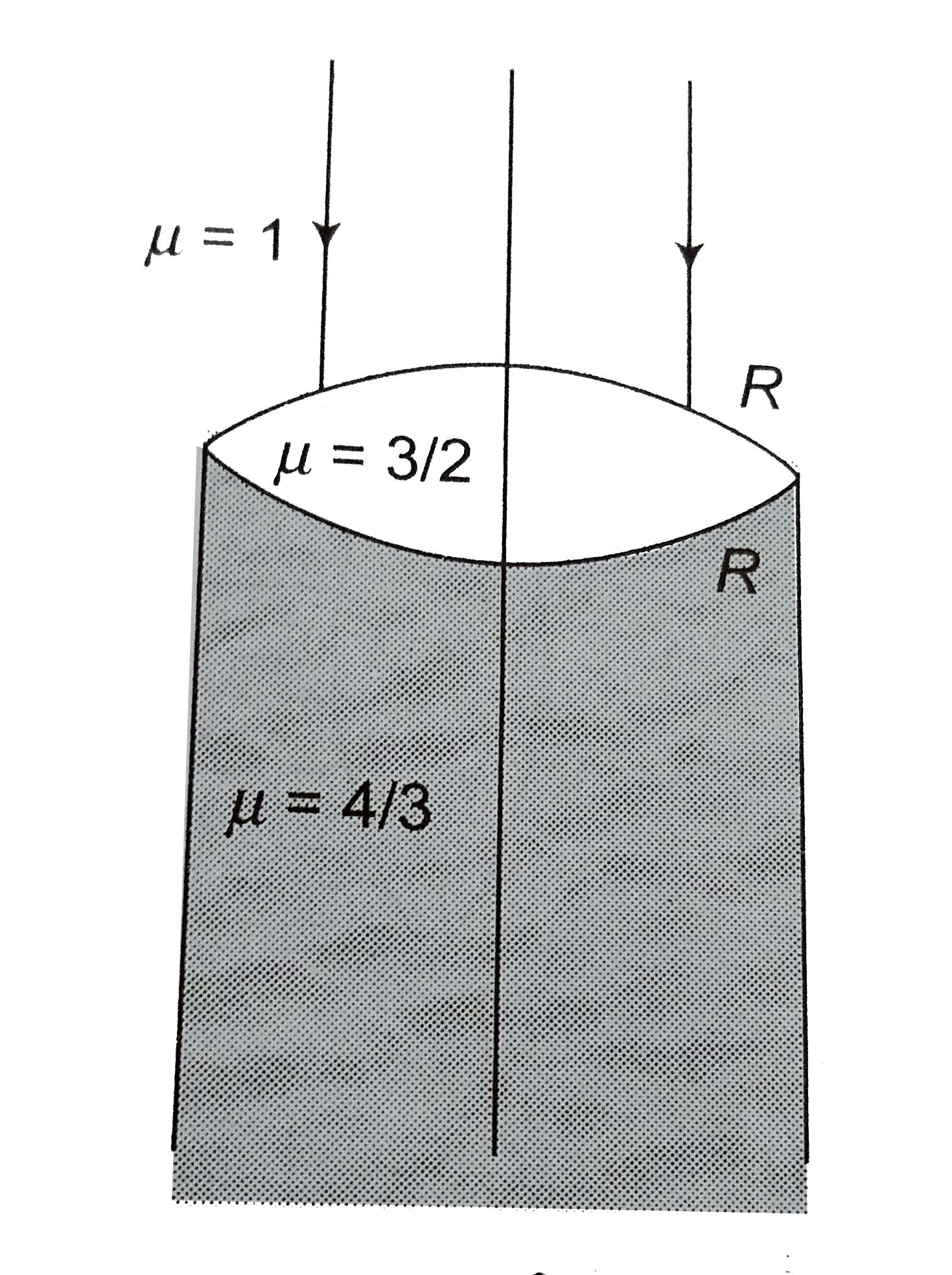
First determine radius of curvature of equi-convex lens
$\frac{1}{f} = (μ - 1) (\frac{1}{R_{1}} - \frac{1}{R_{2}})$
$\frac{1}{10} = (\frac{3}{2} - 1) (\frac{1}{R} - \frac{1}{- R}) = \frac{1}{R} \Rightarrow R = 10 c m$
Here incident rays are parallel to principal axis i.e., $u = \infty$ focal length is being asked
$μ_{1} = 1, μ_{2} = \frac{3}{2}, μ_{3} = \frac{4}{3}, R_{1} = 10 c m, R_{2} = - 10 c m$
$\frac{μ_{3}}{f} = \frac{μ_{2} - μ_{1}}{R_{1}} + \frac{μ_{3} - μ_{2}}{R_{2}}$
$\frac{\frac{4}{3}}{f} = \frac{\frac{3}{2} - 1}{10} + \frac{\frac{4}{3} - \frac{3}{2}}{- 10}$
$\frac{4}{3 f} = \frac{1}{20} + \frac{1}{60} = \frac{1}{15}$
$f = 20 c m$

Updated on:21/07/2023

A convex lens is of focal length 10 cm. What is its power?
A $+ 10 D$
B $+ 5 D$
C $- 10 D$
D $+ 1 D$
Focal length of a glass lens in air is 2.5 cm. Its focal length when immersed in water would be
A $2 \times 2.5 c m$
B $4 \times 2.5 c m$
C $6 \times 2.5 c m$
D $(\frac{2.5}{4}) c m$
A convex lens of glass $(n = \frac{3}{2})$ has a focal length 20 cm. The lens is immersed in water of refractive index $\frac{4}{3}$ . What is the change in the power of convex lens ?
A1.75 D
B3.75 D
C4.5 D
D5.75 D