A hollow sphere of glass of inner and outer radii R and 2R respectively has a small mark on its inner surface. This mark is observed from a point outside the sphere such that the centre of the sphere lies in between. Prove that the mark will appear nearer than it really it, by a distance (μ−1)(R)/(3μ−1)
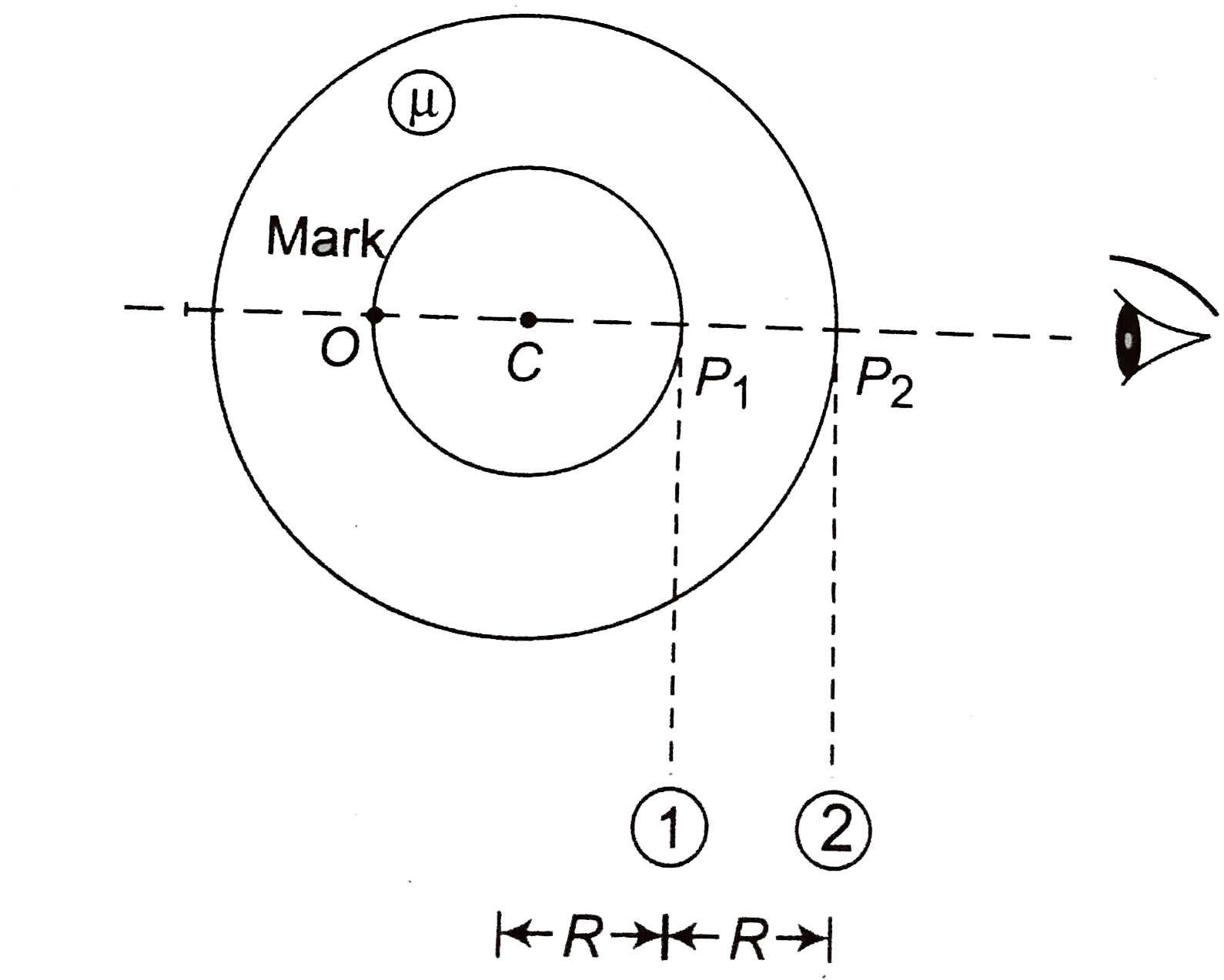
Refraction at 1:
μ1=1,μ=μ,u=−2R,R=−R,v=?
μv−1−2R=μ−1−R
μv=1−μR−12R=2−2μ−12R
v=2μR1−2μ=−2μR2μ−1
Refractiojn at 2:
μ1=μ,μ2=1,u=−(R+2μR2μ−1)=−(4μ−12μ−1)R.
1v−μ−(4μ−12μ−1)R=1−R−2R
1v=μ−12R−μ(2μ−1)(4μ−1)R
=(μ−1)(4μ−1)−2μ(2μ−1)2(4μ−1)R
=−3μ+12(4μ−1)R
v=−2(4μ−1)R(3μ−1)
P2O=3R,P2I2=2(4μ−1)R3μ−1
OI2=P2O−P2I2=3R−2(4π−1)R(3μ−1)=(μ01)R(3μ−1)
Topper's Solved these Questions
- REFRACTION AT SPHERICAL SURFACESBOOK - CP SINGHCHAPTER - REFRACTION AT SPHERICAL SURFACESEXERCISE - EXERCISES
105 Videos
- REFLECTION OF LIGHTBOOK - CP SINGHCHAPTER - REFLECTION OF LIGHTEXERCISE - EXERCISES
67 Videos
- REFRACTION OF LIGHT BY PLANE SURFACESBOOK - CP SINGHCHAPTER - REFRACTION OF LIGHT BY PLANE SURFACESEXERCISE - Exercises
110 Videos
Similar Questions
A hollow sphere made of a transparent material of refractive index 1.5 has a small mark on its surface as shown. The mark is observed from the farther side. Find the distance of the image of mark from the centre of the sphere.
View SolutionA hollow sphere of glass of R.I .n has small mark M on its interior surface which is observed by an observer O from a point outside the sphere, .C is centre of the sphere. The inner cavity (air) is concentric with the external surface and thickness of the glass is every where equal to the radius of the inner surface. Find the distance by which the mark will appear nearer than it really is in terms of n and R assuming paraxial rays.
_E01_156_Q01.png)
View Solution
Knowledge Check
A hollow conducting sphere of inner radius r and outer radius 2R is given charge Q as shown in figure, then the
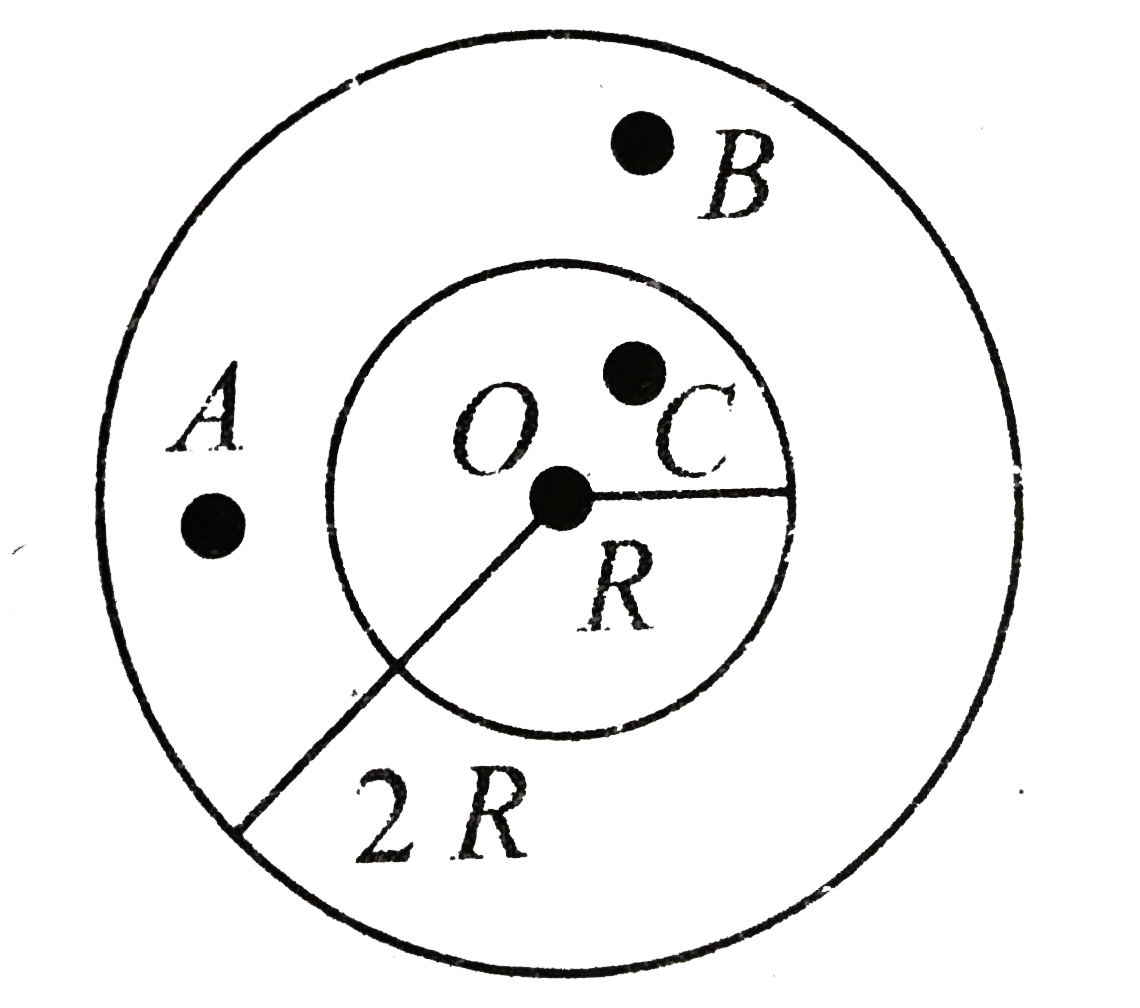Apotential at A and B is same.Bpotential at O and B is same.Cpotential at O and C is same.Dpotential at A,B,C and O is same.A metallic sphere having inner and outer radii a and b respectively has thermal conductivity
K=K0r(a≤r≤b)
Find the thermal resistance between inner surface and outer surface.A(b−a)4πK0B(b2−a2)4πKaabC4πK0(b−a)Dnone of theseThere is a sphere of radius R and refractive index μ. At what distance from the surface of sphere should an object be placed so that real image is formed at the same distance from the sphere ?
ARμ−1BRμCR2−μD2Rμ−1
A hollow metallic sphere has inner and outer radii, respectively as 5 cm and 10 cm if the mass of the sphere is 2.5 kg, find (a) density of the material, (b) relative density of the material of the sphere.
View SolutionA small filament is at the centre of a hollow glass sphere of inner and outer radii 8 cm and 9 cm respectively. The refractive index of glass is 1.50. Calculate the position of the image of the filament when viewed from outside the sphere.
View SolutionIn a conducting hollow sphere of inner and outer radii 5cm and 10cm respectively, a point charge 1 μC is placed at point A, thaUs 3cm from the centre C of the hollow sphere. An external uniform electric field of magnitude 20 N/C is also applied. Net electric force on the this. charge is 15N, away from the away from the centre of the sphere as shown in figure−1.455. Find magnitude of force exerted by the charge placed at point A on the sphere:
centre of the sphere as shown in figure. Find magnitude
View SolutionA hollow cylinder of specific resistance ρ, inner radius R, outer radius 2R and length 1 is as shown in figure. What is the net resistance between the inner and outer surfaces?
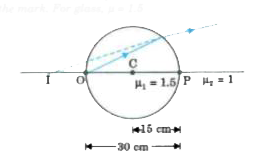
View SolutionA mark placed on the surface of glass sphere is viewed through glass from an oppositely directed position. If the diameter of the sphere is 30 cm, locate the image of the mark. For glass, μ=1.5
View Solution