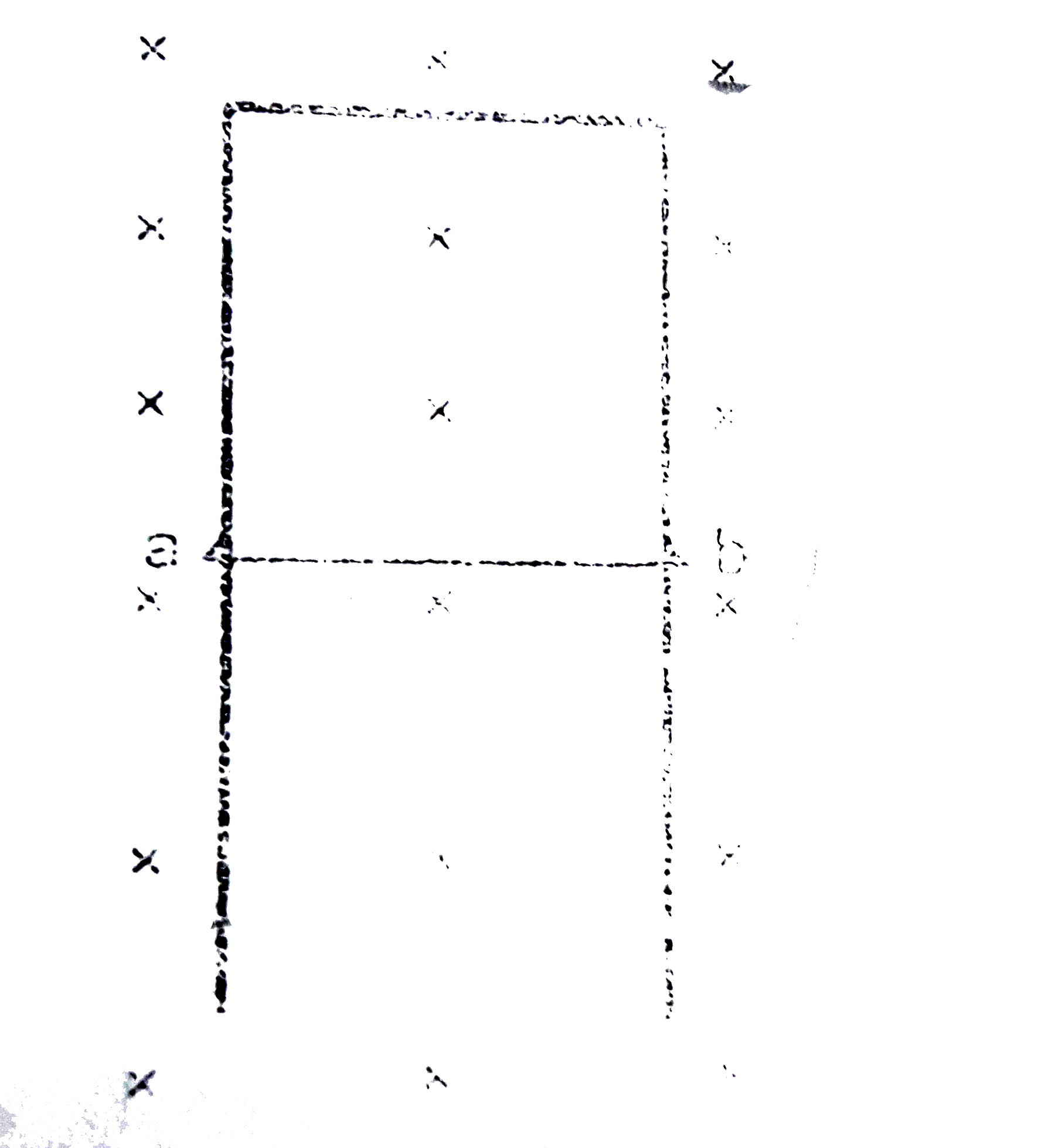
A conducting wire ab of length l, resistance r and mass m starts sliding at t = 0 down a smooth, vertical, thick pair of connected rails as shown in . A uniform magnetic field B exists in the space in a diraction perpendicular to the plane of the rails. (a) Write the induced emf in the loop at an instant t when the speed of the wire is v. (b) what would be the magnitude and direction of the induced current in the wire? (c) Find the downward acceleration of the wire at this instant. (d) After sufficient time, the wire starts moving with a constant velocity. Find this velocity v_m. (e) Find the velocity of the wire as a function of time. (f) Find the displacement of the wire as a functong of time. (g) Show that the rate of heat developed inte wire is equal to the rate at which the gravitational potential energy is decreased after steady state is reached.
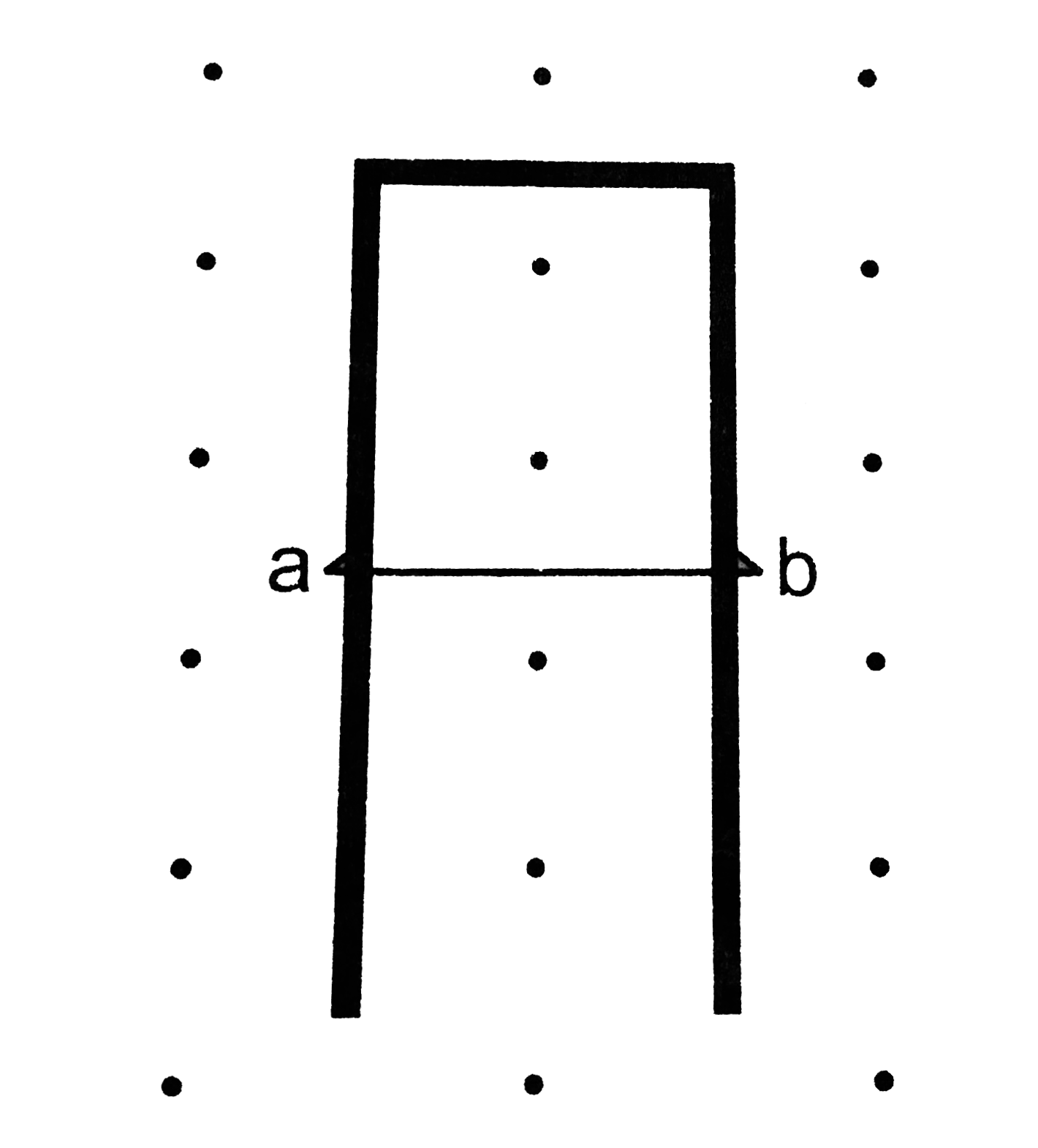
When velocity of rod is v
induced emf e=Bvl
(b) Induiced current I=eR=BvlR
Flux is increasing, induced current in the loop is clockwise.
(c) Magnetic force on the wire
Fm=BIL=B2vl2R , upward
mg−Fm=ma
a=g−Fmm=g−B2l2vmR
(d) When v=vm , a=0
g−B2l2vmmR=0⇒vm=mgRB2l2
(e) In steady state, the wire falls with constant velocity vm
Rate of heat developed P1=I2R=(B2v2ml2/R)=mgvm
Rate at which gravitational potenital enregy decreases
p2=ddt(mgh)=mg(dhdt)=mgvm
P1=P2


Topper's Solved these Questions
Similar Questions
A rod of mass m, length l and resistance R is sliding down on a smooth inclined parallel rails with a cinstant velocity v. If a uniform horizontal magnetic field B exists, then find thevalue of B.
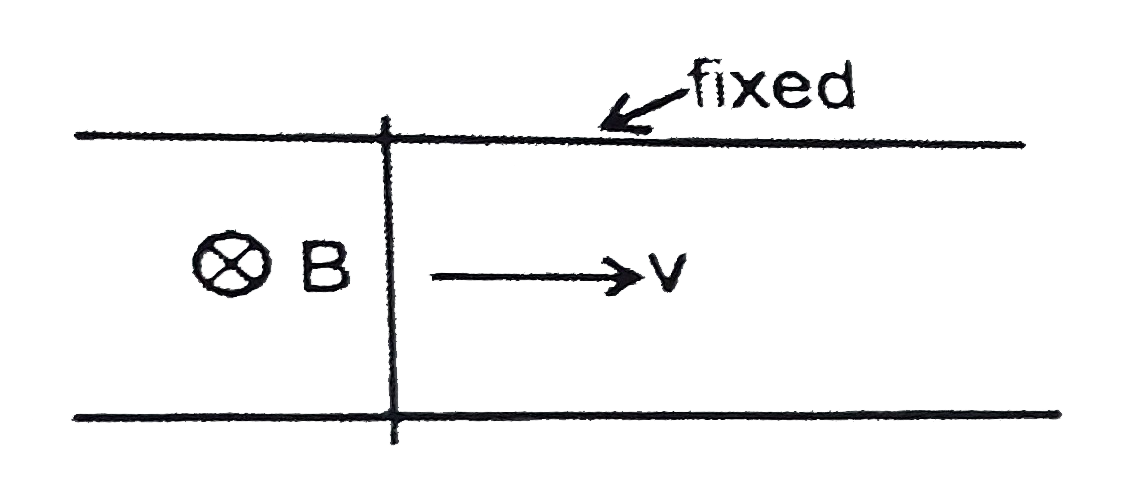
View SolutionFigure shows a wire of resistance R sliding on two parallel, conducting fixed thick rails placed at a separation l. A magnetic fild B exist in a direction perpendicular to the plane of the rails. The wire is moving with a constant velocity v. Find current through the wire
View Solution
Knowledge Check
A copper wire ab of length l, resistance r and mass m start sliding at t=0 down a smooth, vertical, thick pair of connected conducting rails as shown in figure. A uniform magnetic field B exists in the space in a direction perpendicular to the plane of the rails which options are correct .
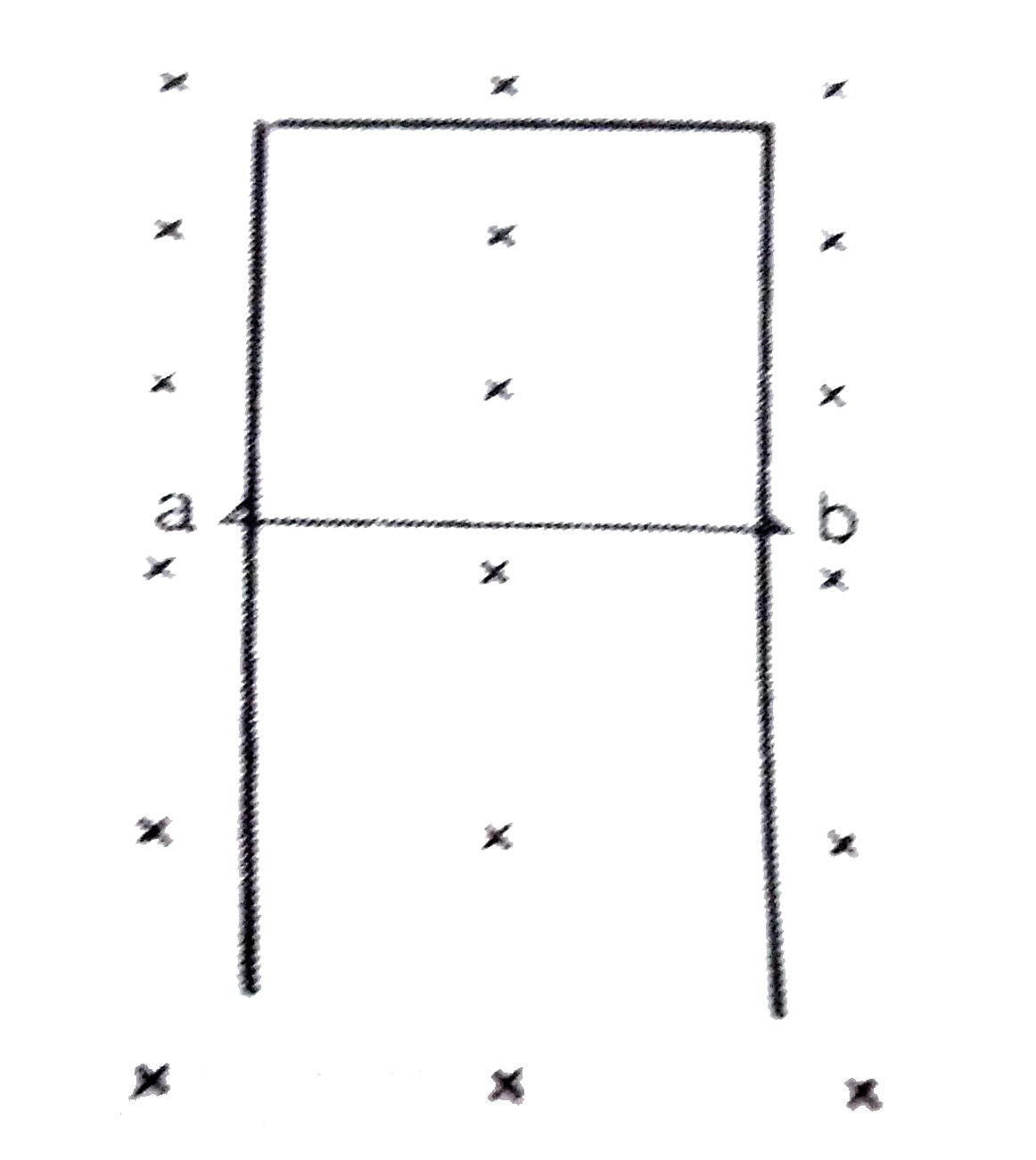 AThe magnitude and direction of the induced current in the wire when speed of the wire v is vBlr, a to bBThe downward acceleration of the wire at this instant g−B2l2mrvCThe velocity of the wire as a function of time vm(1−e−gt/vm),(wherevm=mgrB2l2)DThe displacement of the wire as a function of time vmt−v2mg(1−e−gt/vm),(wherevm=mgrB2l2)
AThe magnitude and direction of the induced current in the wire when speed of the wire v is vBlr, a to bBThe downward acceleration of the wire at this instant g−B2l2mrvCThe velocity of the wire as a function of time vm(1−e−gt/vm),(wherevm=mgrB2l2)DThe displacement of the wire as a function of time vmt−v2mg(1−e−gt/vm),(wherevm=mgrB2l2)A copper wire ab of length l, resistance r and mass m starts sliding at t=0 down a smooth, vertical, thick pair of connected condcuting rails as shown in figure.A uniform magnetic field B exists in the space in a direction perpendicular to the plane of the rails which options are correct.
 AThe magnitude and direction of the induced current in the wire when speed of the wire v is vBlr, a to bBThe downward acceleration of the wire at this instant g−B2l2mrv.CThe velocity of the wire as a function of time vm(1−e−gt/vm)(where vm=mgrB2l2)DThe displacement of the wire as a function of time vmt−v2mg(1−e−gt/vm)(where vm=mgrB2l2)
AThe magnitude and direction of the induced current in the wire when speed of the wire v is vBlr, a to bBThe downward acceleration of the wire at this instant g−B2l2mrv.CThe velocity of the wire as a function of time vm(1−e−gt/vm)(where vm=mgrB2l2)DThe displacement of the wire as a function of time vmt−v2mg(1−e−gt/vm)(where vm=mgrB2l2)A conducting wire ab of length l resistance r and mass m starts sliding down at t=0 on a smooth, vertical thick pair of connected rails as shown. The terminal speed of the wire is
 AmgRBlBmgrB2l2CmglB2r2DNone
AmgRBlBmgrB2l2CmglB2r2DNone
A conducting wire xy of lentgh l and mass m is sliding without friction on vertical conduction rails ab and cd as shown in figure. A uniform magnetic field B exists perpendicular to the plane of the rails, x moves with a constant velocity of

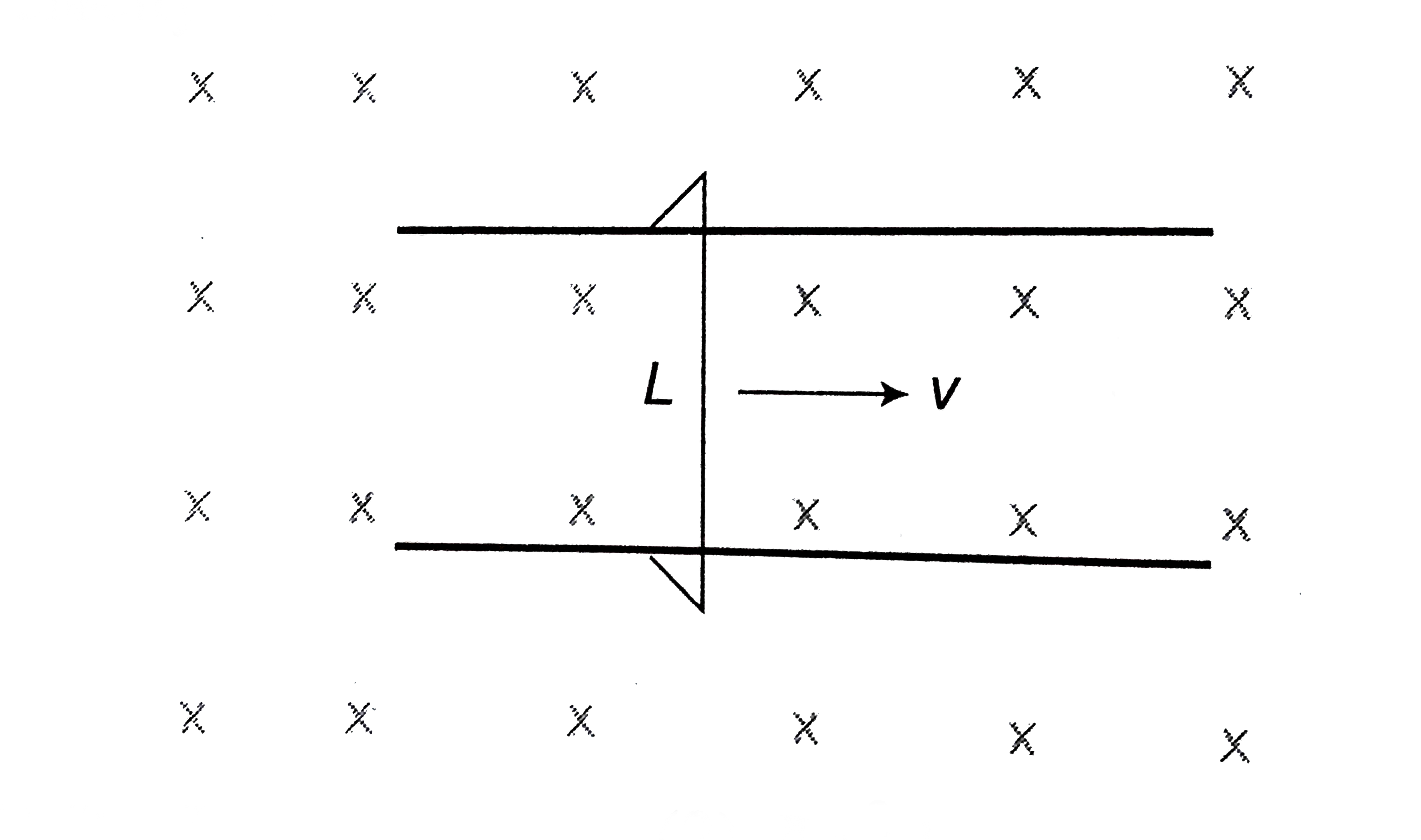
View SolutionFigure shows a wire sliding on two parallel, conducting rails placed at a separation L . A magnetic field B exists in a direction perpendicular to the plane of the rails. What force is necessary to keep the wire moving at a constant velocity V ?
View SolutionA conducting square loop is placed in a magnetic field B with its plane perpendicular to the field. Now the sides of the loop start shrinking at a constant rate α. the induced emf in the loop at an instant when its side is a is
View SolutionA conducting square loop is placed in a magnetic field B with its plane perpendicular to the field. Now the sides of the loop start shrinking at a constant rate α. the induced emf in the loop at an instant when its side is a is
View SolutionA wire cd of length l and mass m is sliding without friction on conducting rails ax and by as shown. The verticle rails are connected to each other with a resistance R between a and b. A uniform magnetic field B is applied perpendicular to the plane abcd such that cd moves with a constant velocity of

View Solution
