
Find the common acceleration and tension in each string.

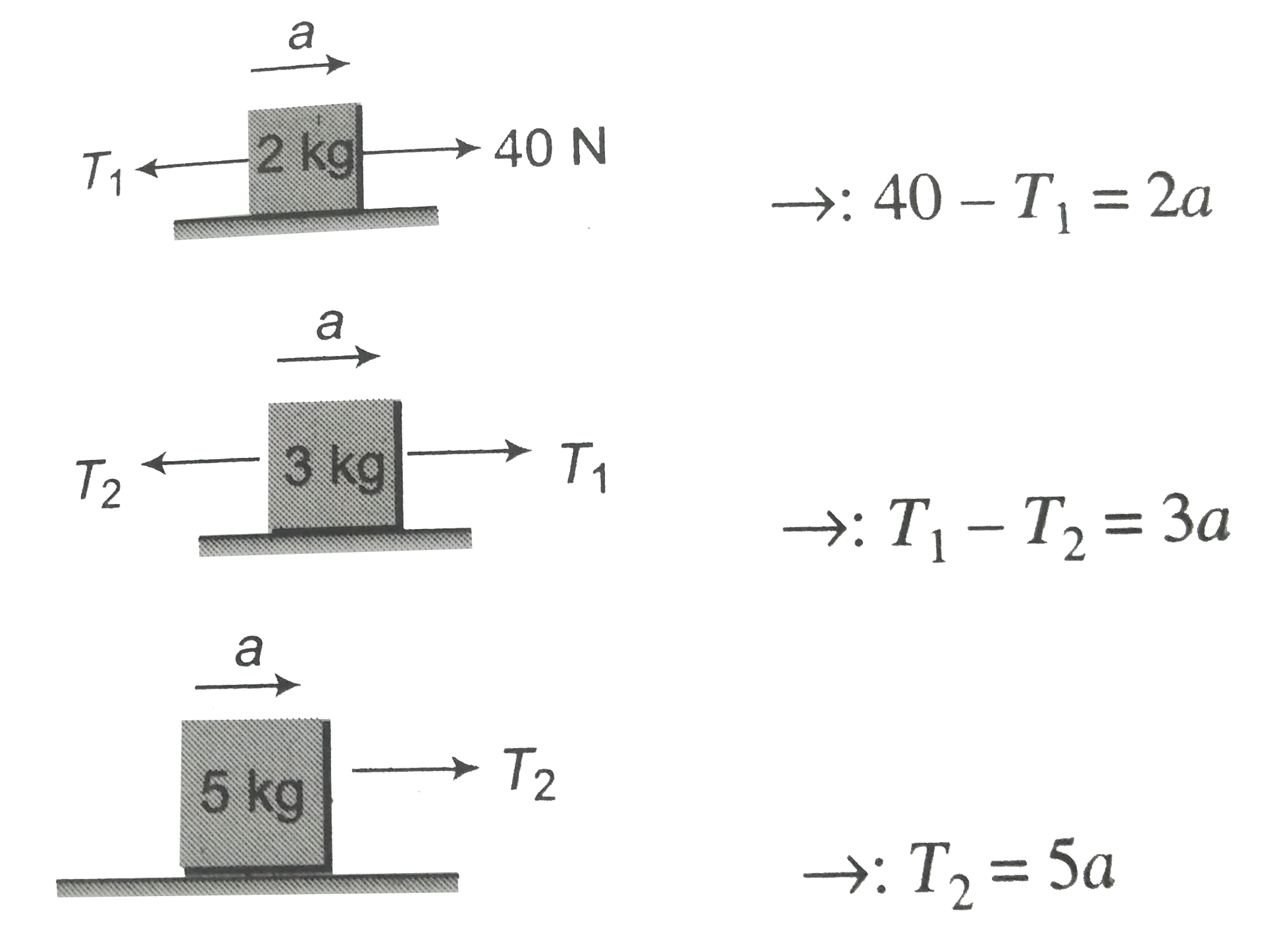 →:40−T1=2a
→:40−T1=2a
→:T1−T2=3a
→:T2=5a
Adding (i), (ii) and (III) we get
40=10a⇒a=4m/s2
T1=32N
T2=20N
Topper's Solved these Questions
Similar Questions
The blocks are attached by an inextensible light string and pulled vertically upward by force 100N as shows. Find the common acceleration and tension in the string

View SolutionThe blocks of masses 2kg,3kg and 5kg are connected by light inextensible strings as shown. The system of blocks is raised vertically upwards by appling a force F0=200N. Find the common acceleration and tensions in the strings.

View Solution
Knowledge Check
A system is at rest as shown in figure. The tension in the string in T1. When the 2 kg block is removed, the system moves with some acceleration a and tension in string becomes T2 Find T1/T2 .
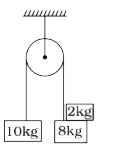 A98B109C911D119
A98B109C911D119The tension in the string is:
A29.4 NB39.2 NC58.8 ND88.2 NA pendulum bob is hanging from the roof of an elevator with the help of a light string. When the elevator moves up with uniform acceleration 'a' the tension in the string is T1.When the elevator moves down with the same acceleration, the tension in the string is T1 .If the elevator were stationary, the tension in the string would be
AT1+T22B√T1+T2CT1T2T1+T2D2T1T3T1+T2
In the above example, if two blocks have masses 1kg and 2kg respectively then find their acceleration and tension in different string.
View SolutionFind the acceleration and tension in the string in the following cases . The pulley and string are massless.
(a)
(b)
View SolutionTwo blocks are connected by an inextensible light string, the string is passing over smooth, light pulley as shown. Find the acceleration of blocks and tension in the string, reaction in pulley.

View SolutionConsider the situation shown in the figure. The surface is smooth and the string and the pulley are light. Find the acceleration of each block and tension in the string.

View SolutionTwo blocks are attached by a light inextensible string and the system is pulled by applying a force F0 as shown in the diagram. Find the acceleration of each block and tension in the string.

View Solution