n moles of an ideal gas undergo a process in which the temperature changes with volume as T=kv2. The work done by the gas as the temperature changes from 70 to 470 is
3nRT0
(52)nRT0
(32)nRT0
Zero
The correct Answer is:C
To solve the problem of finding the work done by an ideal gas as the temperature changes from 7∘C to 47∘C with the relationship T=kV2, we can follow these steps:
Step 1: Identify the relationship between temperature and volume
Given the equation T=kV2, we can express the volume in terms of temperature:
V=√Tk
Step 2: Differentiate the temperature with respect to volume
To find the work done, we need to express the work done dW in terms of volume. The differential form of the temperature is:
dT=2kVdV
From this, we can express dV in terms of dT:
dV=dT2kV
Step 3: Use the ideal gas law
According to the ideal gas law, we have:
PV=nRT
From the relationship T=kV2, we can substitute T into the ideal gas law:
P=nR(kV2)V=nRkV
Step 4: Express work done dW
The work done by the gas during an infinitesimal expansion is given by:
dW=PdV=nRkVdV
Substituting dV from the previous step:
dW=nRkV(dT2kV)=nR2dT
Step 5: Integrate to find total work done
Now we need to integrate dW from the initial temperature T1=7∘C to the final temperature T2=47∘C:
W=∫T2T1nR2dT=nR2(T2−T1)
Substituting the values:
W=nR2(47−7)=nR2×40=20nR
Final Answer
Thus, the work done by the gas as the temperature changes from 7∘C to 47∘C is:
W=20nR
Given the equation T=kV2, we can express the volume in terms of temperature:
V=√Tk
To find the work done, we need to express the work done dW in terms of volume. The differential form of the temperature is:
dT=2kVdV
From this, we can express dV in terms of dT:
dV=dT2kV
According to the ideal gas law, we have:
PV=nRT
From the relationship T=kV2, we can substitute T into the ideal gas law:
P=nR(kV2)V=nRkV
The work done by the gas during an infinitesimal expansion is given by:
dW=PdV=nRkVdV
Substituting dV from the previous step:
dW=nRkV(dT2kV)=nR2dT
Now we need to integrate dW from the initial temperature T1=7∘C to the final temperature T2=47∘C:
W=∫T2T1nR2dT=nR2(T2−T1)
Substituting the values:
W=nR2(47−7)=nR2×40=20nR
Thus, the work done by the gas as the temperature changes from 7∘C to 47∘C is:
W=20nR
Topper's Solved these Questions
Similar Questions
In a certain thermodynamical process, the pressure of a gas depends on its volume as kV3. The work done when the temperature changes from 100∘C to 300∘C will be x times nR, where n denotes number of moles of a gas. Find x.
View SolutionOne mole of an ideal gas undergoes a cyclic change ABCD. From the given diagram calculate the net work done in the process.
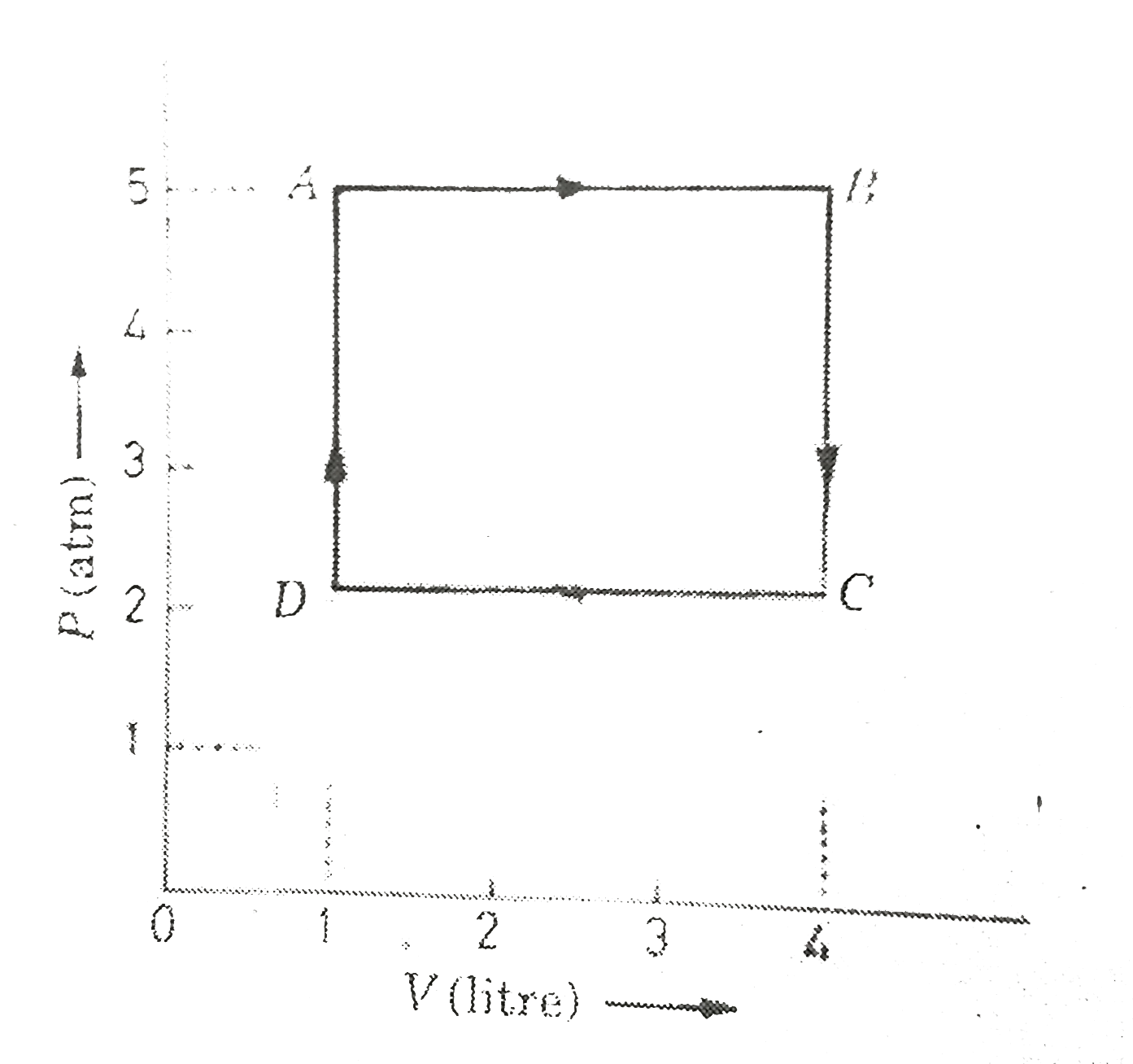
View Solution
Knowledge Check
n moles of an ideal triatomic linear gas undergoes a process in which the temperature changes with volume as 'T'=K_(1)V^(2)wherek_(1) is a constant. Choose incorrect alternative.
AAt normal temperature Cv=52RBAt any temperature Cp−Cv=RCAt normal temperature molar heat capacity C=3RDAt any temperature molar heat capacity C=3RTwo moles of helium gas undergo a cyclic process as shown in figure. Assuming the gas to be ideal. The net work done by the gas is
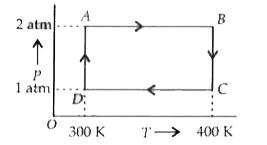 A200 Rln2B100 Rln2C300 Rln2D400 Rln2
A200 Rln2B100 Rln2C300 Rln2D400 Rln2n' moles of an ideal gas undergoes a process A→B as shown in the figure. The maximum temperature of the gas during the process will be:
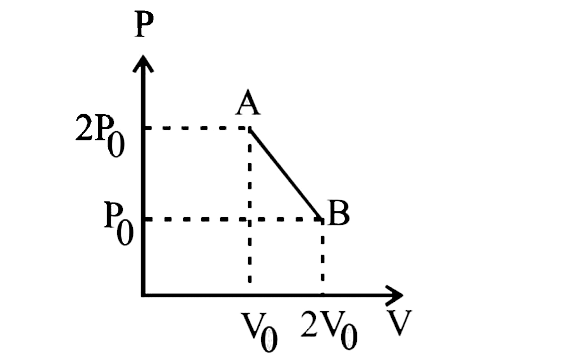 A9P0V02nRB9P0V0nRC9P0V04nRD3P0V02nR
A9P0V02nRB9P0V0nRC9P0V04nRD3P0V02nR
Three moles of an ideal gas undergo a cyclic process shown in figure. The work done by the gas during the process is [Take ln (2)=0.693]
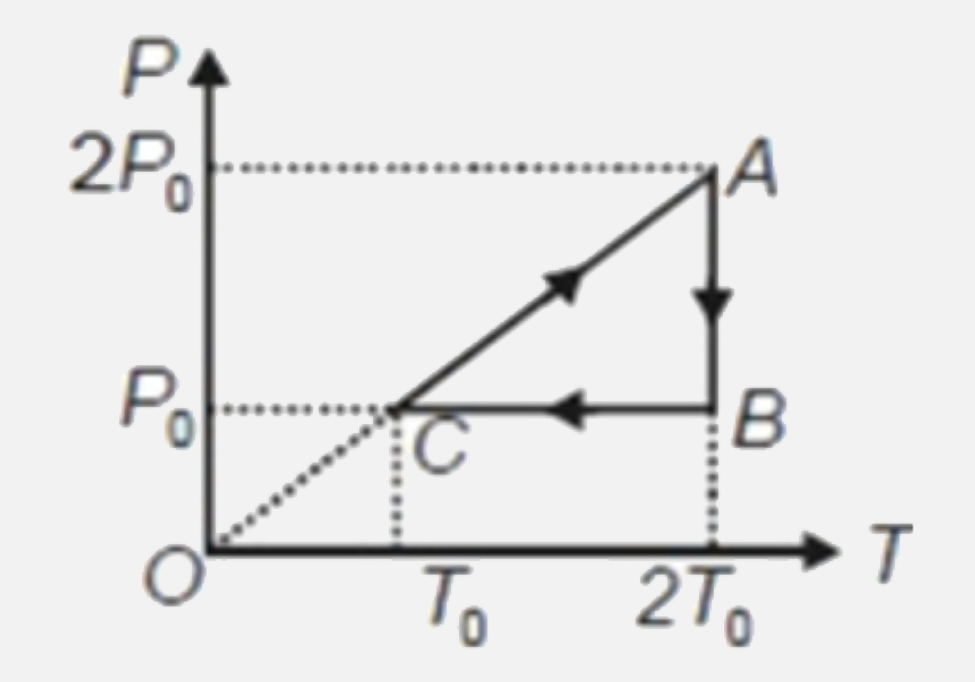
View SolutionOne mole of diatomic ideal gas undergoing a process in which absolute temperature is directely proportional to cube of volume, then, heat capacity of process is :
View SolutionOne mole of an ideal gas undergoes a process whose molar heat capacity is 4R and in which work done by gas for small change in temperature is given by the relation dW=2RdT, then find the degree of freedom of gas
View SolutionOne mole of an ideal gas undergoes an isothermal change at temperature 'T' so that its voume V is doubled. R is the molar gas constant. Work done by the gas during this change is
View SolutionOne mole of an ideal monotomic gas undergoes a linear process from A to B in which its pressure p and its volume V change as shown in figure.
The absolute temperature T versus volume V for the given process is
View Solution

