A monoatomic gas undergoes a process given by 2dU+3dW=0, then what is the process
To solve the problem regarding the process undergone by a monoatomic gas described by the equation 2dU+3dW=0, we will follow these steps:
1. Understanding the Given Equation:
The equation 2dU+3dW=0 can be rearranged to express dW in terms of dU:
3dW=−2dU⟹dW=−23dU
2. Applying the First Law of Thermodynamics:
The first law of thermodynamics states:
dQ=dU+dW
Substituting the expression for dW into the first law gives:
dQ=dU−23dU=13dU
3. Relating Change in Internal Energy to Temperature:
For a monoatomic ideal gas, the change in internal energy dU is related to the change in temperature dT by:
dU=CVdT
where CV for a monoatomic gas is 32R. Thus,
dU=32RdT
4. Substituting into the Heat Equation:
Now substituting dU into the equation for dQ:
dQ=13(32RdT)=12RdT
5. Identifying the Heat Capacity:
The expression for dQ can be compared to the general form:
dQ=CdT
From our earlier result, we see that:
C=12R
6. Determining the Type of Process:
The molar heat capacity C=12R indicates that this process does not correspond to isothermal (infinite heat capacity), isobaric (which would be CP=52R), or adiabatic (zero heat capacity). Instead, it corresponds to a polytropic process.
Conclusion:
The process described by the equation 2dU+3dW=0 is a polytropic process.
---
The equation 2dU+3dW=0 can be rearranged to express dW in terms of dU:
3dW=−2dU⟹dW=−23dU
The first law of thermodynamics states:
dQ=dU+dW
Substituting the expression for dW into the first law gives:
dQ=dU−23dU=13dU
For a monoatomic ideal gas, the change in internal energy dU is related to the change in temperature dT by:
dU=CVdT
where CV for a monoatomic gas is 32R. Thus,
dU=32RdT
Now substituting dU into the equation for dQ:
dQ=13(32RdT)=12RdT
The expression for dQ can be compared to the general form:
dQ=CdT
From our earlier result, we see that:
C=12R
The molar heat capacity C=12R indicates that this process does not correspond to isothermal (infinite heat capacity), isobaric (which would be CP=52R), or adiabatic (zero heat capacity). Instead, it corresponds to a polytropic process.
The process described by the equation 2dU+3dW=0 is a polytropic process.
Topper's Solved these Questions
- KINETIC THEORY OF GASESBook:NARAYNAChapter:KINETIC THEORY OF GASESExercise:C.U.Q
Explore 153 Videos
- KINETIC THEORY OF GASESBook:NARAYNAChapter:KINETIC THEORY OF GASESExercise:LEVEL-I(C.W)
Explore 32 Videos
- KINETIC THEORY OF GASESBook:NARAYNAChapter:KINETIC THEORY OF GASESExercise:LEVEL-I (H.W)
Explore 12 Videos
- GRAVITATIONBook:NARAYNAChapter:GRAVITATIONExercise:EXERCISE -IV
Explore 40 Videos
- LAW OF MOTIONBook:NARAYNAChapter:LAW OF MOTIONExercise:EXERCISE - IV
Explore 35 Videos
Similar Questions
A monoatomic gas undergoes a process in which the pressure (P) and the volume (V) of the gas are related as PV−3=constant. What will be the molar heat capacity of gas for this process?
View SolutionA monatomic ideal gas undergoes the shown cyclic process in which path of the process 2→3 is a semicircle. If 2mol of gas is taken, find

Heat given to the system in semicirculat process
View Solution
Knowledge Check
A certain amount of ideal monoatomic gas undergoes a process given by TV1/2= constant. The molar specific heat of the gas for the process will be given by
AR/2B−3R/2C3R/2D−R/2A monoatomic ideal gas undergoes a process ABC. The heat given to the gas is
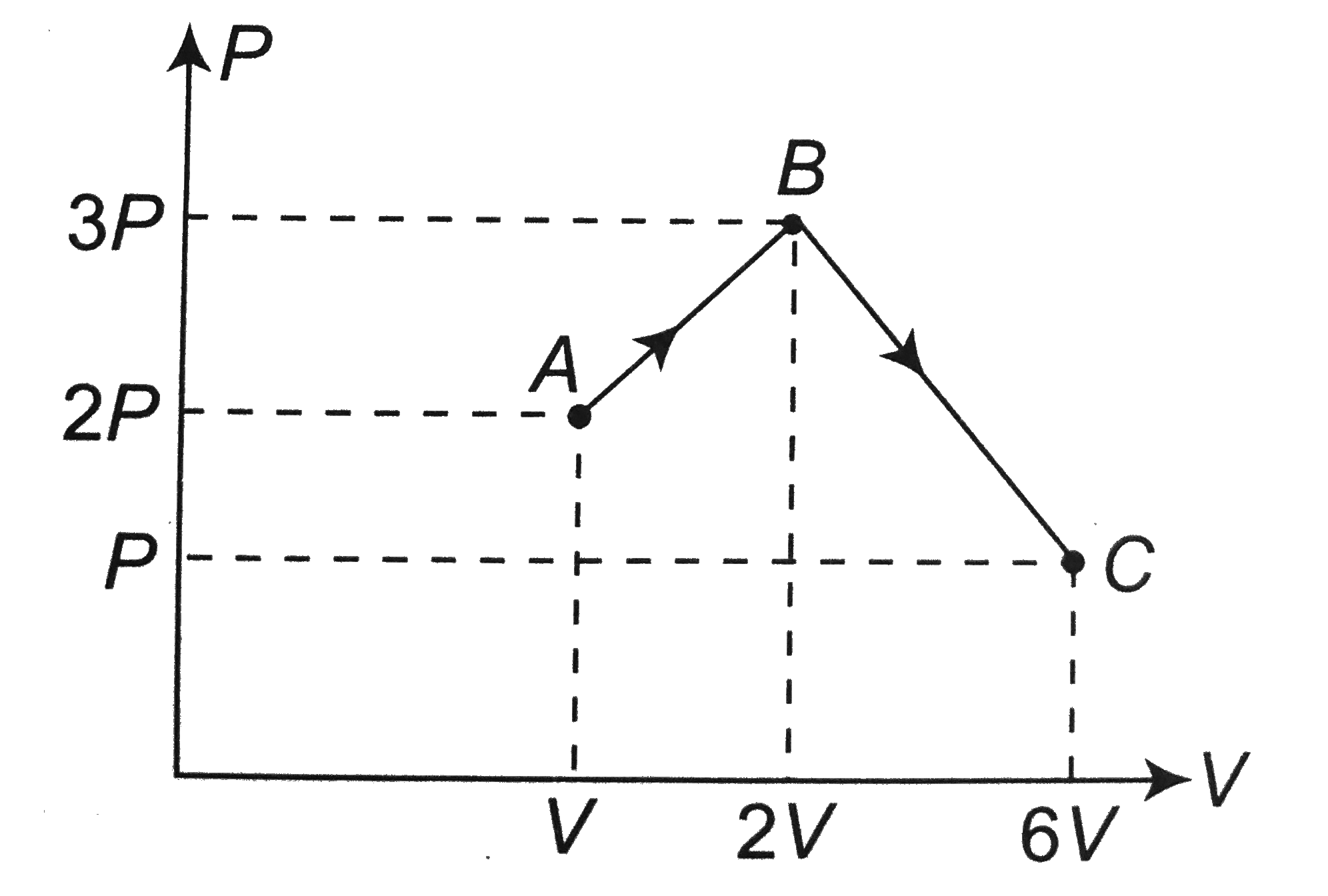 A7.5PVB12.5PVC16.5PVD20.5PV
A7.5PVB12.5PVC16.5PVD20.5PVOne mole of a monoatomic ideal gas undergoes process AB in given P – V diagram then average specific heat for this process is:
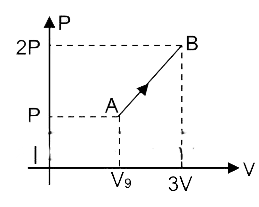 A21R10B18R10C9R10D13R10
A21R10B18R10C9R10D13R10
One mole of an ideal monoatomic gas undergoes a process as shown in the figure. Find the molar specific heat of the gas in the process.
R is a gas constant.
View Solution2 moles of an ideal monoatomic gas undergoes a cyclic process ABCA as shown in the figure. R is the univers l gas constant. (given ln 2=0.693) Answer the following questions
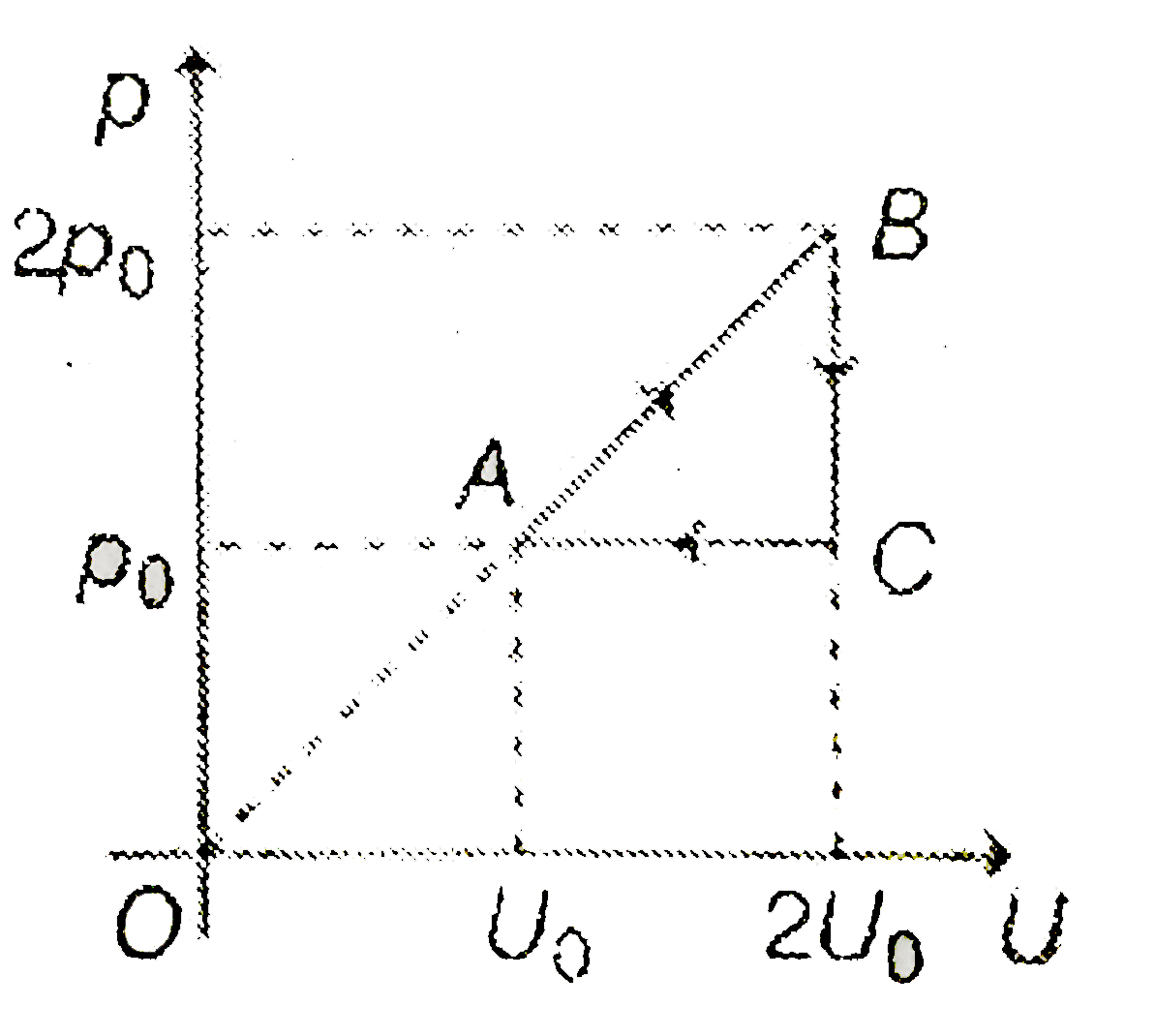
Percentage efficiency of the cycle is (approximately)
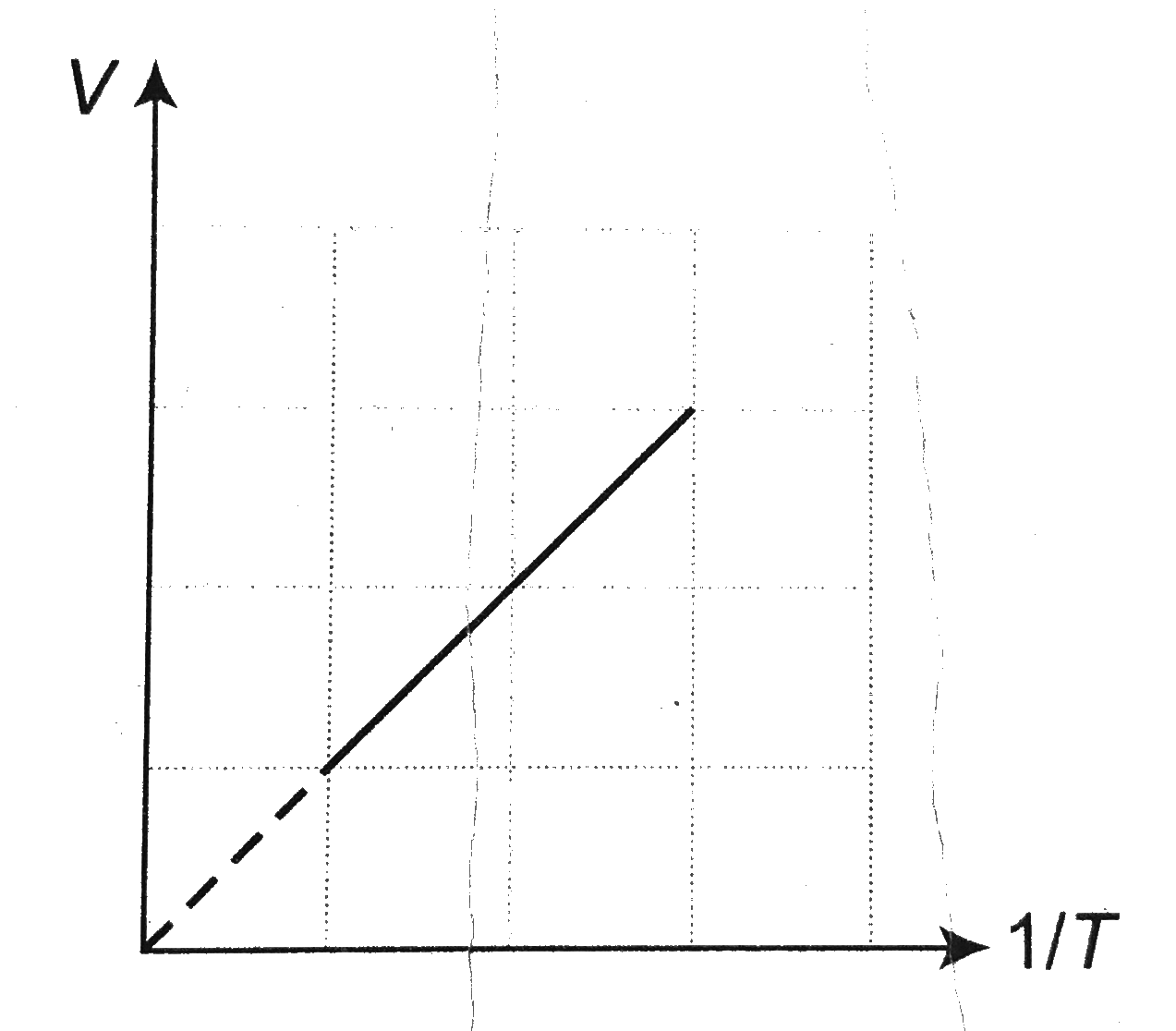
View SolutionOne mole of monoatomic gas undergoes a process as shown in the P-T diagram below. Choose the corresponding V – T diagram.
View Solution2 moles of an ideal monoatomic gas undergoes a cyclic process ABCA as shown in the figure. R is the univers l gas constant. (given ln 2=0.693) Answer the following questions

Graph of pressure versus volume of the cyclic process ABCA is
View SolutionA monoatomic ideal gas undergoes a process in which the ration of P to V at any instnat is constnat and equal to unity The molar heat capacity of gas is .
View Solution

