Water in a canal, 30 dm wide and 12dm deep, is flowing with a velocity of 20km per hour. How many area will it irrigate in 30min, if 9 cm of standing water is desired?
Answer:
Velocity of water=20Kmh
Water in the canal forms a cuboid of breadth =12dm=1210m=1.2m
Height =30dm=3010m=3m
Length = Distance covered by water in 30 minutes
=Velocity of water xx time
=20000×3060=10000m
Therefore,
Volume of water flown in 30 min = lbh=(1.2×3×10000)=36000m3
Suppose area irrigated be Am2. Then,
A×9100= Volume flown in 30 minutes
A×9100=36000
A=400000m2
Hence, area irrigated =400000m2
Topper's Solved these Questions
Similar Questions
Water in a canal, 30dmwidand12dmdeep , is flowing with a velocity of 20kmpeρur. How much area will it irrigate in 30m∈, if 9cm of standing water is desired?
View SolutionWater in a canal 30 dm wide and 12 dm deep, is flowing with a velocity of 100 km per hour. How much area will it irrigate in 30 minutes if 8cm of standing water is desired?
View Solution
Knowledge Check
Water in a canal 3 m wide and 1.2 m deep,is flowing with the velocity of 10 km/h. how mucharea (in hectares) will it irrigate in half an hour, if 9 cm of standing water is needed?
A20B18.8C21D20.4a D E D i G m G q J ? ?
AU JBt JCT JDu JIf a, b, c, d, e, f are A.M's between 2 and 12, then a + b + c + d + e + f is equal to
A14B42C84Dnone of these
Water in a canal, 6 m wide and 1.5 m deep, is flowing with a speed of 10 km/h. How much area will it irrigate in 30 minutes, if 8 cm of standing water is needed?
View SolutionWater flows in a tank 150mxx100m at the base, through a pipe whose cross-section is 2dmby1.5dm at the speed f 15kmperhour . In what time, will the water be 3metresdeep?
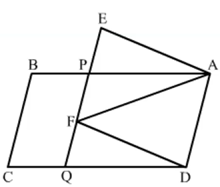
View SolutionIn Figure ABCDandAEFD are two parallelograms. Prove that: PE=FQ
View SolutionIn a triangle, P, Q and R are the mid-points of sides BC, CA and AB respectively. If AC=21 cm, BC=29cm and AB=30cm, find the perimeter of the quadrilateral ARPQ
View SolutionIn Fig 31, ABCD is a rectangle with dimensions 32 m by 18 m. ADE is a triangle such that EF⊥AD and EF=14 cm. Calculate the area of the shaded region.
View Solution
