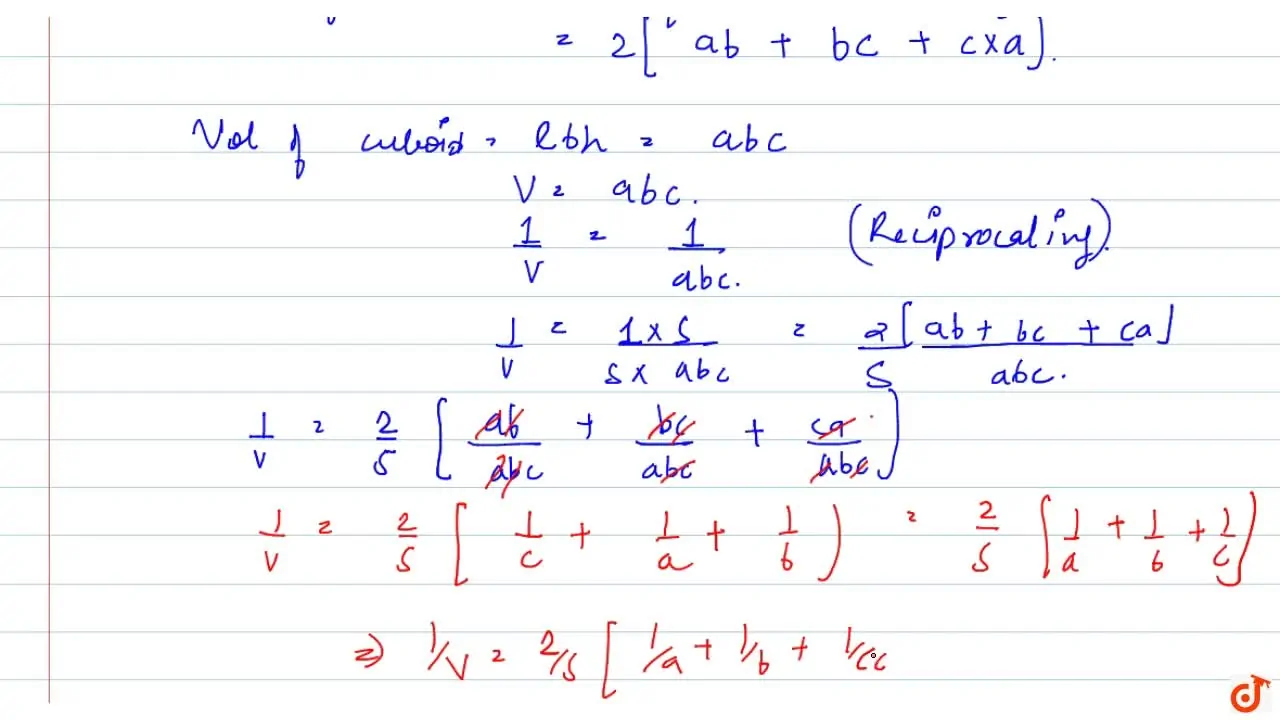If V is the volume of a cuboid of dimensions a, b, c and S is its surface area, then prove that 1V=2S(1a+1b+1c)
Volume of a cuboid =l×b×h
Surface area of cuboid=2(lb×bh×hl)
∴ 2s(1l+1b+1h)=2sbh+lh+lblbh
2s(1a+1b+1c)=2s(s2v)
On calculation
2s(1a+1b+1c)=1v
1v=2s(1a+1b+1c) Hence Proved.
Related Playlists
Similar Questions
If V is the volume of a cuboid of dimensions a, b, c and S is its surface area, then prove that 1V=2S(1a+1b+1c)
View SolutionIf V is the volume of a cuboid of dimensions a, b, c and S is its surface area, then prove that 1V=2S(1a+1b+1c)
View SolutionIf V is the volume of a cuboid of dimensions a,b,candS is its surface area, then prove that SV=2(1a+1b+1c)
View SolutionIf ‘V’ is the volume of a cuboid of dimensions a×b×cand ‘S’ is its surface area, then prove that
1V=25[1a+1b+1c].View SolutionIf V be the volume of the cuboid of dimensions a, b and c and S its total surface area, then 4S(1a+1b+1c) in terms of V is equal to
View SolutionIf V is the volume of a cuboid of dimensions x, y, z and A is its surface area, then AV (a) x2y2z2 (b) 12(1xy+1yz+1zx) (c) 2(1x+1y+1z) (d) 1xyz
View SolutionLet the dimensions of a cuboid be a, b and c. If v is volume and s is its surface area, then
1v=ks(1a+1b+1c). Value of k isView SolutionThe edges of a cuboid are in the ration 1:2:3 and its surface ara is 88cm2. The volume of the cuboid is
View SolutionThe dimension of a cuboid are 16 cm, 18 cm and 24 cm . Find :
(a) volume (b) surface area (c) diagonalView SolutionThe sum of length, breadth and height of a cuboid is 22 cm and the length of its diagonal is 14cm.
If S is the sum of the cubes of the dimensions of the cuboid and V is its volume, then what is (S - 3V) equal to?View Solution