The ratio in which the line segment joining points A(a1, b1) and B(a2, b2) is divided by y-axis is a1:a2 (b) a1:a2 (c) b1:b2 (d) −b1:b2
Step by step video & image solution for The ratio in which the line segment joining points A(a_1,\ b_1) and B(a_2,\ b_2) is divided by y-axis is a_1: a_2 (b) a_1: a_2 (c) b_1: b_2 (d) -b_1: b_2 by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
If the equation of the locus of a point equidistant from the points (a1,b1) and (a2,b2) is (a1−a2)x+(b2+b2)y+c=0, then the value of C is
Aa21−a22+b21−b22B√a21+b21−a22−b22C12(a21+a22+b21+b22)D12(a21+b22+a21+b22)The number of ways in which ten candidates A1,A2,....,A10 can be ranked so that A1 is always above A2 is
A10!2B10!C9!D8!2The capacitance of the capacitors of plate areas A1 and A2(A1<A2) at a distance d is
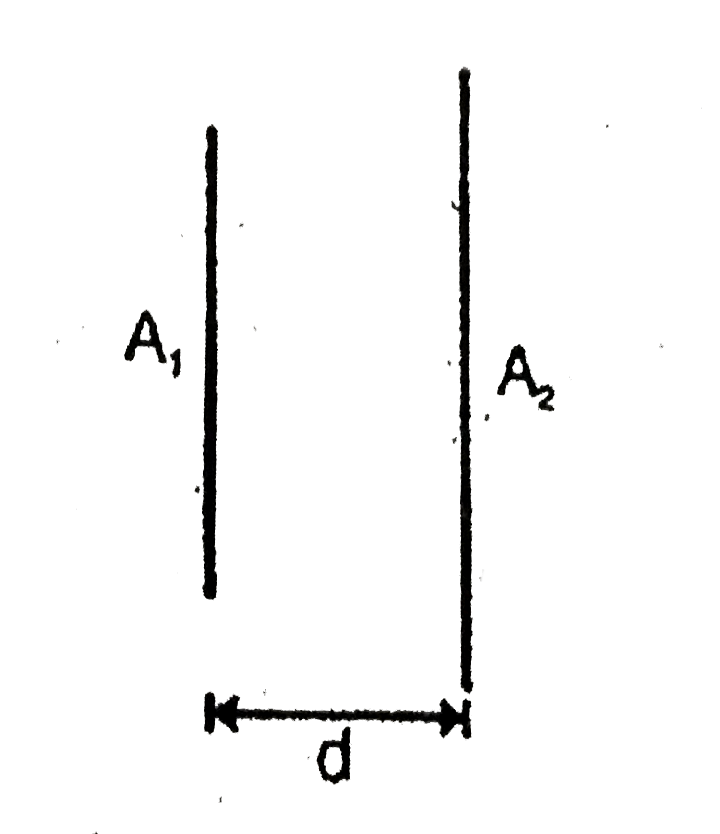 Aε0A1dBε0A2dCε0(A1+A2)2dDε0√A1A2d
Aε0A1dBε0A2dCε0(A1+A2)2dDε0√A1A2d
In direct proportion a1b1 = a2b2
View SolutionIf the line a1x+b1y+c1=0anda2x+b2y+c2=0 cut the coordinate axes in concyclic points, prove that : a1a2=b1b2.
View SolutionFor two linear equations , a1x+b1y+c1=0 and a2x+b2y+c2=0, the condition a1a2=b1b2=c1c2 is for.
View SolutionFind the coefficient of x in the determinant ∣∣ ∣ ∣∣(1+x)a1b1(1+x)a1b2(1+x)a1b3(1+x)a2b2(1+x)a2b2(1+x)a2b3(1+x)a3b3(1+x)a3b2(1+x)a3b3∣∣ ∣ ∣∣=0.
View SolutionLet bi>1 for i=1,2,....,101. Suppose logeb1,logeb2,....,logeb101 are in Arithmetic Progression (A.P.) with the common difference loge2. Suppose a1,a2,.....,a101 are in A.P. such that a1=b1anda51=b51. If t=b1+b2+....+b51and s=a1+a2+....+a51, then .
View Solution

