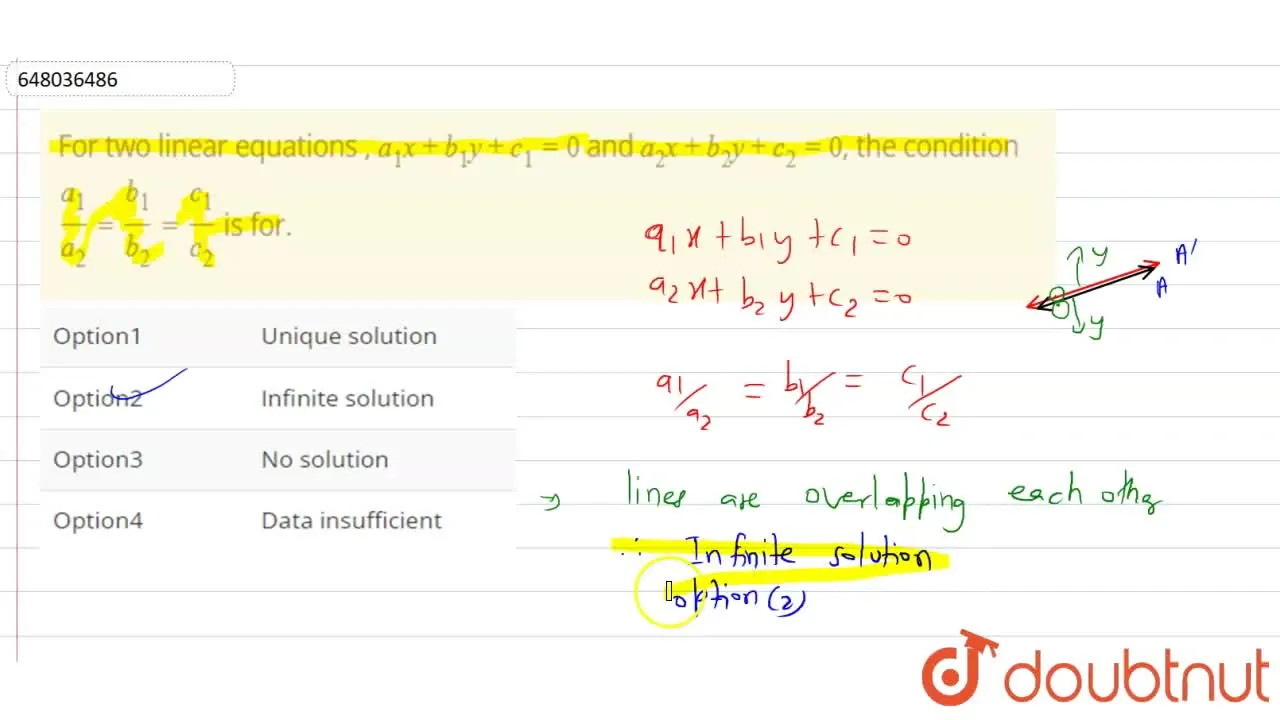
For two linear equations , $a_{1} x + b_{1} y + c_{1} = 0$ and $a_{2} x + b_{2} y + c_{2} = 0$ , the condition $\frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}} = \frac{c_{1}}{c_{2}}$ is for.

Unique solution

Infinite solution

No solution

Data insufficient

Video Solution

Text Solution

Generated By DoubtnutGPT

To solve the problem, we need to understand the condition given for the two linear equations:
1. Identify the equations:
The two linear equations are:
$a_{1} x + b_{1} y + c_{1} = 0 (1)$
$a_{2} x + b_{2} y + c_{2} = 0 (2)$
2. Understand the condition:
The condition provided is:
$\frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}} = \frac{c_{1}}{c_{2}}$
This condition indicates a specific relationship between the coefficients of the two equations.
3. Interpret the condition:
When the ratios of the coefficients of the two equations are equal, it implies that the two lines represented by these equations are not just parallel but actually coincide. This means they are the same line.
4. Conclusion about the lines:
Since the two lines are coincident, they overlap completely. Therefore, every point on one line is also a point on the other line.
5. Determine the number of solutions:
Because the two lines are the same, there are infinitely many solutions to the system of equations. Any point (x, y) that satisfies one equation will also satisfy the other.
6. Final answer:
Thus, the condition $\frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}} = \frac{c_{1}}{c_{2}}$ indicates that the two lines overlap, leading to infinitely many solutions.

Updated on:8/8/2024

If the equations $4 x + 6 y = 15 and 8 x + k y = 30$ have infinite solutions, then find the value of $k$ . The following are the steps involved in solving the above problem. Arrange them in sequential order.
(A) $\frac{4}{8} = \frac{6}{k} = \frac{- 15}{- 30} \Rightarrow \frac{6}{k} = \frac{1}{2}$
(B) We know that, if $a_{1} x + b_{1} y + c_{1} = 0 and a_{2} x + b_{2} y + c_{2} = 0$ have infinite solutions, then $\frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}} = \frac{c_{1}}{c_{2}}$ .
(C) Given that, $4 x + 6 y - 15 = 0 and 8 x + k y - 30 = 0$ have infinite solutions.
(D) $∴ k = 12$ .
ACBAD
BABCD
CCABD
DBDAC
Assertion (A) :Pair of linear equations $9 x + 3 y + 12 = 0$ and $18 x + 6 y + 24 = 0$ have infinitely many solutions
Reason (R ) : Pair of linear equations $a_{1} x + b_{1} y + c_{1} = 0$ and $a_{2} x + b_{2} y + c_{2} = 0$ have infinitely many solutions if $\frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}} = \frac{c_{1}}{c_{2}}$
ABoth A and R are true and R is the correct explanation for A.
BBoth A and R are true and R is not correct explanation for A.
CA is true but R is false
DA is false but R is true
If in equation $a_{1} x + b_{1} y + c_{1} = 0 and a_{2} x + b_{2} y + c_{2} = 0, \frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}$ then which of the following is true?
AUnique solution
BNo solution
CInfinite solution
DNone of these