The rate constant for the first order decomposition of H2O2 is given by the following equation :
logk=14.34−1.25×104K/T
Calculate Ea for this reaction and at what temperature will its half-period be 256 minutes ?
Step by step video & image solution for The rate constant for the first order decomposition of H_(2)O_(2) is given by the following equation : logk=14.34-1.25xx10^(4)"K"//"T" Calculate E_(a) for this reaction and at what temperature will its half-period be 256 minutes ? by Chemistry experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - PRADEEPCHAPTER - CHEMICAL KINETICSEXERCISE - ADVANCED PROBLEMS FOR COMPETITIONS14videos
CHEMICAL KINETICS
- BOOK - PRADEEPCHAPTER - CHEMICAL KINETICSEXERCISE - COMPETITION FOCUS (JEE(Main and Advanced)/Medical Entrance) (VIII. Multiple Choice Questions)3videos
CHEMICAL KINETICS
- BOOK - PRADEEPCHAPTER - BIOMOLECULES EXERCISE - IMPORTANT QUESTIONS (FOR BOARD EXAMINATION)25videos
BIOMOLECULES
- BOOK - PRADEEPCHAPTER - CHEMISTRY IN EVERYDAY LIFE EXERCISE - IMPORTANT QUESTION FOR BOARD EXAMINATION30videos
CHEMISTRY IN EVERYDAY LIFE
Similar Questions
The rate constant for the first order decomposition of H2O2 is given by the following equation :
logk=14.34−1.25×104K/T
Calculate Ea for this reaction and at what temperature will its half-period be 256 minutes?View SolutionThe rate constant for the first order decomposition of H2O2 is given by the following equation :
logk=14.2−1.0×104T
Calculate Ea for this reaction and rate constant k if its half-life period be 200 minutes.
[Given : R=8.314JK−1mol−1]View SolutionThe rate constant for the first order decomposition of H2O2 is given by the following equation : log K = 14.2 - 1.0×104TK
Calculate Ea for this reaction and rate constant k if its half life period be 200 minutes. (Given : R = 8.314 JK−1mol−1)View SolutionThe rate constant for the first order decomposition of N2O5 is given by the following equation: k=(2.5×1014s−1)e(−25000K)/T
Calculate Ea for this reaction and rate constant if its half-life period be 300 minutes.View SolutionThe rate constant for the first order decompoistion of a certain reaction is described by the equation
logk(s−1)=14.34−1.25×104KT
(a) What is the energy of activation for the reaction?
(b) At what temperature will its half-life periof be 256min?View SolutionThe rate constant for the first order decompoistion of a certain reaction is described by the equation
logk(s−1)=14.34−1.25×104KT
(a) What is the energy of activation for the reaction?
(b) At what temperature will its half-life periof be 256min?View SolutionThe rate constant for the first order decomposition of ethylene oxide into CH4 and CO,
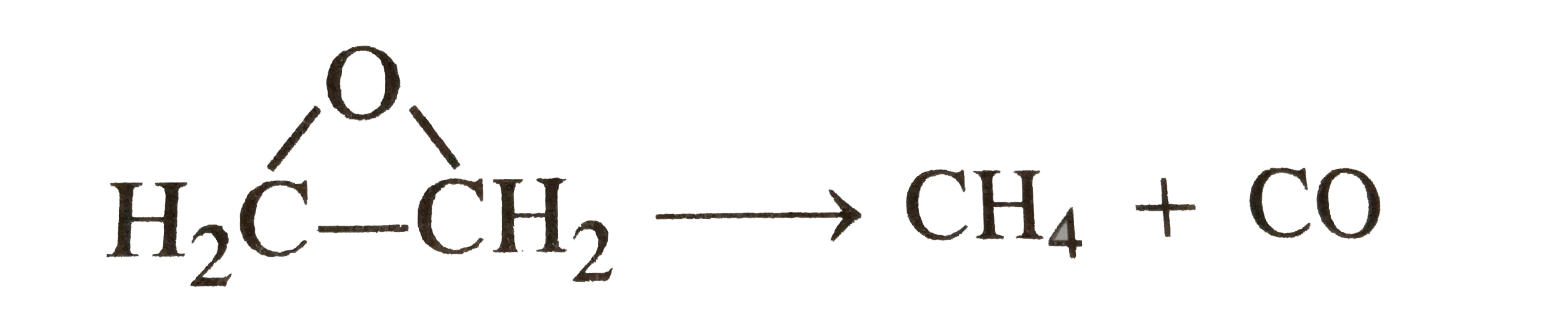
may be describe by
logk(ins−1)=14.34−1.25×104KT
The activation energy of the reaction isView SolutionThe rate constant of the first order reaction , that is decomposition of ethylene oxide into CH4 and CO, may be described by the following equation
logk(s−1)=14.34−1.25×104TK
rate constant at 397∘CView SolutionThe rate constant for the first order decomposition of N2O5 dissolved in chloroform at 45∘C is 3.1×10−4−1min
2N2O5→4NO2+O2
What is the rate of this reaction at (N2O5)=0.4MView SolutionThe rate constant of the first order reaction , that is decomposition of ethylene oxide into CH4 and CO, may be described by the following equation
logk(s−1)=14.34−1.25×104TK
Find (a) energy of activation ,View Solution


