One of the corner points of the feasible region of inequalities gives
Optimal solution of LPP
Objective function
Constraints
Linear assumptions
The correct Answer is:A
Step by step video, text & image solution for One of the corner points of the feasible region of inequalities gives by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- LINEAR PROGRAMMINGBOOK - TARGET PUBLICATIONCHAPTER - LINEAR PROGRAMMINGEXERCISE - Critical Thinking
28 Videos
- LINEAR PROGRAMMINGBOOK - TARGET PUBLICATIONCHAPTER - LINEAR PROGRAMMINGEXERCISE - Competitive Thinking
35 Videos
- LINEBOOK - TARGET PUBLICATIONCHAPTER - LINEEXERCISE - Evaluation Test
1 Videos
- MATHEMATICAL LOGIC BOOK - TARGET PUBLICATIONCHAPTER - MATHEMATICAL LOGIC EXERCISE - EVALUATION TEST
14 Videos
Similar Questions
Knowledge Check
Corner points of fealible region of inequalities gives
Aan optiomal solution of L.P.P.Ban objective functionCthe constraints.Dthe linear assumption.the corner points of the feasible region of a system of linear inequalities 3x+5y≤15,5x+2y≥10,x≥0,y≥0, are:
A(2,0),(2019,4519),(0,3)B(0,3),(2019,4519),(0,5)C(2,0),(2019,4519),(5,0)D(0,0),(2,0),(2019,4519),(0,3)The maximum or minimum of the objective funtion occurs only at the corner points of the feasible region. This theorem is known as fundamental theorem of
AAlgebraBArithmeticCCalculusDExtreme point
Find the corner points of the feasible region of the linear programming problem;, Max Z =x : Subject to the constraints 3x+2y≤12,2x+3y≤13,x≥0,y≥0
View SolutionIf 3x+4y≥12,2x+y≤6,x≥0,y≥0, then the corner points of the feasible region are
View SolutionConsider the following LPP:
Maximize Z=3x+2y subject to the constraints:
x+2y≤10,3x+y≤15,x,y≥0.
(a) Draw the feasible region.
(b)Find the corner points of the feasible region.
(c) Find the maximum value of Z.
View SolutionThe corner points of the feasible region of the system of linear inequations x+y≥2,x+y≤5,x−y≥0,x,y≥0 are :
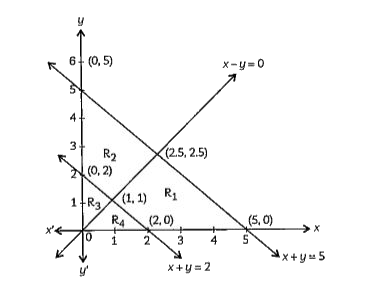
View SolutionThe corner points of the feasible region of a system of linear inequations are (0, 0), (5, 0), (6,5), (6, 8), (4, 10) and (0,8). If Z = 3x - 4y, then the minimum value of Z occurs at:
View Solution
