Find the value of three places of decimals, of each of following: It is given that $\sqrt{2} = 1.414, \sqrt{3} = 1.732, \sqrt{10} = 3.162$ and $\sqrt{5} = 2.236$ (approx). (i) $\frac{1}{\sqrt{2}}$ (ii) $\frac{1}{\sqrt{3}}$ (iii) $\frac{1}{\sqrt{10}}$

Video Solution

Text Solution

Verified by Experts

(i) Given :
$\frac{1}{\sqrt{2}}$
Multiplying the numerator and denominator of the given number by $\sqrt{2}$
i.e,
$\frac{1}{\sqrt{2}} = \frac{1}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}}$
$= \frac{\sqrt{2}}{2} = \frac{1.414}{2} = 0.707$
(ii) Given :
$\frac{1}{\sqrt{3}}$
Multiplying the numerator and denominator of the given number by $\sqrt{2}$
i.e,
$\frac{1}{\sqrt{3}} = \frac{1}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}$
$= \frac{\sqrt{3}}{3} = \frac{1.732}{3} = 0.577$
(iii) Given :
$\frac{1}{\sqrt{10}}$
Multiplying the numerator and denominator of the given number by $\sqrt{10}$
i.e,
$\frac{1}{\sqrt{10}} = \frac{1}{\sqrt{10}} \times \frac{\sqrt{10}}{\sqrt{10}}$
$= \frac{\sqrt{10}}{10} = \frac{3.162}{10} = 0.316$

Updated on:21/07/2023

|

Class 9 MATHS RATIONALISATION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Match the following if $\sqrt{2} = 1.414, \sqrt{3} = 1.732, \sqrt{5} = 2.236$ and $π = 3.141$ .

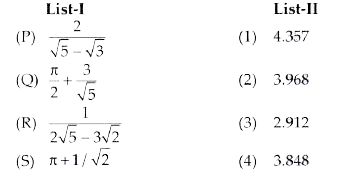AP-2, Q-3, R-1, S-4
BP-1, Q-2, R-3, S-4
CP-4, Q-1, R-2, S-3
DP-3, Q-1, R-2, S-4

RD SHARMA-RATIONALISATION -All Questions

Home
Ask Doubt
Profile