Given that : evaluate each of the following :
To evaluate the expression √1447, we can follow these steps:
Step 1: Simplify the expression
We start with the expression:
√1447=√144√7
Step 2: Calculate √144
Since 144 is a perfect square, we know:
√144=12
Step 3: Substitute the value of √7
From the given values, we have:
√7≈2.646
Now we can substitute this into our expression:
√144√7=12√7≈122.646
Step 4: Perform the division
Now we need to calculate 122.646:
122.646≈4.53
Final Answer
Thus, the value of √1447 is approximately:
4.53
---
We start with the expression:
√1447=√144√7
Since 144 is a perfect square, we know:
√144=12
From the given values, we have:
√7≈2.646
Now we can substitute this into our expression:
√144√7=12√7≈122.646
Now we need to calculate 122.646:
122.646≈4.53
Thus, the value of √1447 is approximately:
4.53
Topper's Solved these Questions
Similar Questions
Knowledge Check
Match the following if √2=1.414,√3=1.732,√5=2.236 and π=3.141 .
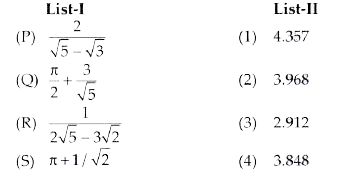 AP-2, Q-3, R-1, S-4BP-1, Q-2, R-3, S-4CP-4, Q-1, R-2, S-3DP-3, Q-1, R-2, S-4
AP-2, Q-3, R-1, S-4BP-1, Q-2, R-3, S-4CP-4, Q-1, R-2, S-3DP-3, Q-1, R-2, S-4
Given that √2=1.414, √3=1.732, √5=2.236 and √7=2.646, find the square roots of the following : 16975
View SolutionGiven that √2=1.414, √3=1.732, √5=2.236 and √7=2.646, find the square roots of the following : 27650
View SolutionGiven that √2=1.414, √3=1.732, √5=2.236 and √7=2.646, find the square roots of the following : 2565
View Solution√2=1.414 then 5√2=
View SolutionGiven that √2=1.414 and √5=2.236, evaluate each of the following √365 (ii) √62598
View SolutionGiven √2=1.414,√3=1.732,√5=2.236, find the value, correct to three decimals of the following
1−√3√5−√2
View SolutionIt being given that √2=1.414,√3=1.732,√5=2.236and√10=3.162, find the value to three places of decimials, of each of the following .
(i) 2√5 (ii) 2−√3√3 (iii) √10−√5√2
View Solution

