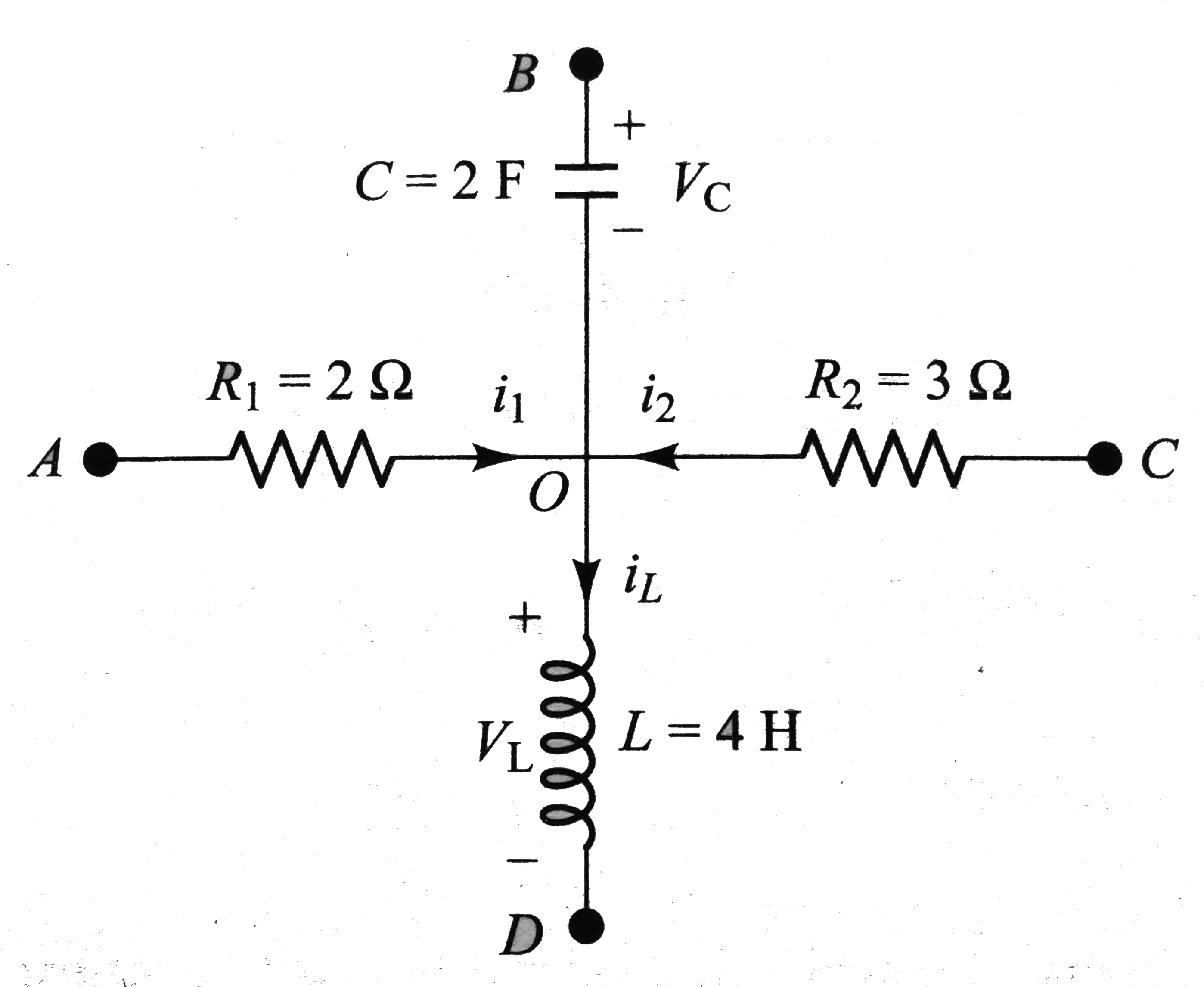
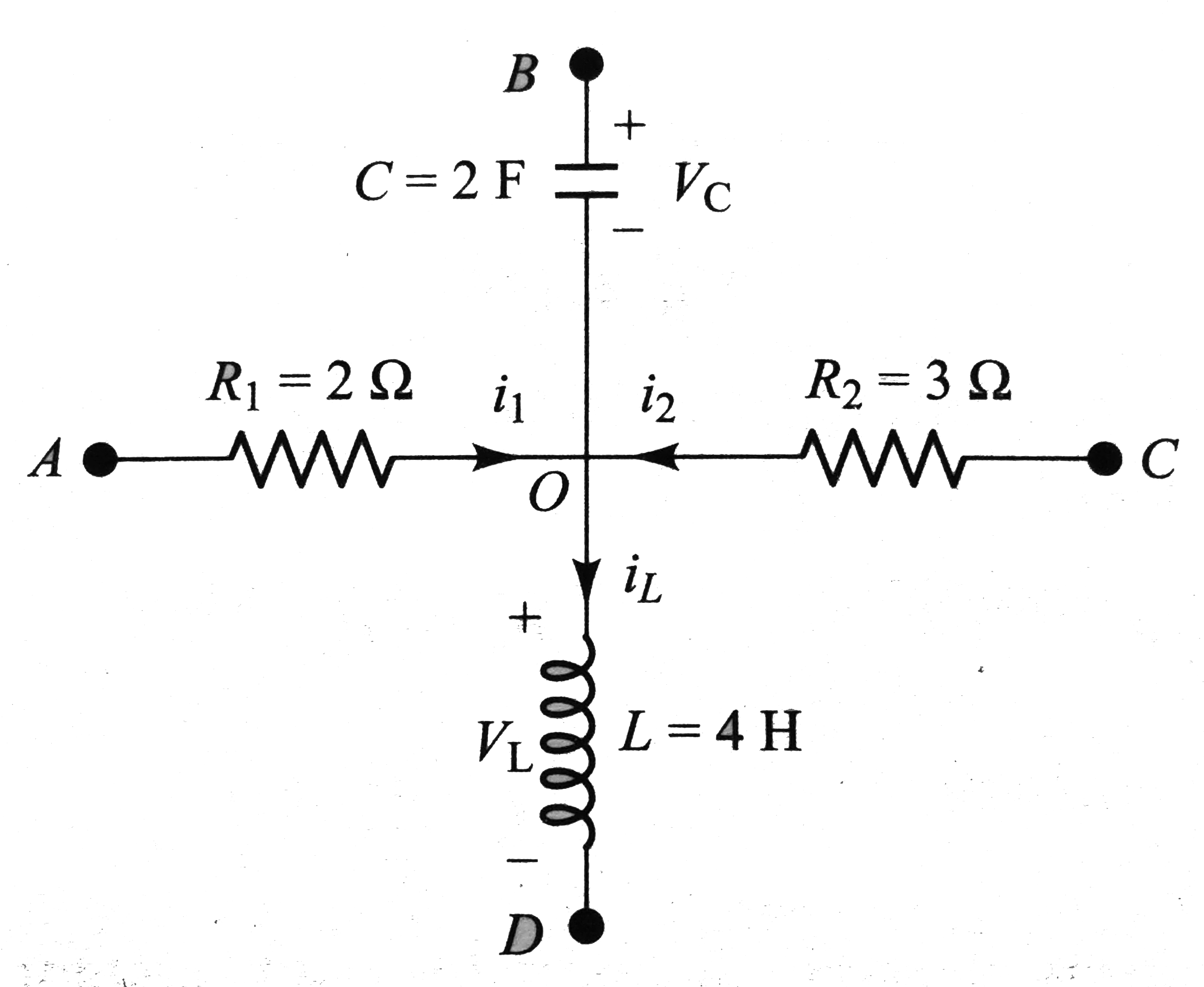
In figure i1=10e−2tA,i2=4A,vC=3e−2tV
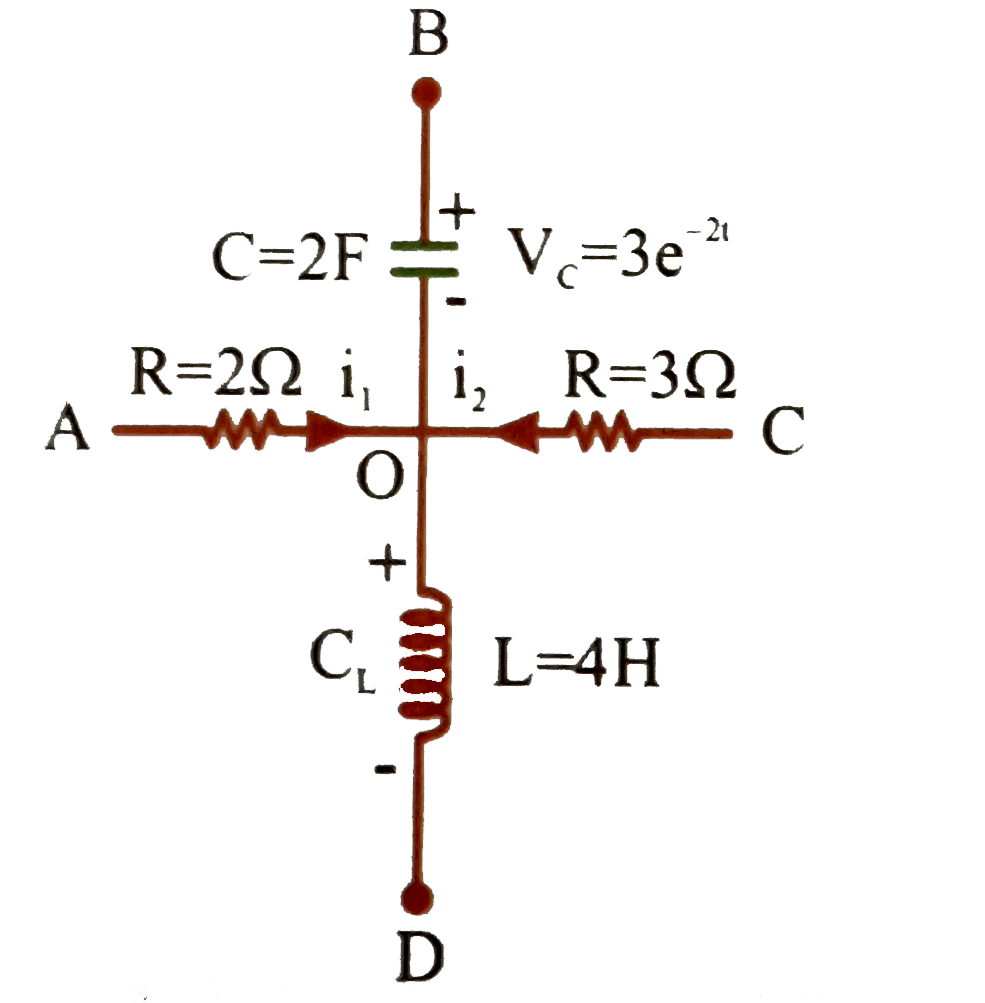
The variation of potential difference acorss A and C with time can be represented as
A
B

C
D

Video Solution
Text Solution
The correct Answer is:A
From KVL we have
VA−i1R1+i2R2=VC , VA−VC=i1R1−i2R2
Substituting the values, we have
VAC=(10e−2t)(2)−(4)(3)
VAC=(20e−2t−12)V
At t=0,VAC=8V, At t=∞,VAC=12V
Therefore, VAC decreases exponentially from 8V to - −12V
|
Topper's Solved these Questions
- ALTERNATING CURRENTBook:NARAYNAChapter:ALTERNATING CURRENTExercise:LEVEL - VI
Explore 120 Videos
- ALTERNATING CURRENTBook:NARAYNAChapter:ALTERNATING CURRENTExercise:LEVEL - I (H.W)
Explore 23 Videos
- ALTERNATING CURRENTBook:NARAYNAChapter:ALTERNATING CURRENTExercise:LEVEL - IV NCERT Based Questions
Explore 15 Videos
- ATOMIC PHYSICSBook:NARAYNAChapter:ATOMIC PHYSICSExercise:LEVEL-II (H.W)
Explore 14 Videos
Similar Questions
Knowledge Check
In Fig i1=10e−2tA, i2=4A, and VC=3e−2tV.
the vartiation of potential difference across A and C(VAC) with time can be respresented asA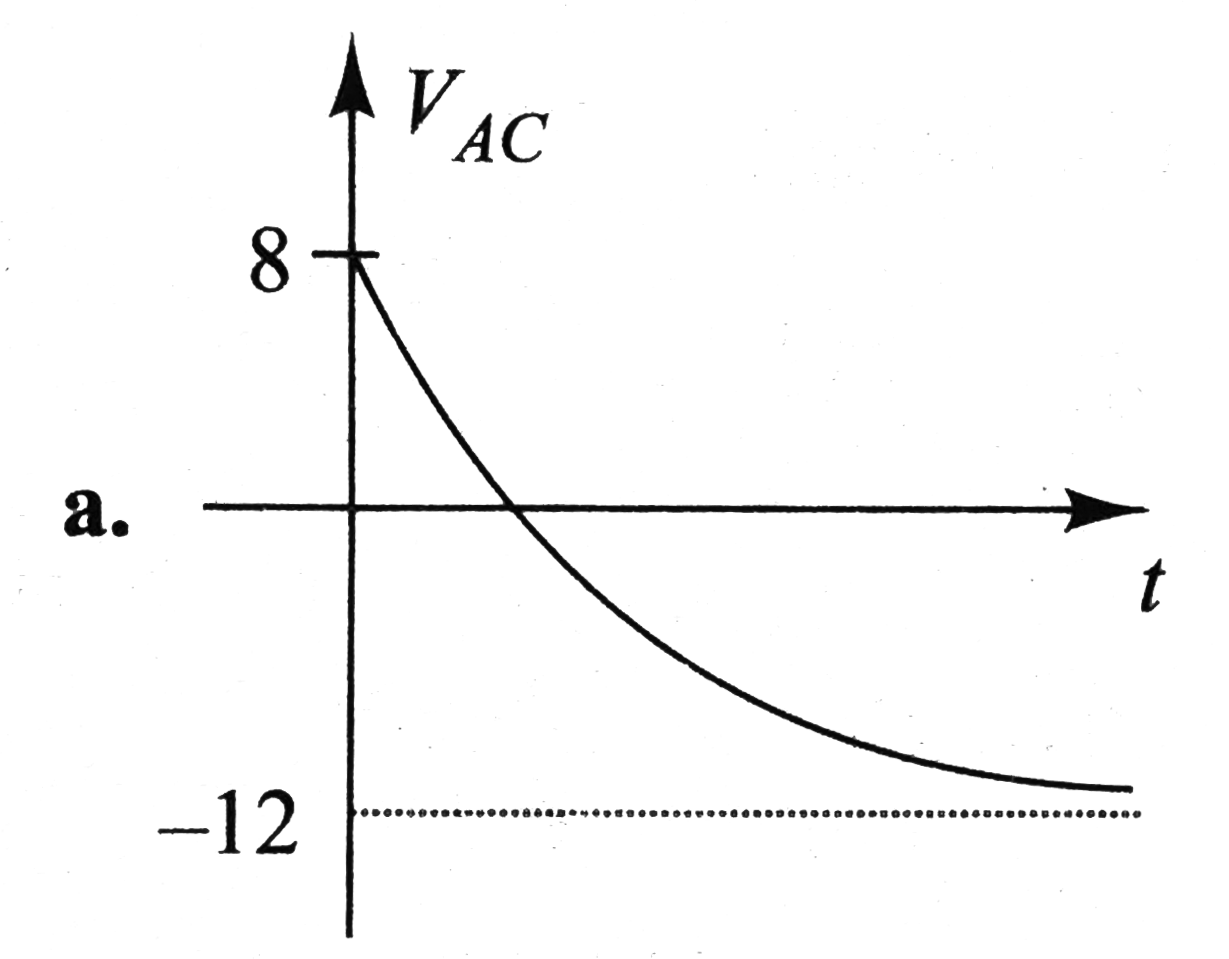 B
B C
C D
D
In Fig i1=10e−2tA, i2=4A, and VC=3e−2tV.
The variation of potential difference across C and D(VCD) with time can be expressed asA B
B C
C D
D
In figure i1=10e−2tA,i2=4A,vC=3e−2tV
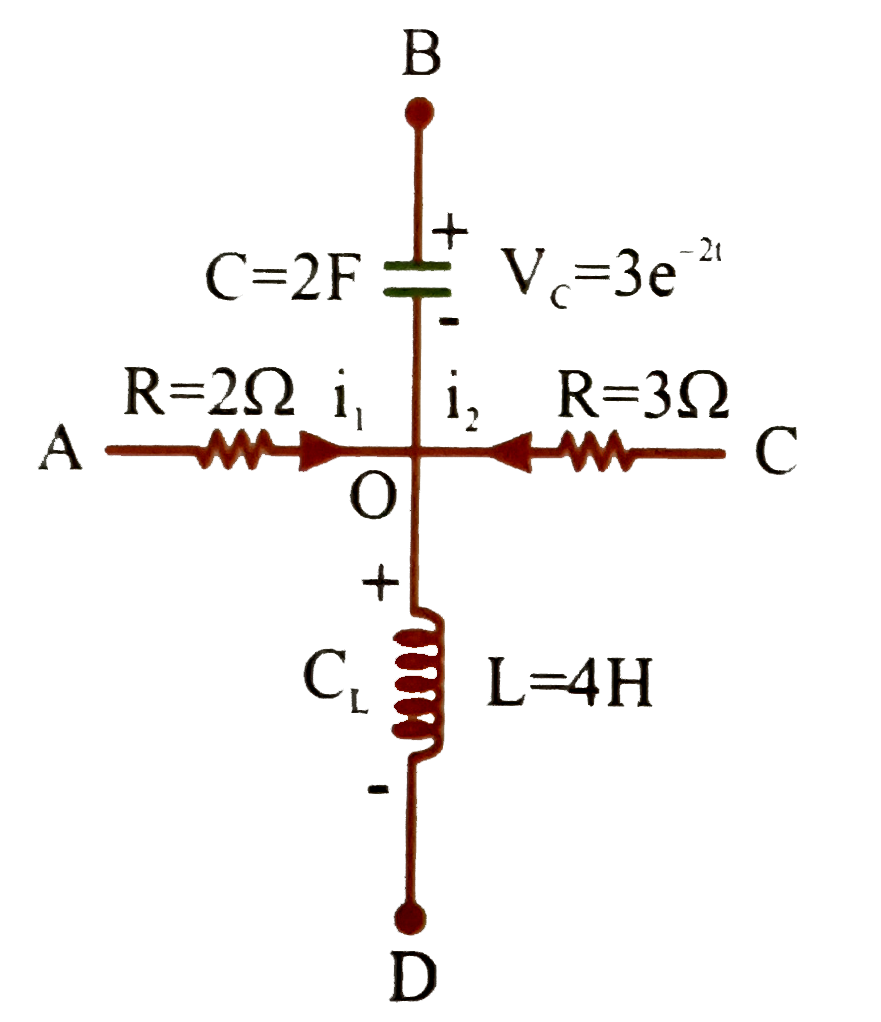
The current iL isA[2−2(1−e−2t)]AB[2+2(1−e−2t)]AC[3−2(1−e−2t)]AD[2+3(1−e−2t)]A
In the Figure shown i1=10e−2tA,i2=4A and VC=3e−2tV. Determine

a. iL and VL b. Vac,Vab,Vcd
View SolutionIn figure i1=10e−2tA,i2=4A,vC=3e−2tV
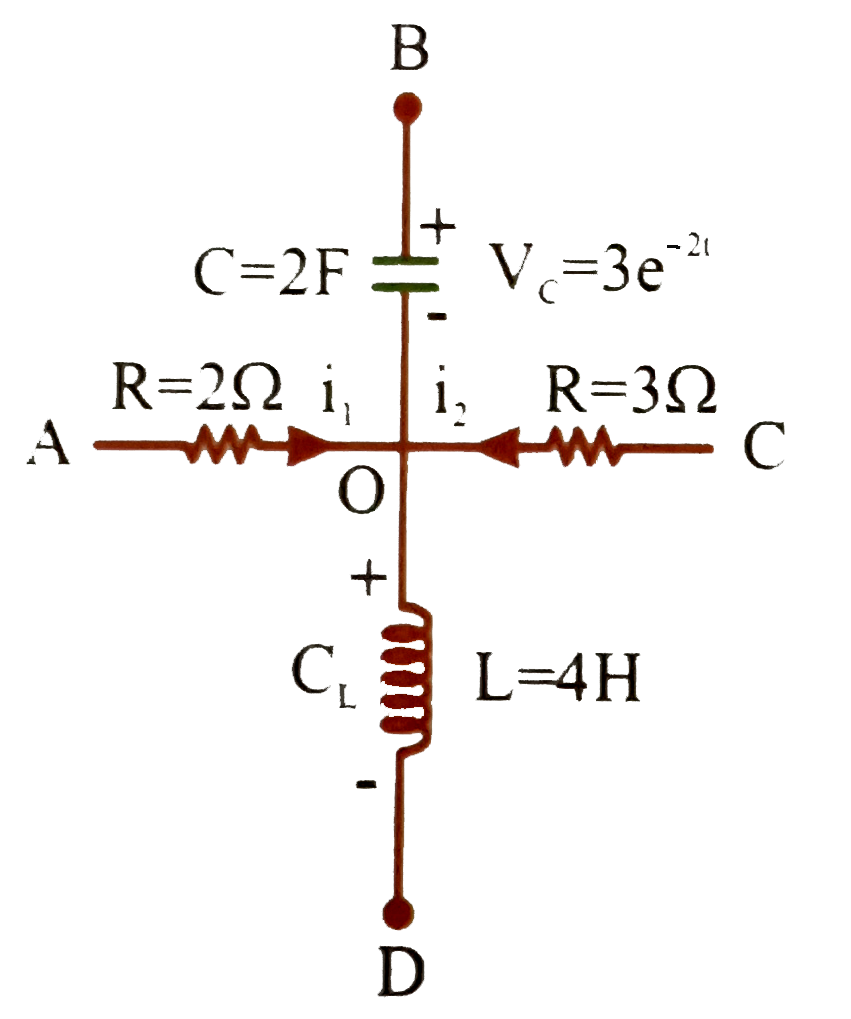
The potential difference across AB(VAB) is:
View SolutionIn figure i1=10e−2tA,i2=4A,vC=3e−2tV
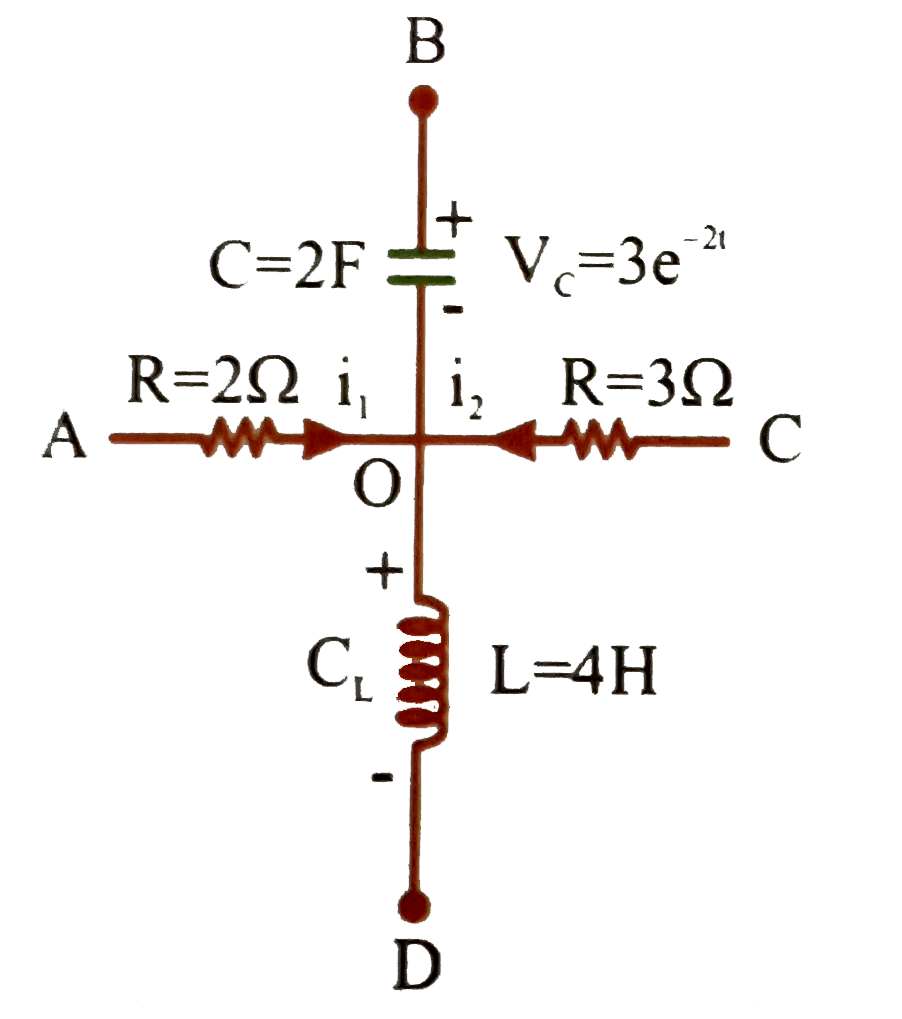
The potential difference across inductor VL is :
View SolutionIn Fig i1=10e−2tA, i2=4A, and VC=3e−2tV.
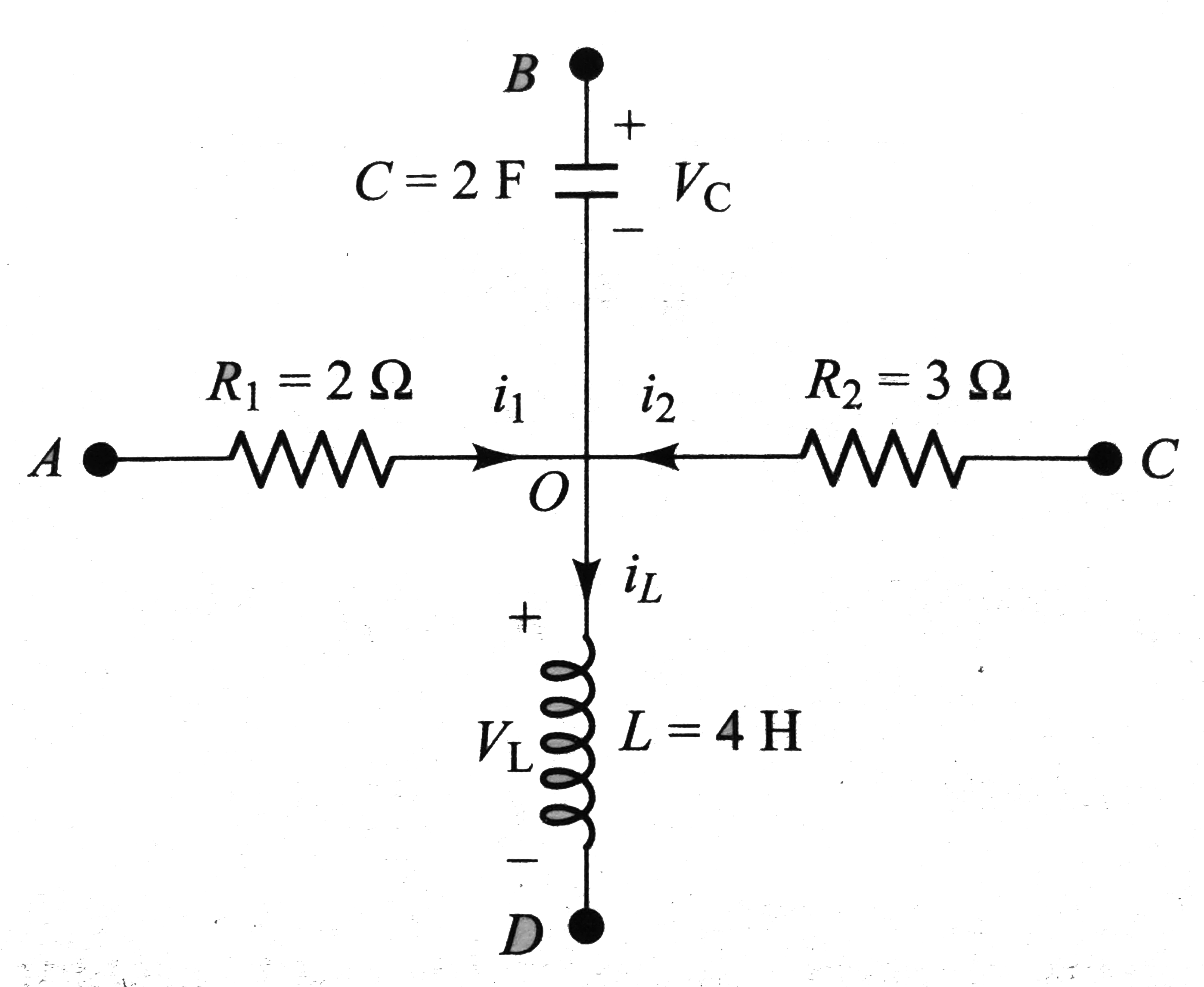
The variation of current in the inductor with time can be represented as
View SolutionIn figure i1=10e−2tA,i2=4A,vC=3e−2tV

The variaton of current in the inductor with time can be repesented as :
View Solution



