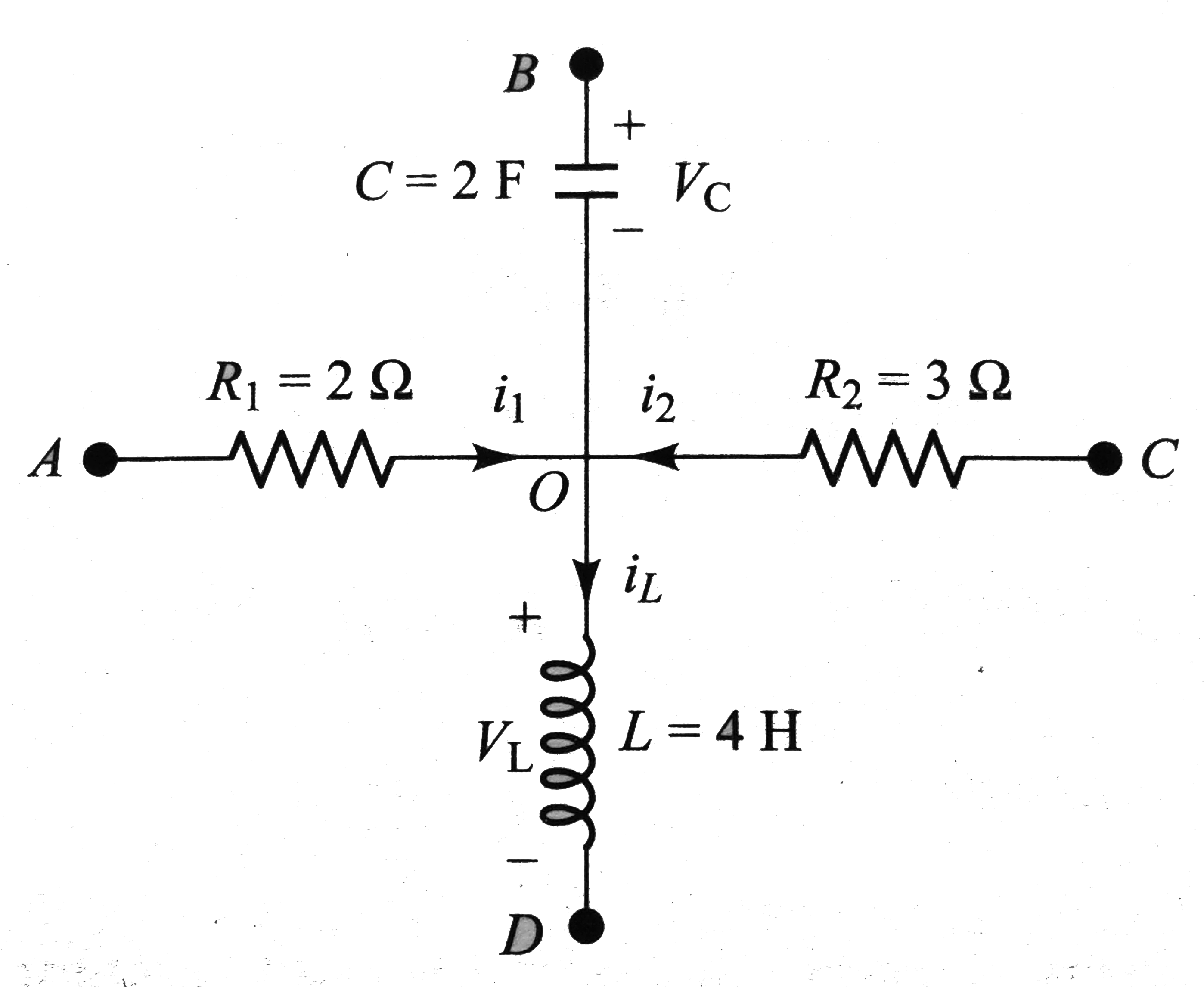
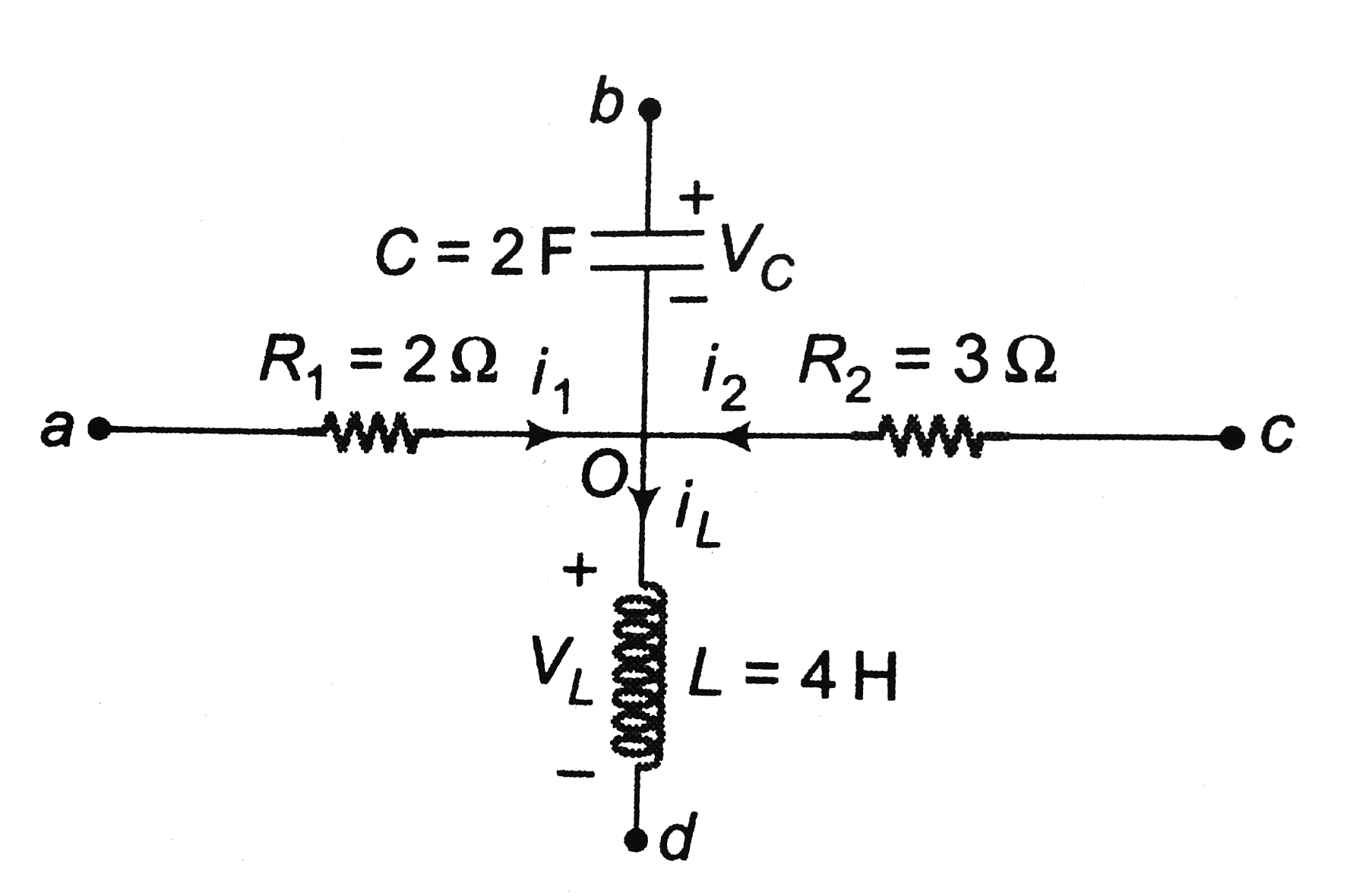In figure i1=10e−2tA,i2=4A,vC=3e−2tV
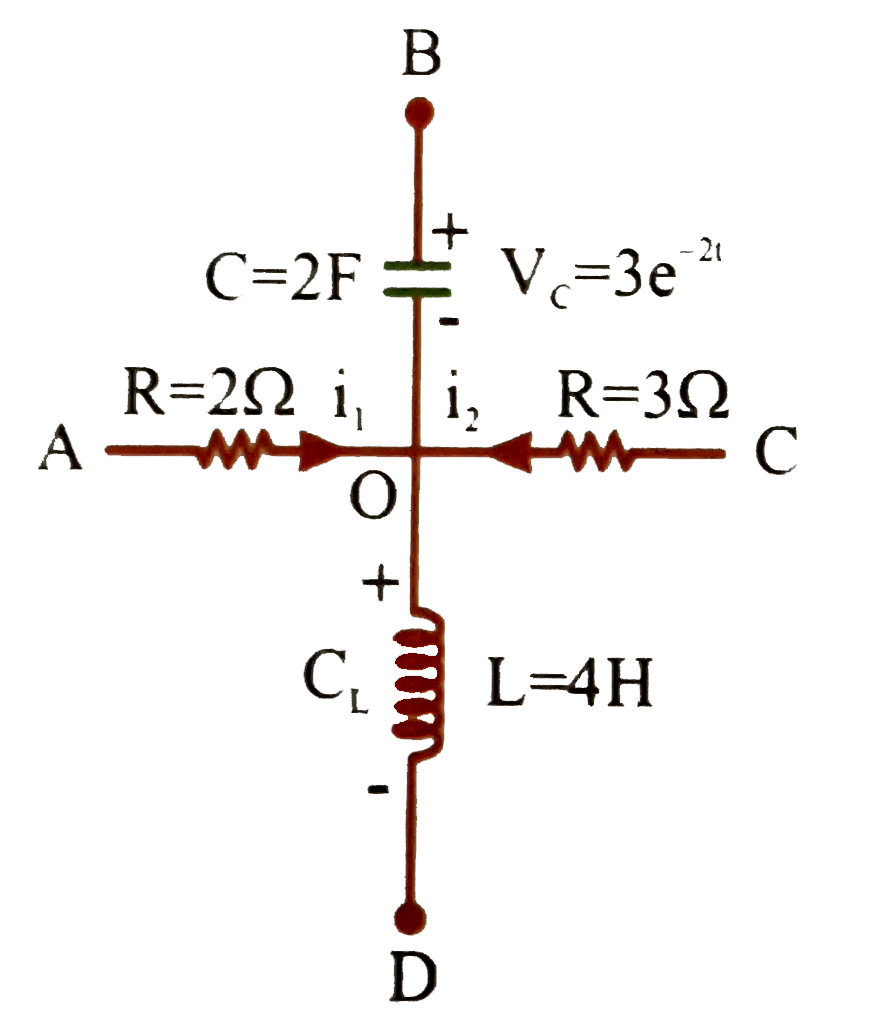
The current iL is
A
[2−2(1−e−2t)]A
B
[2+2(1−e−2t)]A
C
[3−2(1−e−2t)]A
D
[2+3(1−e−2t)]A
Video Solution
Text Solution
The correct Answer is:B
In current in the capacitor,
q=CVC=(2)(3e−2t)=6e−2tA
Current, ic=dqdt=−12e−2tA
Current flows from B to O.
From KVL, we have iL=i1+i2+ic
10e−2t+4−12e−2t=(4−2e−2t)A
=[2+2(1−e−2t)]A
|
Topper's Solved these Questions
- ALTERNATING CURRENTBook:NARAYNAChapter:ALTERNATING CURRENTExercise:LEVEL - VI
Explore 120 Videos
- ALTERNATING CURRENTBook:NARAYNAChapter:ALTERNATING CURRENTExercise:LEVEL - I (H.W)
Explore 23 Videos
- ALTERNATING CURRENTBook:NARAYNAChapter:ALTERNATING CURRENTExercise:LEVEL - IV NCERT Based Questions
Explore 15 Videos
- ATOMIC PHYSICSBook:NARAYNAChapter:ATOMIC PHYSICSExercise:LEVEL-II (H.W)
Explore 14 Videos
Similar Questions
Knowledge Check
In figure i1=10e−2tA,i2=4A,vC=3e−2tV
The variaton of current in the inductor with time can be repesented as :A B
B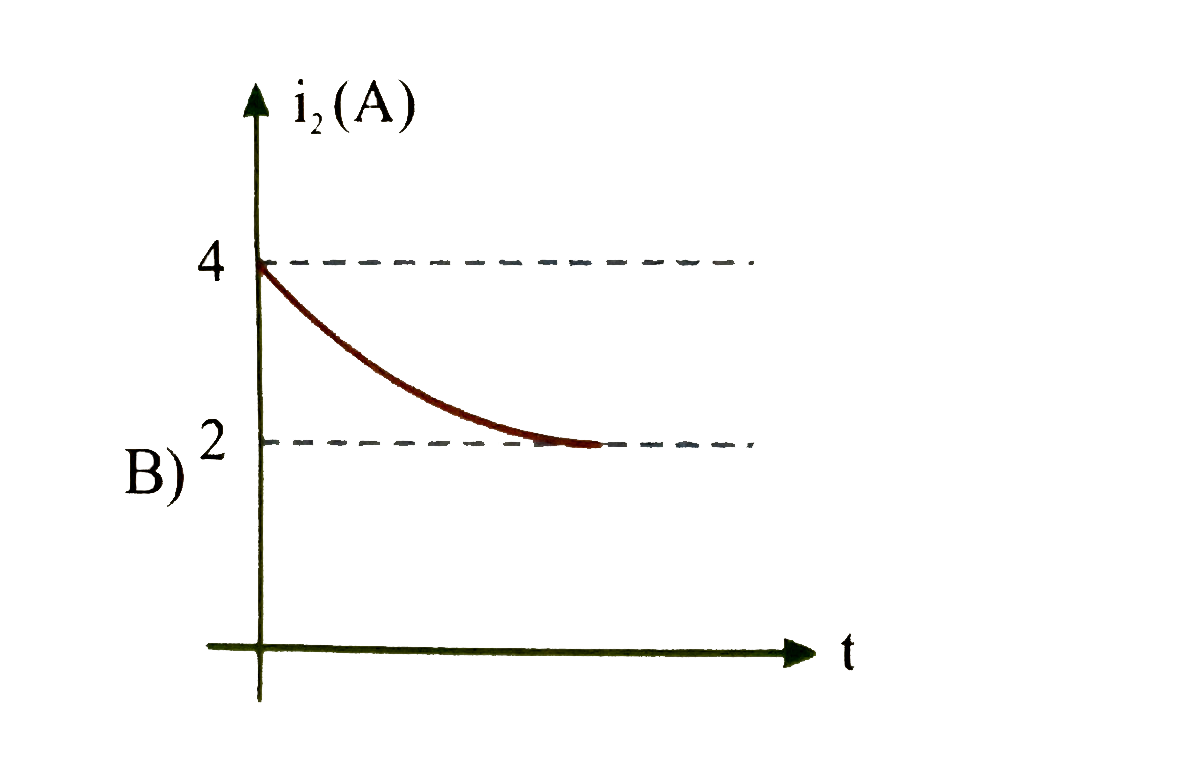 C
C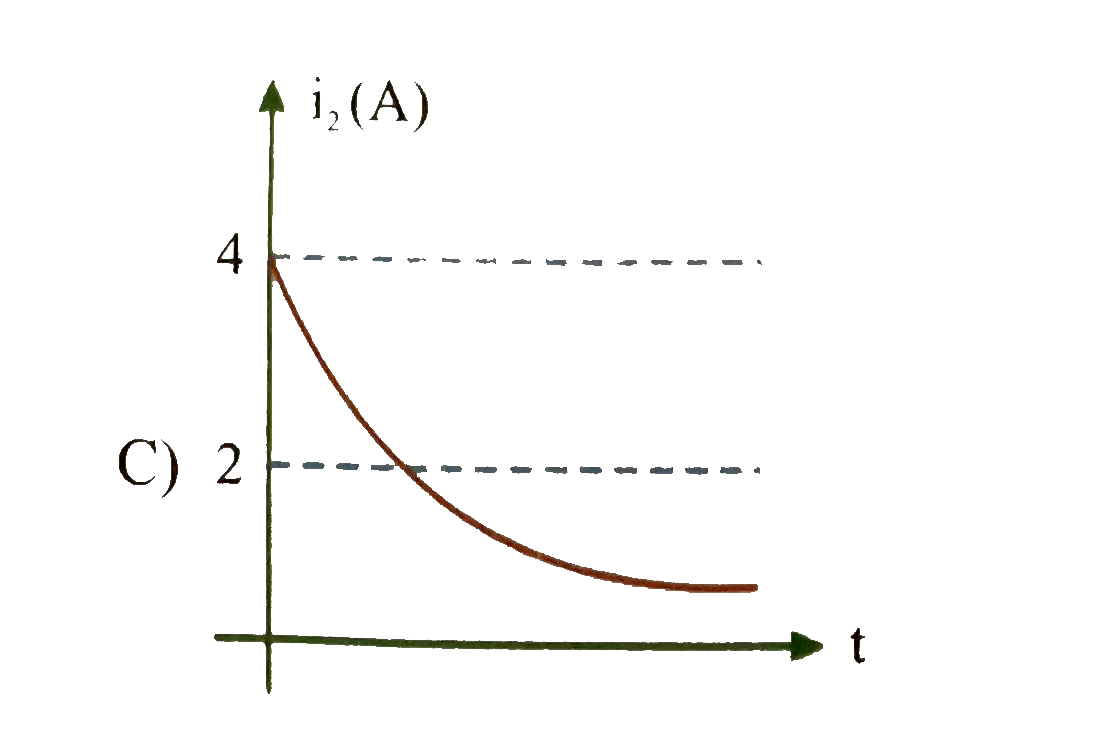 D
D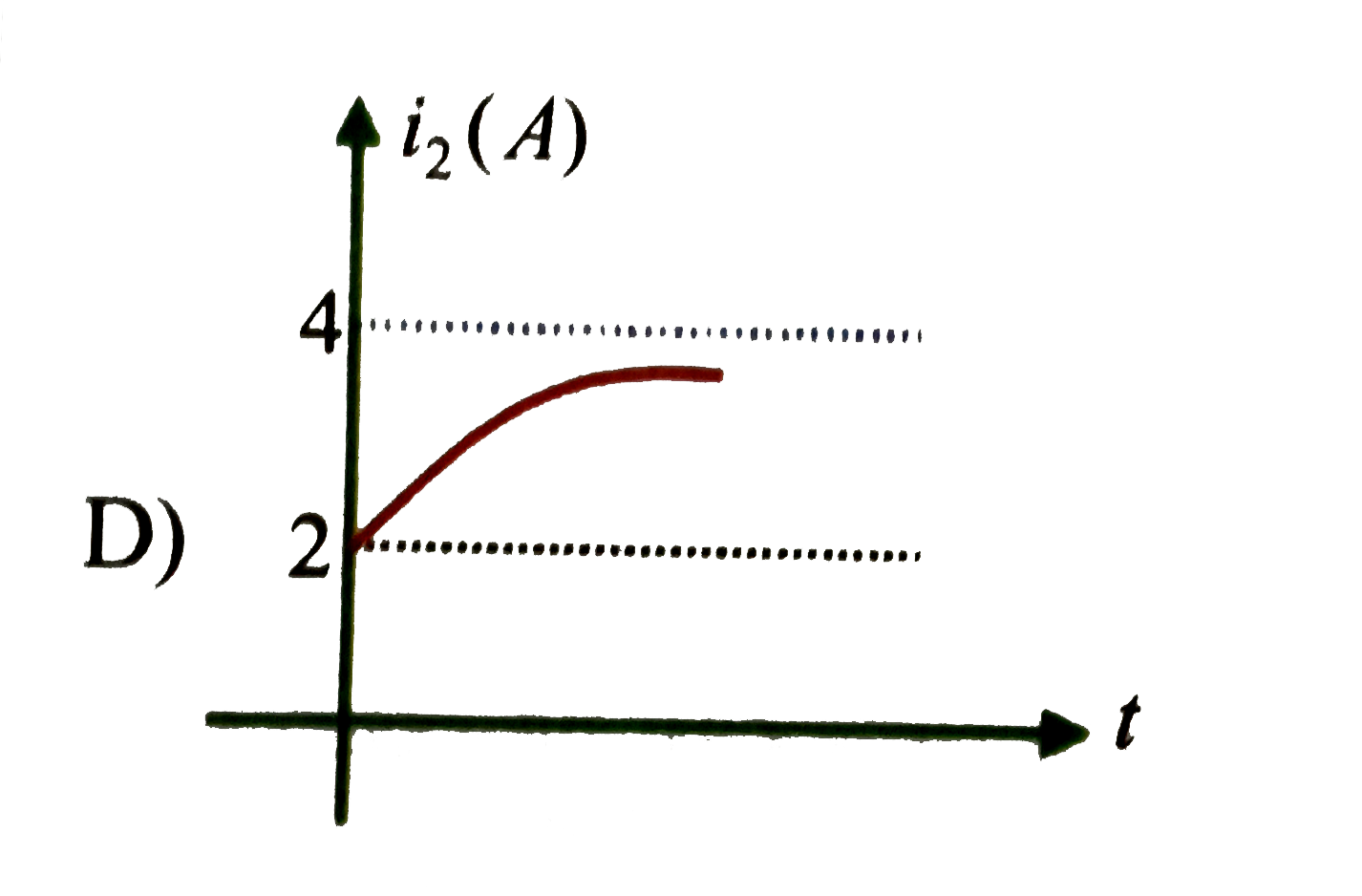
In figure i1=10e−2tA,i2=4A,vC=3e−2tV
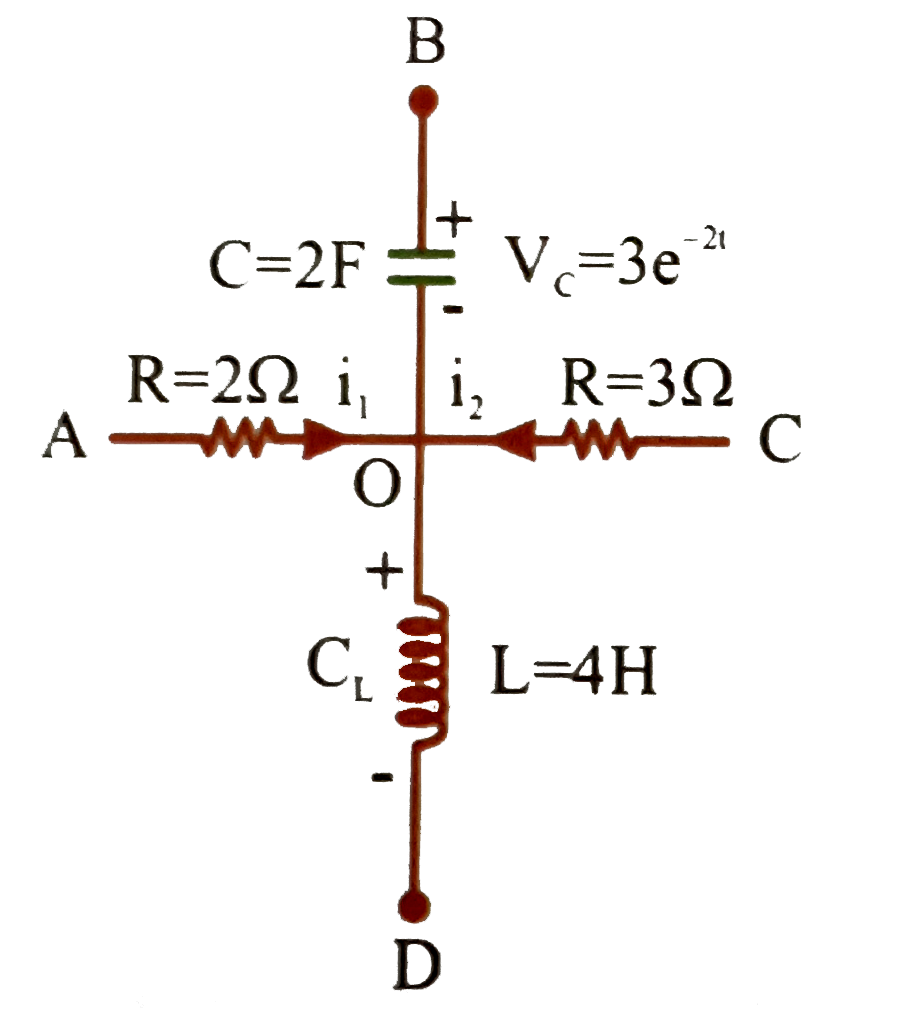
The potential difference across inductor VL is :A8e−2tVB9e−2tVC16e−2tVD18e−2tVIn figure i1=10e−2tA,i2=4A,vC=3e−2tV
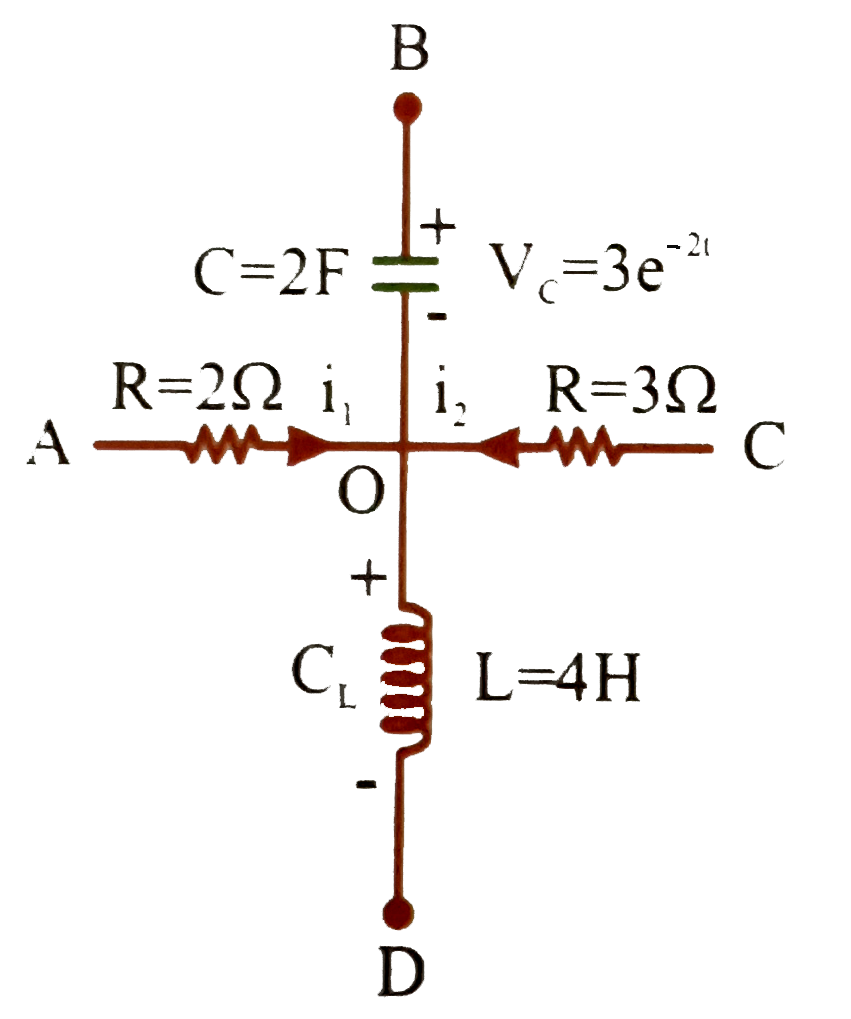
The potential difference across AB(VAB) is:A8e−2tVB12e−3tVC17e−2tD16e−2tV
In figure i1=10e−2tA,i2=4A,vC=3e−2tV
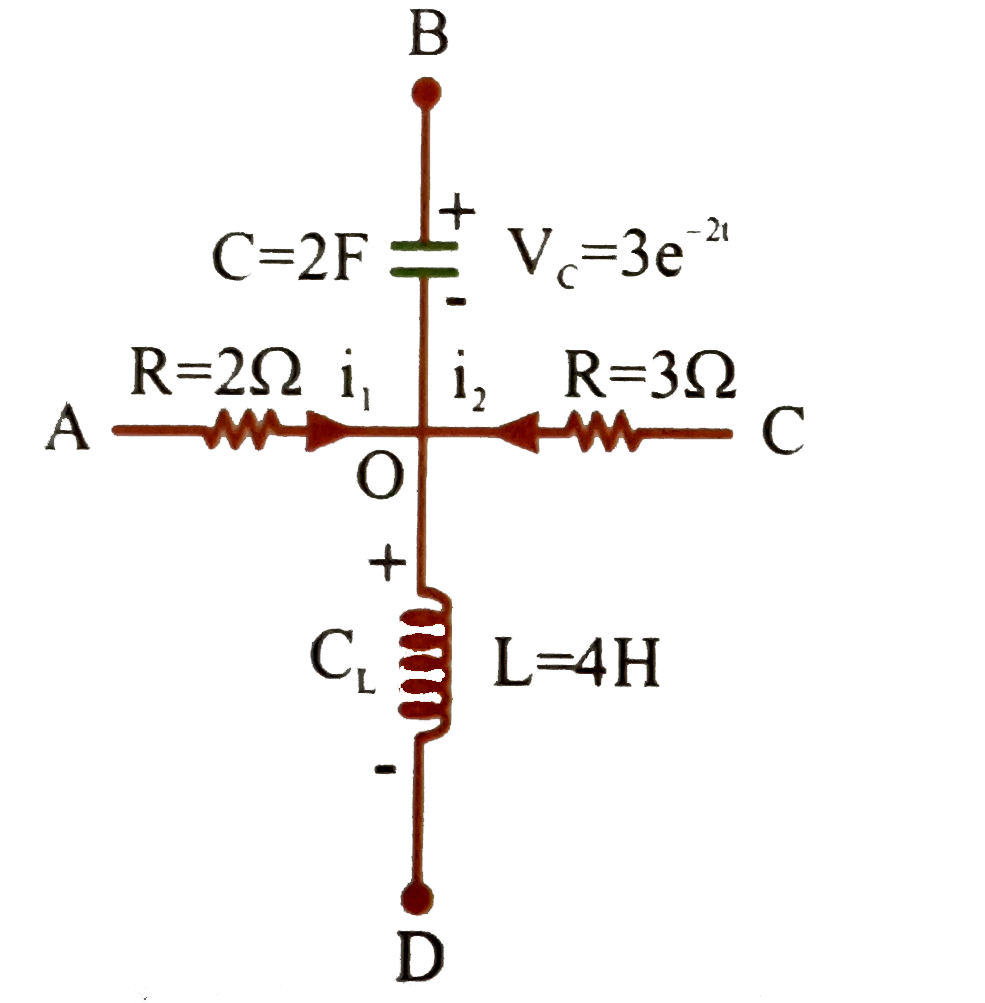
The variation of potential difference acorss A and C with time can be represented as
View SolutionIn Fig i1=10e−2tA, i2=4A, and VC=3e−2tV.
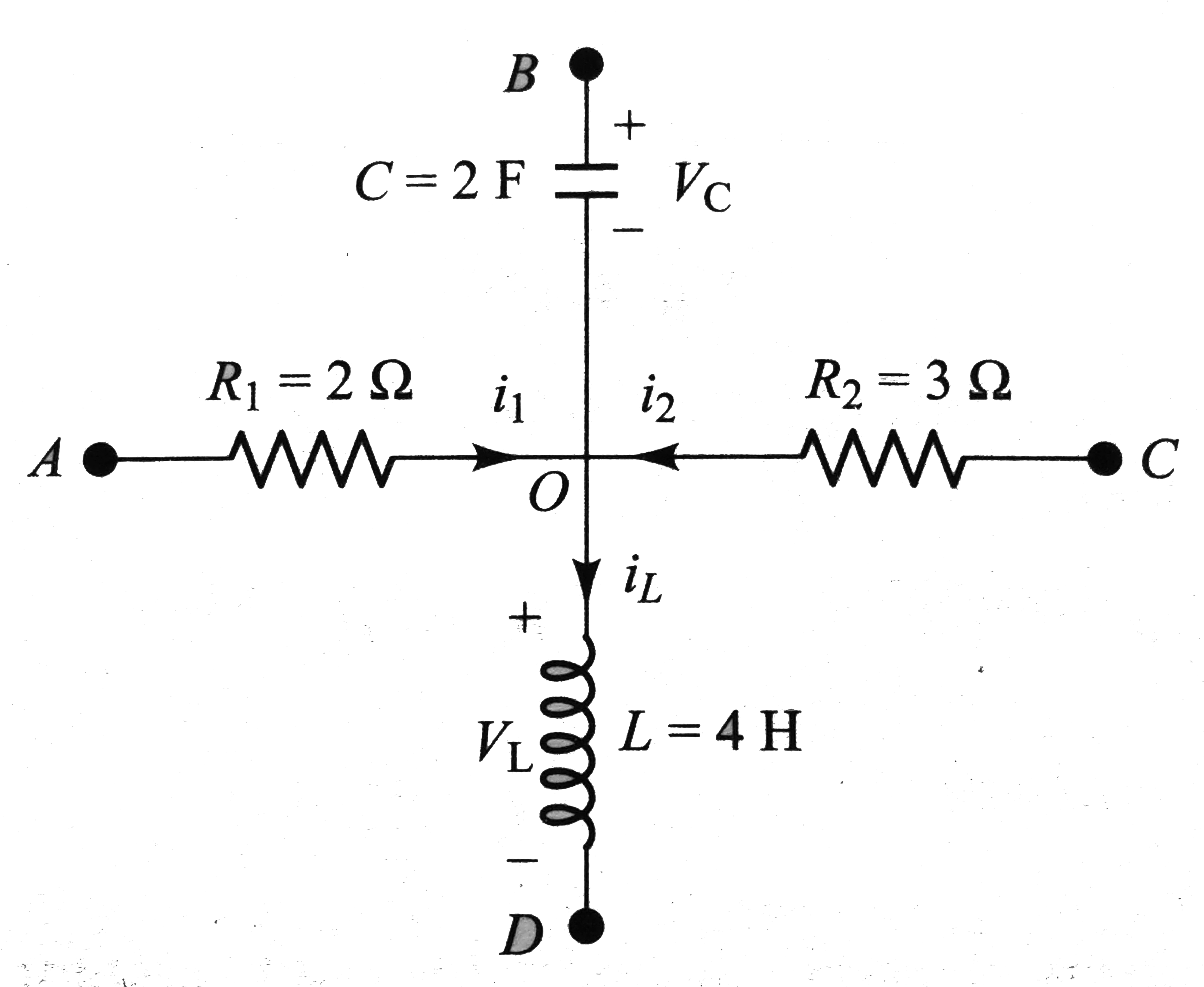
The variation of current in the inductor with time can be represented as
View SolutionIn Fig i1=10e−2tA, i2=4A, and VC=3e−2tV.
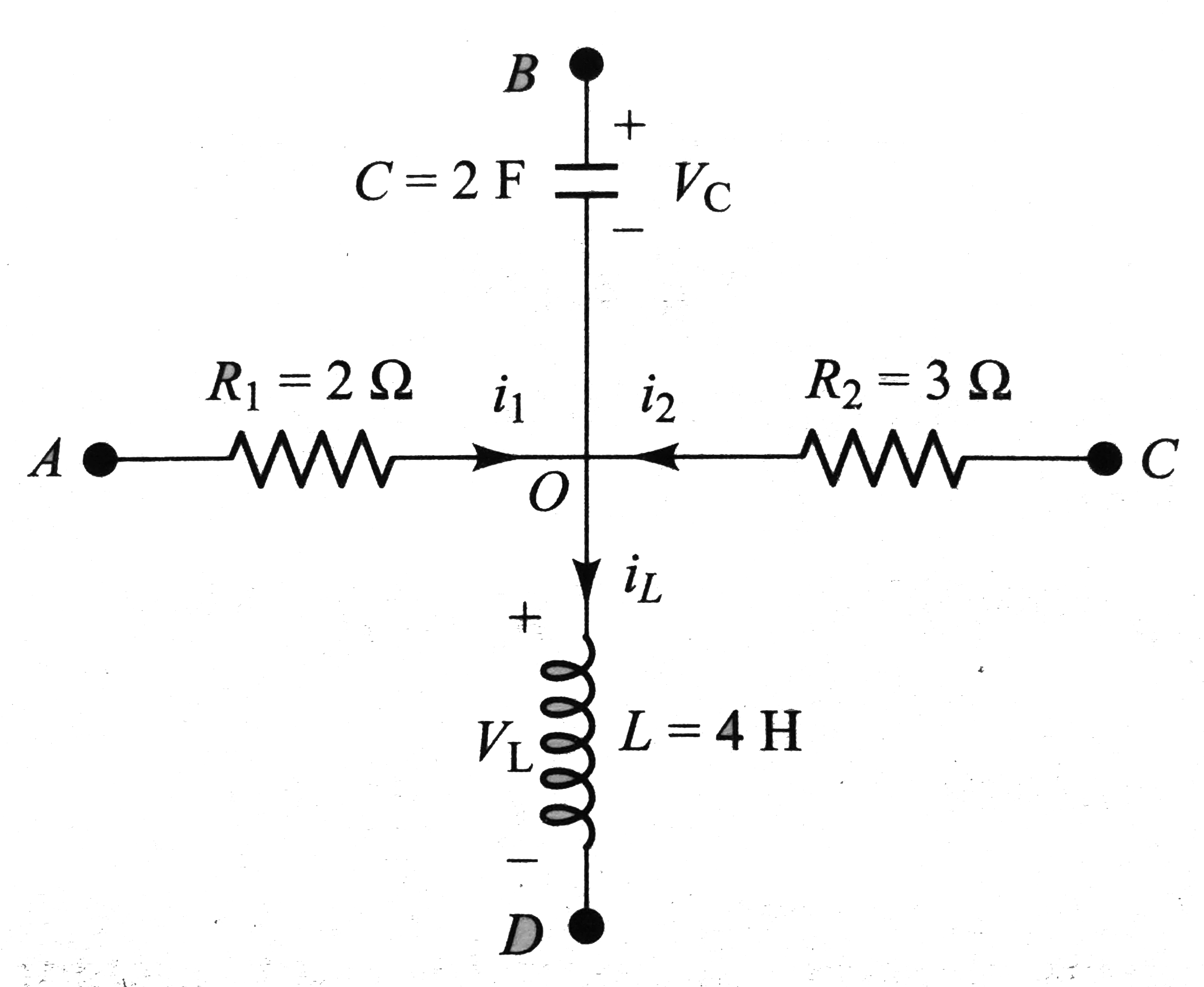
The variation of potential difference across C and D(VCD) with time can be expressed as
View SolutionIn Fig i1=10e−2tA, i2=4A, and VC=3e−2tV.
the vartiation of potential difference across A and C(VAC) with time can be respresented as
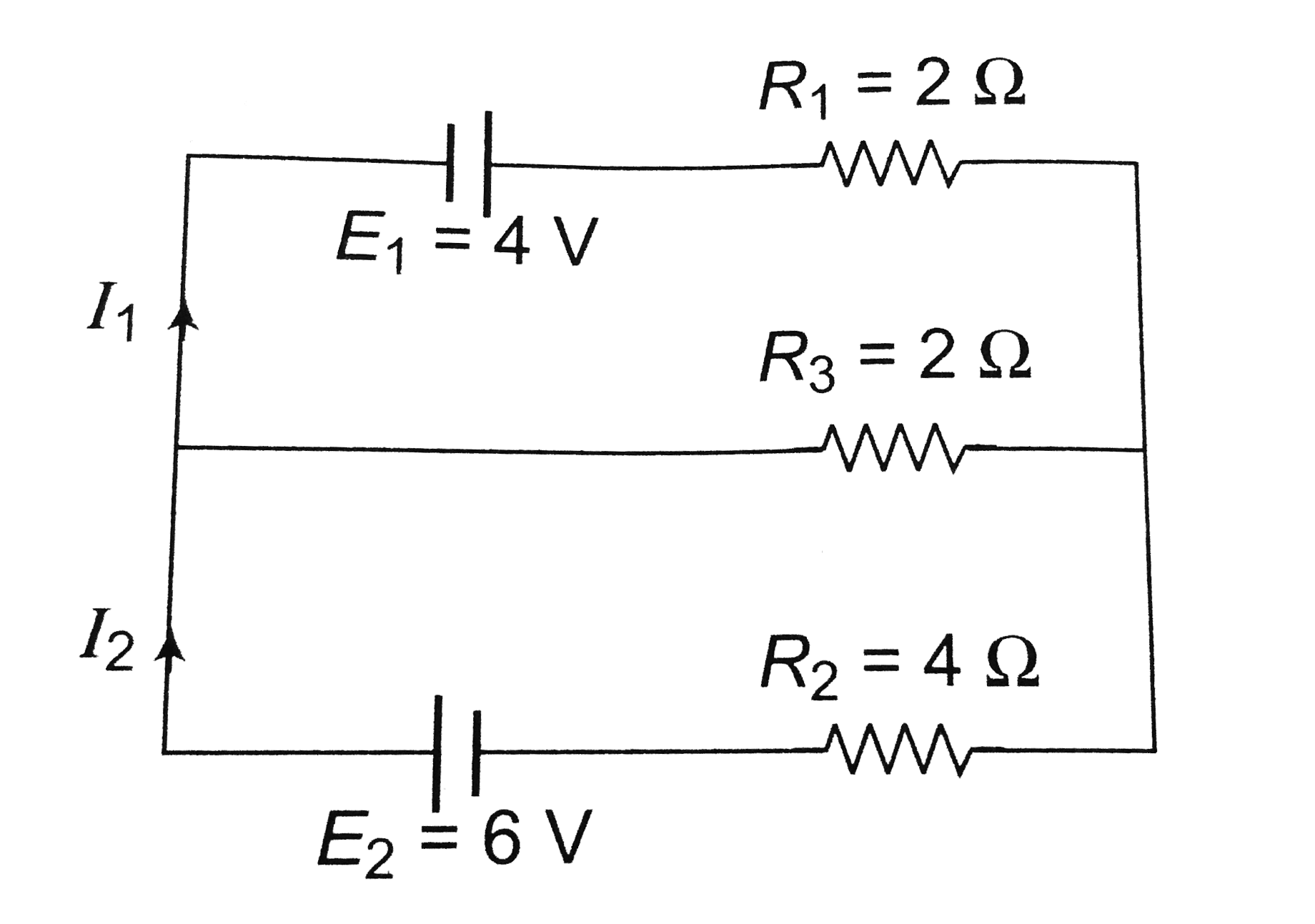
View SolutionIn the circuit shown below E1=4.0V,R1=2Ω,E2=6.0V,R2=4Ω and R3=2Ω. The current I1 is
View Solution