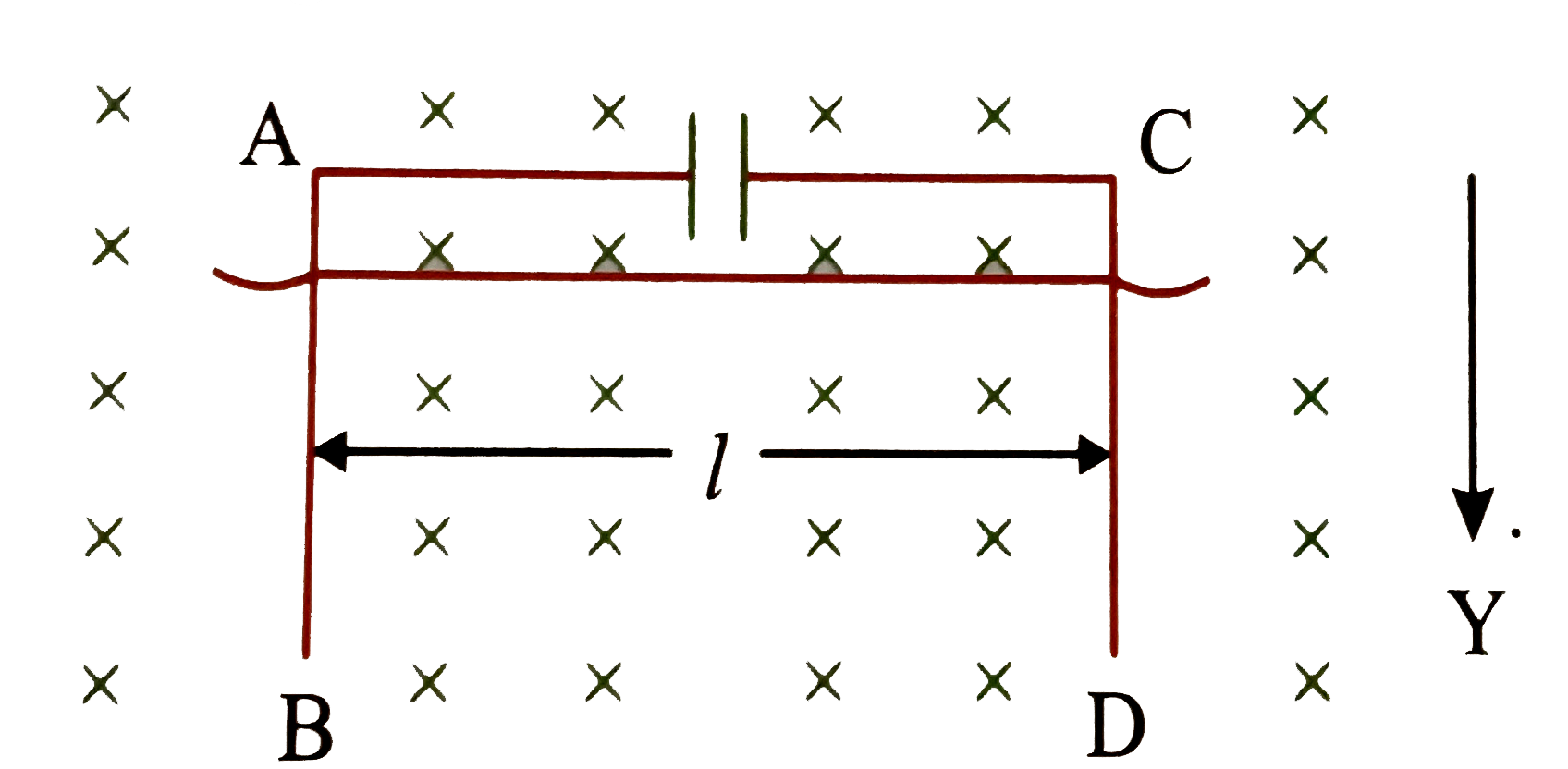
A conductor of mass m and length l is sliding smoothly an two vertical conducting rails AB and CD as shown in figure. The top ends of two conducting rails are joined by a capacitor of capacitance C. The conductor is relased from rest when it is very close to AC i.e., y=0. A uniform magnetic field B0 perpendicular to plane of figure existing. Neglect the resistance of rails and connecting wires. Take acceleration due to gravity to be g.

Based on above information answer the following questions:
Charge on the capacitor as a function of distance travelled y is given by
CB0l√2mgym+CB20l2
CB0l√m+CB20l22mgy
CB0lemgym+CB20l2
CB0l√2mgym+CB20l2×emgym+CB20l2
The correct Answer is:A
Let us say that in time t the conductor falls down by y and acquires a velocity v, then at this instant induced emf is
e=B0vl [with Q at higher potential]
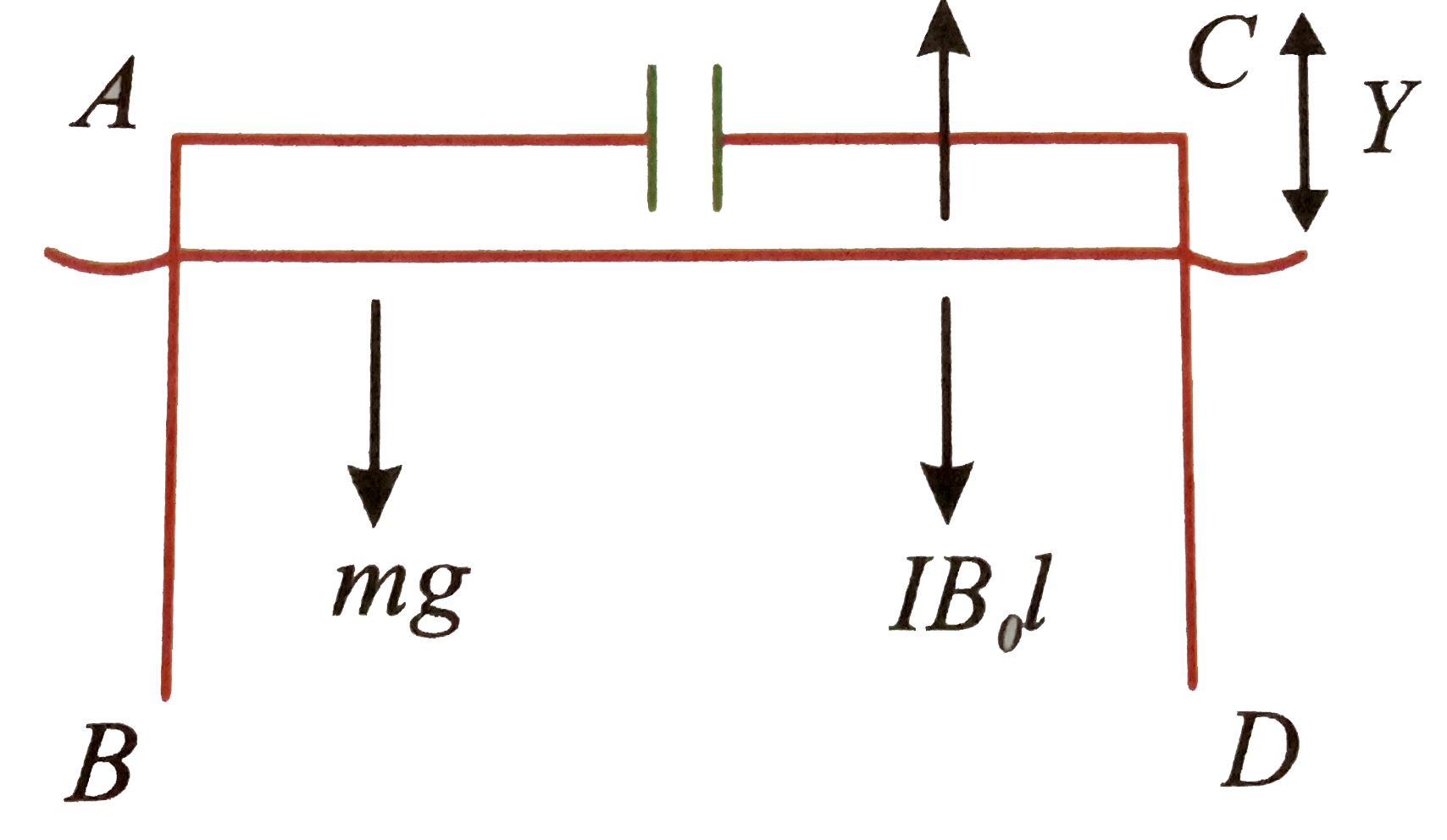
Charge on the capacitor at this instant is,
q=Ce=B0Cl×v
the current in the circuit at this instant is,
I=dqdt=B0Cldvdt=B0Cl×a
where a is the acceleration of the conductor at this instant.
Writing Newton's 2nd law equation for conductor,
mg−IB0l=ma
⇒a=mgm+CB20l2,
v=mgtm+CB20l2 and y=mgt22(m+CB20l2)
After solving above equations, we could have q as a function of y
E=r2dBdtdBdt=B0⇒E=a2B0

dτ=dF.a=(dqE).aτ∫dτ=Ea∫dq=Eaq
τ=Iα α=τI=Eaq(ma2)=Eqma
α=Eqma anticlockwise
P=τ.w=(Eaq)(αt)=EaqEqmat
Topper's Solved these Questions
- ELECTRO MAGNETIC INDUCTIONBook:NARAYNAChapter:ELECTRO MAGNETIC INDUCTIONExercise:Single Answer Questions Level -VI
Explore 13 Videos
- ELECTRO MAGNETIC INDUCTIONBook:NARAYNAChapter:ELECTRO MAGNETIC INDUCTIONExercise:Integer type questions
Explore 2 Videos
- ELECTRO MAGNETIC INDUCTIONBook:NARAYNAChapter:ELECTRO MAGNETIC INDUCTIONExercise:Single Answer Questions Level -V
Explore 11 Videos
- ELECTRIC CHARGES AND FIELDSBook:NARAYNAChapter:ELECTRIC CHARGES AND FIELDSExercise:EXERCISE -4
Explore 43 Videos
- ELECTRO MAGNETIC WAVESBook:NARAYNAChapter:ELECTRO MAGNETIC WAVESExercise:LEVEL-II(H.W)
Explore 14 Videos
Similar Questions
A conducting wire XY of mass M and negligible resistance slides smothly on two parallel conducting wires as shown in figure. The closed circuit has a resistance R due to AC. AB and CD are perfect conductors. There is a magnetic field B=B(t)ˆk
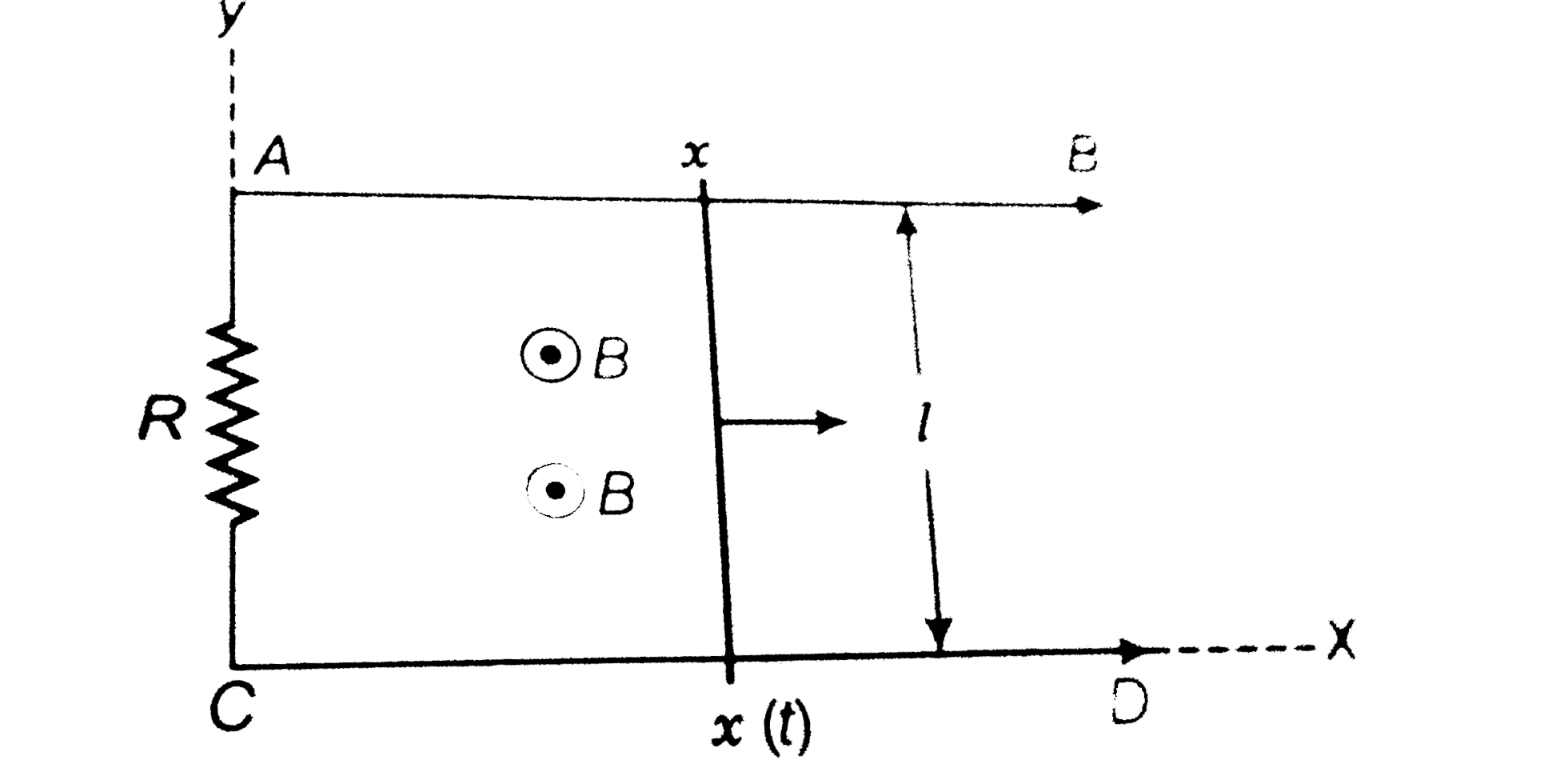
View SolutionA uniform rod AB of mass m and length l is placed over two smooth conducting rails P and Q. If the witch shown as closed at t=0, find the velocity of rod AB as a function of time.
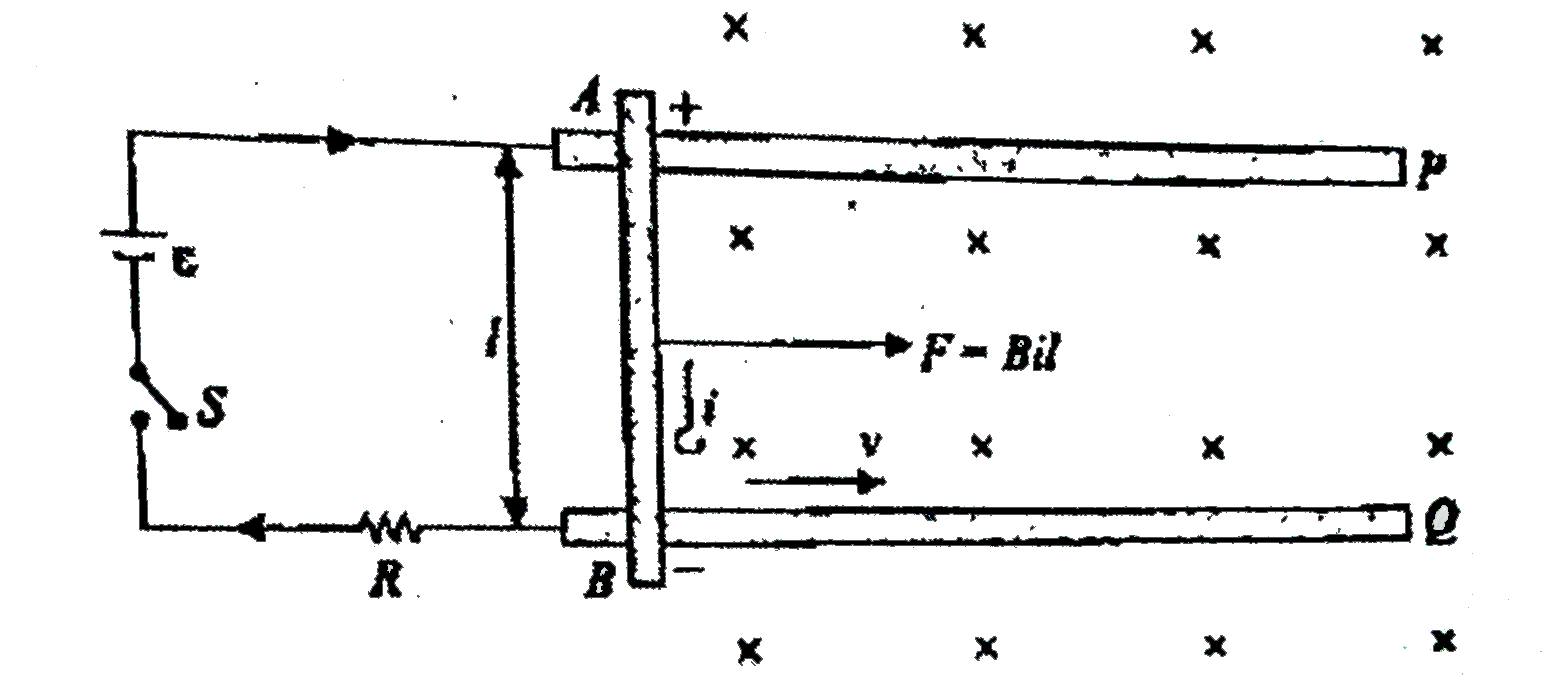
View Solution
Knowledge Check
A conductor of mass m and length l is sliding smoothly an two vertical conducting rails AB and CD as shown in figure. The top ends of two conducting rails are joined by a capacitor of capacitance C. The conductor is relased from rest when it is very close to AC i.e., y=0. A uniform magnetic field B0 perpendicular to plane of figure existing. Neglect the resistance of rails and connecting wires. Take acceleration due to gravity to be g.
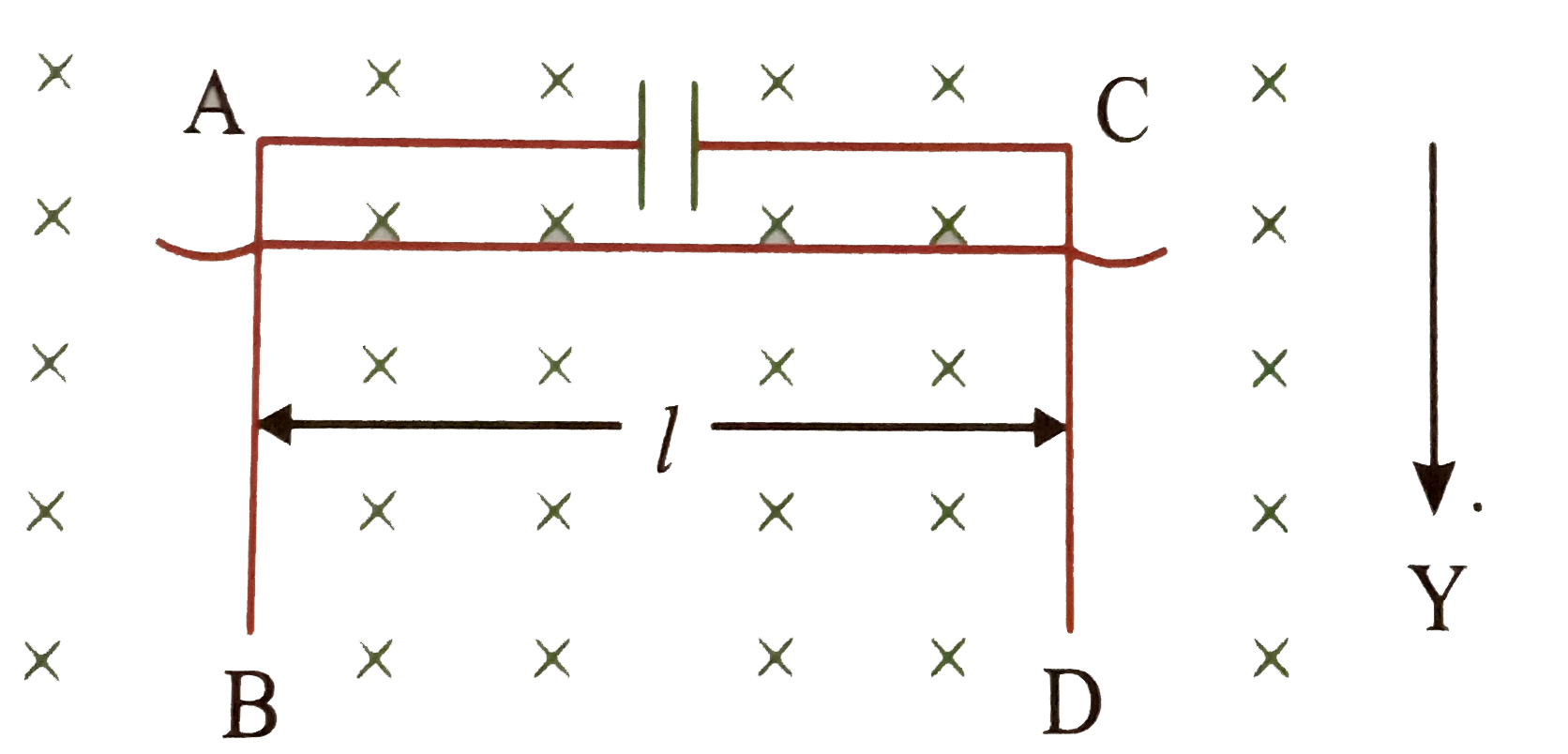
Based on above information answer the following questions:
Current in the circuit isAconstantBincreasing with timeCdecreasing with timeDFirst increase, then reaches a maximum value, and then starts decreasing to attain a constant value finallyA conductor of mass m and length l is sliding smoothly an two vertical conducting rails AB and CD as shown in figure. The top ends of two conducting rails are joined by a capacitor of capacitance C. The conductor is relased from rest when it is very close to AC i.e., y=0. A uniform magnetic field B0 perpendicular to plane of figure existing. Neglect the resistance of rails and connecting wires. Take acceleration due to gravity to be g.
Based on above information answer the following questions:
Mark the correct statement about the motion of conductorAIt is falling down with constant acceleration gBIt is falling down with constant acceleration but not equal to gCIt is falling down with increasing accelerationDIt is falling down with decreasing acceleration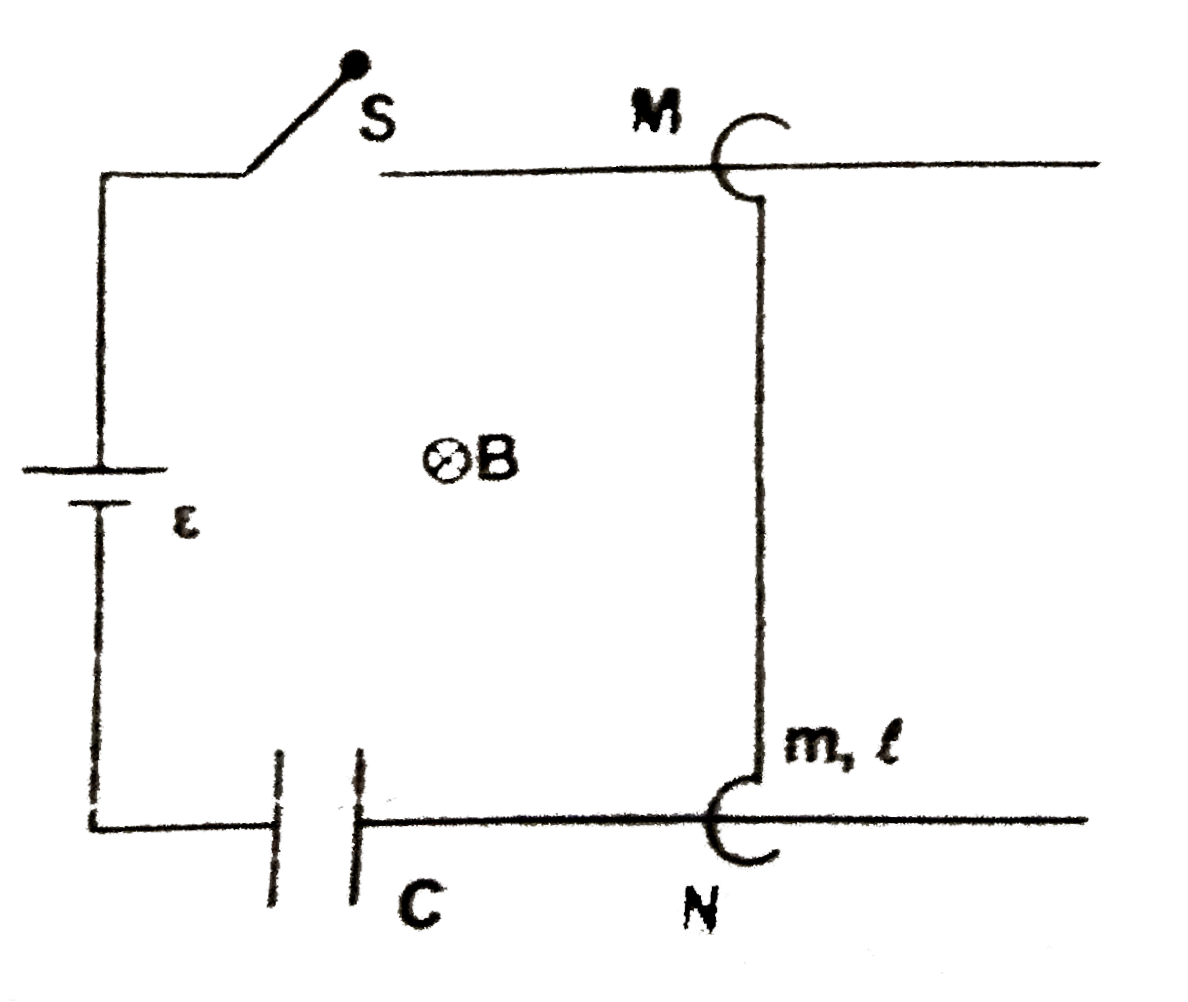
A conducting rod MN of mass m and length 'l' is placed on parallel smooth conducting rails connected to an uncharged capacitor of capacitance C and a battery of emf ε as shown. A uniform magnetic field B is existing perpendicular to the plane of the rails. The steady state velocity acquired by the conducting rod MN after closing switch S is (neglect the resistance of the parallel rails and the conducting rod)A2CBlε(m+CB2l2)BCBlε(m+CB2l2)CCBlε2(m+CB2l2)DCBlε4(m+CB2l2)
A straight horizontal conductor PQ of length l, and mass_ m slides down on two smooth conducting fixed parallel rails, set inclined at an angle 9 to the horizontal as shown in figure-5.30.
 The top end of the bar are connected with a capacitor of capacitance C. The system is placed in a uniform magnetic field, in the direction perpendicular to the inclined plane formed by the rails as shown in figure. If the resistance of the bars and the sliding conductor are negligible calculate the acceleration of sliding conductor as a function of time ifit is released from rest at t= 0
The top end of the bar are connected with a capacitor of capacitance C. The system is placed in a uniform magnetic field, in the direction perpendicular to the inclined plane formed by the rails as shown in figure. If the resistance of the bars and the sliding conductor are negligible calculate the acceleration of sliding conductor as a function of time ifit is released from rest at t= 0
View SolutionA conducting rod of length L=0.1m is moving with a uniform sped v=0.2m/s on conducting raisli a magnetic field B=0.5T as shown. On one side, the end of the rails is connected to a capacitor of capacitance C=20μF. Then, the charge on the capacitor's plates are

View SolutionA conducting wire xy of lentgh l and mass m is sliding without friction on vertical conduction rails ab and cd as shown in figure. A uniform magnetic field B exists perpendicular to the plane of the rails, x moves with a constant velocity of

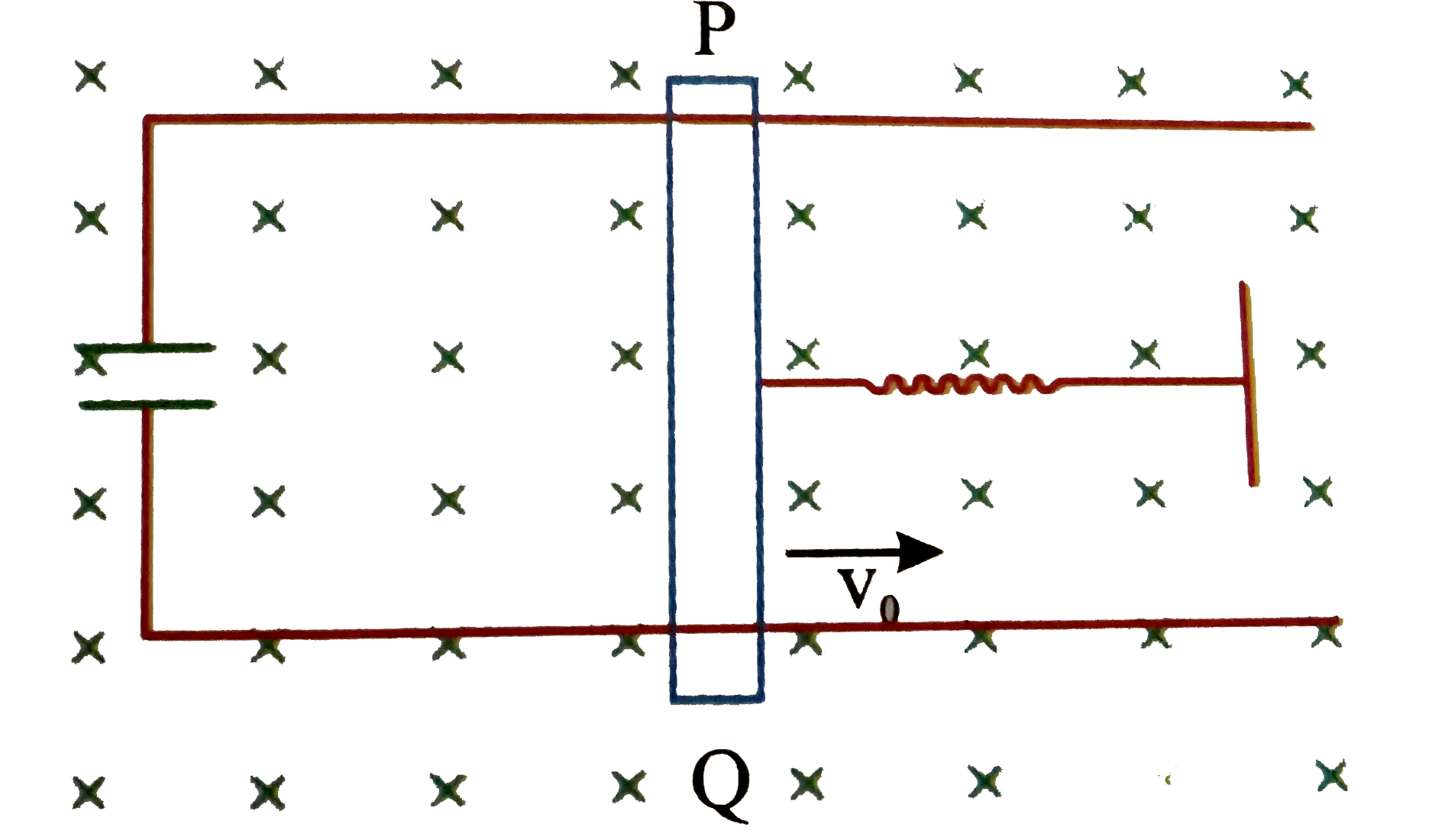
View SolutionA conducting rod PQ of mass m and length l is placed on two long parallel (smooth and conducting) rails connected to a capacitor as shown. The rod PQ is connected to a non conducting spring of spring constant k, which is initially in relaxed state. The entire arrangement is placed in a magnetic feild perpendicular to the plane of figure.
Neglect the resistance of the rails and rod.
Now, the rod is imparted a velocity v0 towards right, then acceleration of the rod as a function of its displacement x given by
View SolutionA uniform wire of mass m and length I can freely slide on a pair of parallel, frictionless, horizontal rails placed in a vertical constant magnetic field B (as shown in figure ). The rails are connected by a capacitor of capacitance C. The electric resistance of the circuit is zero. A constant horizontal force F acts on the middle point of wire begining t = 0 ,and the wire is at rest t = 0.
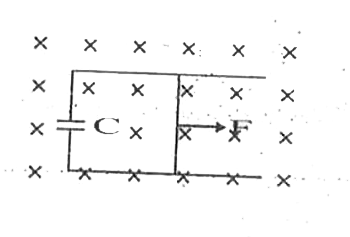
At t= 0 , acceleration of wire is
View Solution

