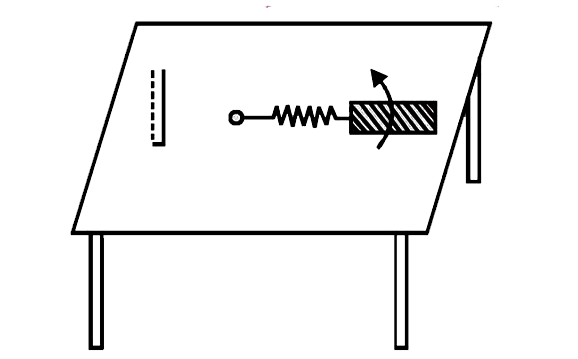
A metallic rod of length 'l' is tied to a string of length 2l and made to rotate with angular speed w on a horizontal table with one end of the string fixed. If there is a vertical magnetic field 'B' in the region, the e.m.f. Induced across the ends of the rod is

A

$\frac{3 B ω l^{2}}{2}$

B

$\frac{4 B ω l^{2}}{2}$

C

$\frac{5 B ω l^{2}}{2}$

D

$\frac{2 B ω l^{2}}{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

As rod is rotating in magnetic field thus cutting magnetic field lines, motional emf will develop a cross the rod. As each and every element of the rod is moving with different velocity. For calculating emf across rod we first consider an element of length $d x$ at a distance $x$ from the fixed end of the string

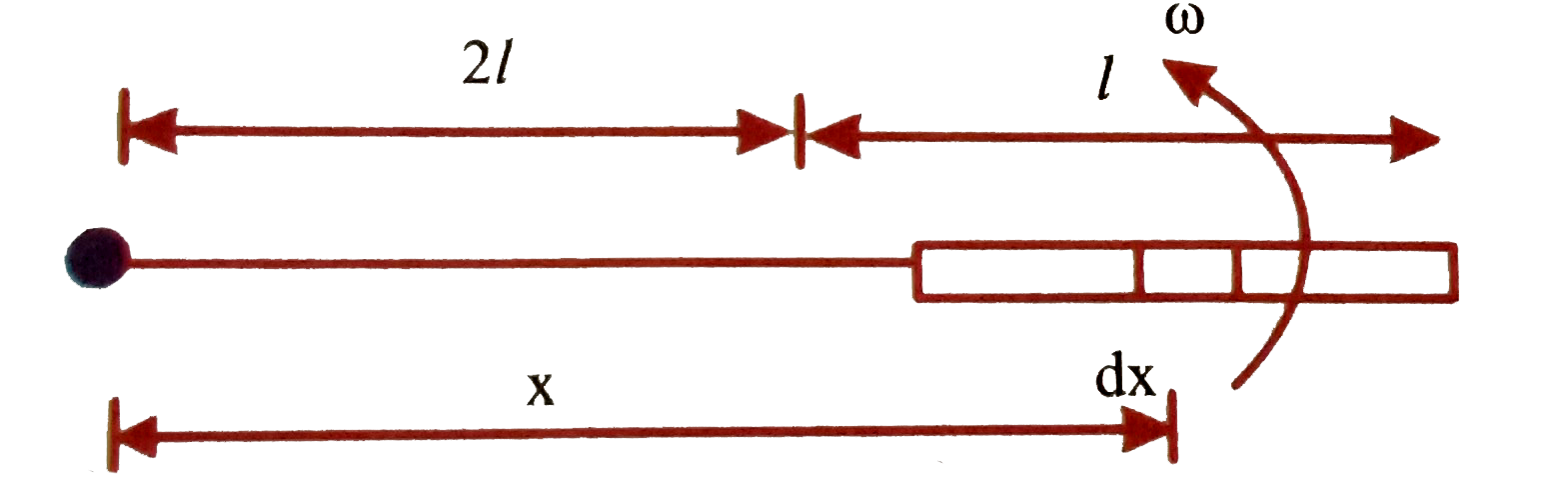
e.m.f induced in the element is
$d ε = b (ω x) d x$
Hence, the e.m.f. induced across the ends of the rod is
$ε = 3 l \int 2 l B ω x d x = B ω {[\frac{x^{2}}{2}]}_{2 l}^{3 l} = \frac{B ω}{2} [{(3 l)}^{2} - {(2 l)}^{2}]$
$= \frac{5 B ω l^{2}}{2}$

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTROMAGNETIC INDUCTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A conducting rod of length $2 l$ is rotating with constant angular speed $w$ about its perpendicular bisector. A uniform magnetic field $B$ exists parallel to the axis of rotation. The e.m.f. induced between two ends of the rod is

A $B ω l^{2}$
B $\frac{1}{2} B ω l^{2}$
C $\frac{1}{8} B ω l^{2}$
Dzero
Question 2 - Select One
A sphere of mass m is tied to end of a string of length l and rotated through the other end along a horizontal circular path with speed v . The work done in full horizontal circle is
A0
B $(\frac{m v^{2}}{l}) .2 π l$
C $m g .2 π l$
D $(\frac{m v^{2}}{l}) . (l)$
Question 3 - Select One
A conducting rod of length 2l is rotating with constant angular speed $ω$ about is perpendicular bisector. A uniform magnetic field $\to B$ exists parallel to the axis of rotation. The e.m.f. induced between two ends of the rod is

A $\frac{1}{2} B ω l^{2}$
B $\frac{1}{8} B ω l^{2}$
CZero
D $B ω l^{2}$

NARAYNA-ELECTRO MAGNETIC INDUCTION-Level - III

Home
Ask Doubt
Profile