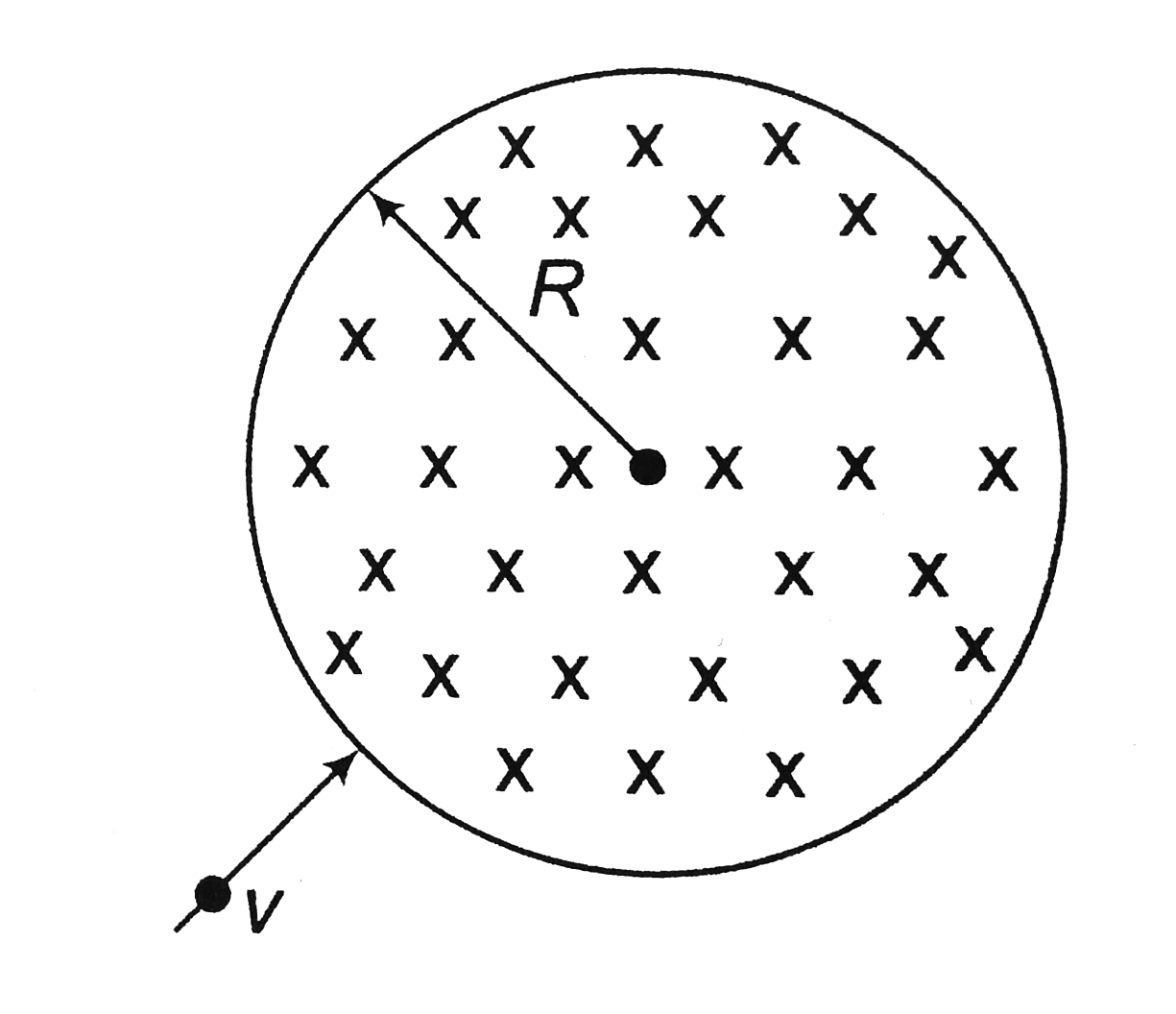
A particle of mass m having a charge q enters into a circular region of radius R with velocity v directed towards the centre. The strength of magnetic field is B. Find the deviation in the path of the particle.
The correct Answer is:(a)B0=μ0i0a22πC(b2−a2) (d)B=0
(a) On the axis of rod due to i1→B is zero on axis
i2=jπa2 and j=iπ(b2−a2)
Due to infinite wire we know that B=μ0i2πd
Hence due to i2 at the axis of rod
B0=μ0i22πC=μ0(jπa2)2πC=μ0iπ(b2−a2)πa12πC
B0=μ0i2a22πC(b2−a2)B0=μ0ia22πC(b2−a2)
Similarly we can find on the axis of hole

(b)j=iπ(b2−a2),∫Bdl=μ0iin,
B2πC=μ01π(b2_a2)πC2,B=μ0iC2π(b2−a2)
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBook:NARAYNAChapter:MOVING CHARGES AND MAGNETISMExercise:LEVEL-VI (SINGLE ANSWER QUESTION)
Explore 81 Videos
- MOVING CHARGES AND MAGNETISMBook:NARAYNAChapter:MOVING CHARGES AND MAGNETISMExercise:Level =I (H.W)
Explore 42 Videos
- MOVING CHARGES AND MAGNETISMBook:NARAYNAChapter:MOVING CHARGES AND MAGNETISMExercise:NCERT Based Questions
Explore 20 Videos
- MAGNETISM AND MATTERBook:NARAYNAChapter:MAGNETISM AND MATTERExercise:EXERCISE - 4 (SINGLE ANSWER TYPE QUESTION)
Explore 17 Videos
- NUCLEAR PHYSICSBook:NARAYNAChapter:NUCLEAR PHYSICSExercise:LEVEL-II-(H.W)
Explore 9 Videos
Similar Questions
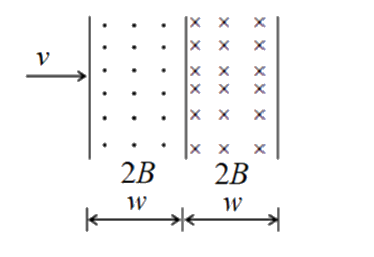
The figure shows two regions of uniform magnetic field of strengths 2B and 2B. A charged particle of mass m and charge q enters the region of the magnetic field with a velocity υ=qBwm, where w is the width of each region of the magnetic field. The time taken by the particle to come out of the region of the magnetic field is
View SolutionA positive charge particle of charge q, mass m enters into a uniform magnetic field with velocity v as shown in the figure. There is no magnetic field to the left of PQ. Find
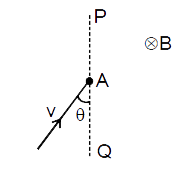
time spent
View Solution
Knowledge Check
A particle of mass m and charge q enters a magnetic field B perpendicularly with a velocity v, The radius of the circular path described by it will be
ABq/mvBmq/BvCmB/qvDmv/BqA charged particle of mass m and charge q describes circular motion of radius r in a uniform magnetic field of strength B. The frequency of revolution is
A3Bq2πmB3Bq2πmC2πm2BqDBq2πmA charged particle of mass m is moving with a speed u in a circle of radius r. If the magnetic field induction at the centre is B, the charge on the particle is
A4πr2Bμ0uB2πr2Bμ0uCmuBrD2muBr
A charged particle of mass m and charge q is accelerated through a potential difference of V volts. It enters a region of uniform magnetic field which is directed perpendicular to the direction of motion of the particle. Find the radius of circular path moved by the particle in magnetic field.
View SolutionA particle of mass M and charge Q moving with velocity v describes a circular path of radius R when subjected to a uniform transverse magnetic field of induction B. The work done by the field when the particle completes one full circle is :
View SolutionIf the velocity of the charged particle is doubled and strength of magnetic field is halved, then radius becomes
View SolutionA charged particle of mass m and charge q enters a magnetic field B with a velocity v at an angle θ with the direction of B. The radius fo the resulting path is
View SolutionA particle of mass m and charge q enters a region of magnetic field (as shown) with speed v at t = 0. There is a region in which the magnetic field is absent as shown. The particle after entering the region collide elastically with a rigid wall. Time t after which the velocity of particle become antiparallel to its initial velocity is -

View Solution

