If the work required to move the conductor shown in figure, one full turn in the positive direction at a rotational frequency N revolutions per minute, if →B=B0ˆar(B0 is positive constant and ˆar is a unit vector in radial direciton ), is yπrB0il. Then y is .

The correct Answer is:2
The magnetic force on the conductor is
→FB=I→L×→B=ILˆk×B0ˆar=B0IL(ˆaϕ)
External force is
→Fext=B0IL(−ˆaϕ)
Where ˆaϕ is a unit vector in tangential direction. Therefore work done requuired to turn the conductor in one full revolution is :
W=∫2π0B0IL(−ˆaϕ).rdϕˆaϕ=−2πrB0IL
The negative sign shows that field work. The fact that work is down around a closed path shows that the force is non− conservative in this case.
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBook:NARAYNAChapter:MOVING CHARGES AND MAGNETISMExercise:LEVEL-VI (SINGLE ANSWER QUESTION)
Explore 81 Videos
- MOVING CHARGES AND MAGNETISMBook:NARAYNAChapter:MOVING CHARGES AND MAGNETISMExercise:Level =I (H.W)
Explore 42 Videos
- MOVING CHARGES AND MAGNETISMBook:NARAYNAChapter:MOVING CHARGES AND MAGNETISMExercise:NCERT Based Questions
Explore 20 Videos
- MAGNETISM AND MATTERBook:NARAYNAChapter:MAGNETISM AND MATTERExercise:EXERCISE - 4 (SINGLE ANSWER TYPE QUESTION)
Explore 17 Videos
- NUCLEAR PHYSICSBook:NARAYNAChapter:NUCLEAR PHYSICSExercise:LEVEL-II-(H.W)
Explore 9 Videos
Similar Questions
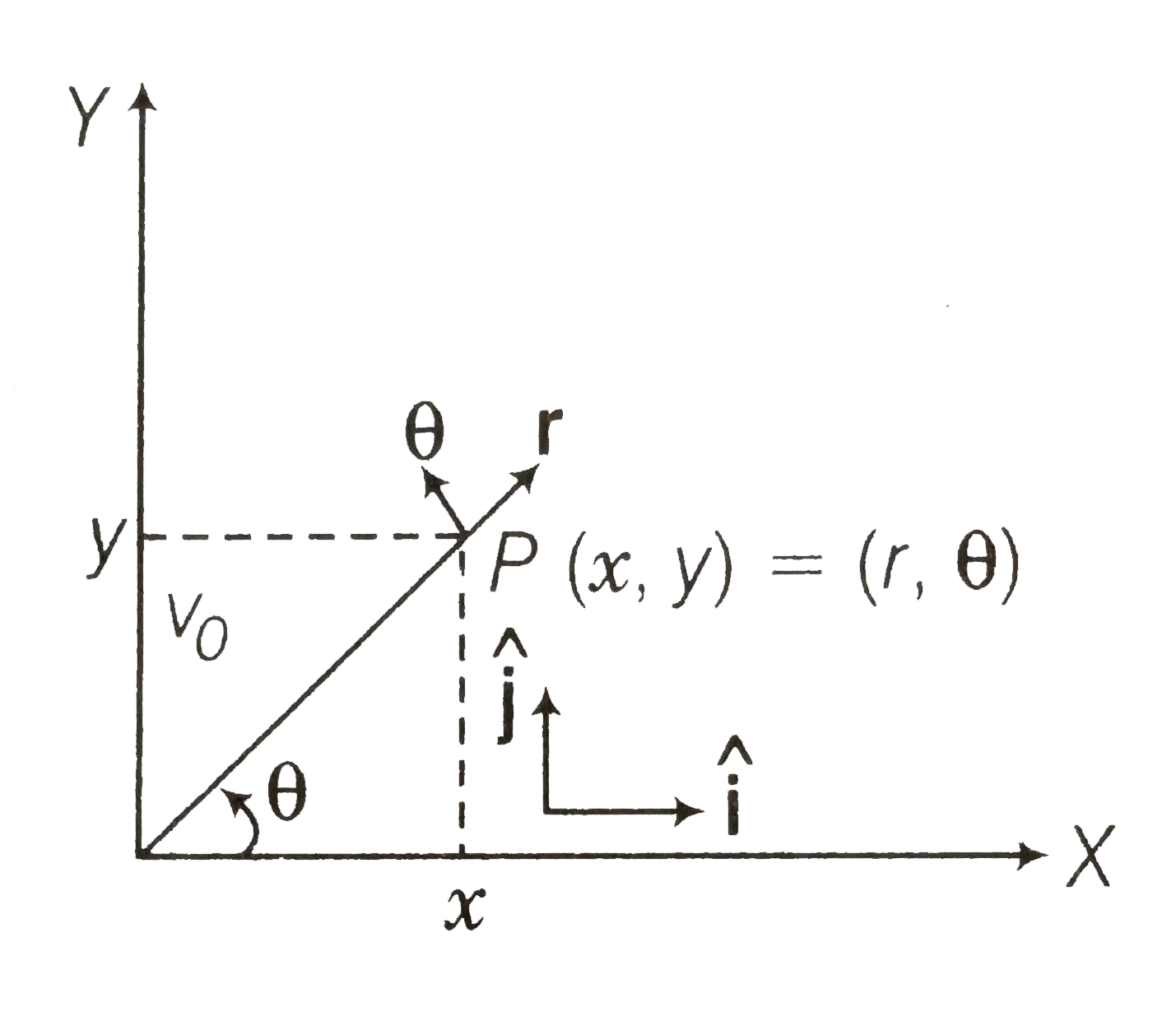
Motion in two dimensions, in a plane can be studied by expressing position, velocity and acceleration as vectors in cartesian coordinates A=Axˆi+Ayˆj, where ˆi and ˆj are unit vector along x and y-directions, respectively and Ax and Ay are corresponding components of A. Motion can also be studied by expressing vectors in circular polar coordinates as A=Arˆr+Aθˆθ, where ˆr=rr=cosθˆi+sinθˆj and ˆθ=−sinθˆi+cosθˆj are unit vectors along direction in which r and θ are increasing.
(a) Express ˆi and ˆj in terms of ˆr and ˆθ.
(b) Show that both ˆr and ˆθ are unit vectors and are perpendicular to each other.
(c) Show that ddt(ˆr)=ωˆθ, where ω=dθdt and ddt(ˆθ)=−θˆr.
(d) For a particle moving along a spiral given by r=aθˆr, where a = 1 (unit), find dimensions of a .
(e) Find velocity and acceleration in polar vector representation for particle moving along spiral described in (d) above.
View SolutionA vector vec Awhenadded→the→−−→r vec B = 3. 0 hat i+ 4 hat jyieldsarestant–––––→−−→rtˆis∈thepositivey−directionandhasamagn∫udeequal→tˆof vec B.F∈dthemagnitudeof vec A .
View Solution
Knowledge Check
Find the work and power required to move the conductor of length l shown in the fig. one full turn in the anticlockwise direction at a rotational frequency of n revolutions per second if the magnetic field is of magnitude B0 everywhere and points radially outwards from Z-axis. The figure shows that surface traced by the wire AB.
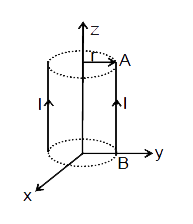 A−2πrB0il,−2πrB0ilnB4πrB0il,4πrB0ilnC2πrB0il,2πrB0ilnD−4πrB0il,4πrB0iln
A−2πrB0il,−2πrB0ilnB4πrB0il,4πrB0ilnC2πrB0il,2πrB0ilnD−4πrB0il,4πrB0ilnFigure shows sqare current caarrying coil of edge lengthL. The magnetic field on the coil is given by →B=B0yLˆi+B0xLˆj where B0 is a positive constant.
 AIf coil is free to rotate about x axis torque on the coil is given by 12iAB0ˆiBIf coil is free to rotate about y-axis torque on coil is given by −12iAB0ˆjCResultant force on coil is zero.DEquation for the torque →μ×→B where mu is magnetic moment of coil is not valid on the coil.
AIf coil is free to rotate about x axis torque on the coil is given by 12iAB0ˆiBIf coil is free to rotate about y-axis torque on coil is given by −12iAB0ˆjCResultant force on coil is zero.DEquation for the torque →μ×→B where mu is magnetic moment of coil is not valid on the coil.In a region at a distance r from z-axis, magnetic field →B=B0rtˆk is present where B0 is constant and t is time. Then the magnetic of induced electric field at a distance r from z-axis is given by
Ar2B0Br22B0Cr23B0Dnone
A magnetic field →B=B0ˆj , exists in the region a<x<2a , and vec(B) = -B_(0) hat(j),∈theregion2a lt xlt 3a,whereB_(0)isapositiveconstant.Apositivep∮char≥mov∈gwithavelocityvec(v) = v_(0) hat (i),wherev_(0) is a positive constant , enters the magnetic field at x=a . The trajectory of the charge in this region can be like

View SolutionIf →a=4ˆi−ˆj,→b=−3ˆi+2ˆjand→c=−ˆk. Then the unit vector ˆr along the direction of sum of these vectors will be
View SolutionA particle is moving with a position vector, →r=[a0sin(2πt)ˆi+a0cos(2πt)ˆj]. Then -
View SolutionA vector →A When added to the vector →B=3ˆi+4ˆj yields a resultant vector that is in the positive y-direction and has a magnitude equal to that of →B. Find the magnitude of →A.
View SolutionA magnetic field →B=B0ˆj exists in the region a<x<2a and →B=−B0ˆi in the region 2a<x<3a, where B0 is positive constant. A positive point charge moving with a velocity →v=v0ˆi where v0 is a positive constant, enters.
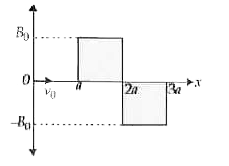
the magnetic field at x=a, The trajectory of the charge in this region can be like,
View Solution

