The magnetic field is confirmed in a square region. A positive charged particle of charge q and mass m the limiting velocities of the particles so that it may come out of face (1), (2), (3), and (4). 
For the positive charge coming out from face (1), the radius of the path in magnetic field should be less than or equal to l/4 . For limiting case

rmax=l4=mvqB⇒vmax=qBl4m. Hence, if the velocity is <qBl4m, the charge particle comes out of face (1). We can observe from right palm rule that the particle cannot come out from face (1). For a positive charge coming out of face (4) let particle come out at point N from ΔOMN
(ON)2=(OM)2+(MN)2,
r2=(r−12)2+t2⇒r=54l.If the particle comes out from face (4),r<54⇒mvqB<54l(or)v<54qBlm. If velocity v>54qBlm, the particle will come out from face 3.
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - NARAYNACHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - C.U.Q-KEY
121 Videos
- MOVING CHARGES AND MAGNETISMBOOK - NARAYNACHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - LEVEL-I(C.W)
58 Videos
- MAGNETISM AND MATTERBOOK - NARAYNACHAPTER - MAGNETISM AND MATTEREXERCISE - EXERCISE - 4 (SINGLE ANSWER TYPE QUESTION)
17 Videos
- NUCLEAR PHYSICSBOOK - NARAYNACHAPTER - NUCLEAR PHYSICSEXERCISE - LEVEL-II-(H.W)
9 Videos
Similar Questions
A charged particle of mass m1 and charge q1 is revolving in a circle of radius r .Another charged particle of charge q2 and mass m2 is situated at the centre of the circle.If the velocity and time period of the revolving particle be v and T respectively then
View SolutionA charged particle is moving with velocity Vin magnetic field
View Solution
Knowledge Check
A charged particle of charge Q and massm moves with velocity v in a circular path due to transverse magnetic field, B, then its frequency is
AQB2πmBQvB2πmCQmvB2πDvb2πQmA positively charged particle projected towards east is deflected towards north by a magnetic field. The field may be
Atowards westBtowards southCupwardDdownwardA charged particle of charge q and mass m enters perpendiculalry in a magnetic field B. Kinetic energy of particle E, then frequency of rotation is
AqBmπBqB2πmCqBE2πmDqB2πE
If the value of magnetic field is reduced to half and velocity of charged particle is doubled then the radius of path of charged particle will be:
View SolutionA charged particle enters into a uniform magnetic field with velocity v0 perpendicular to it , the length of magnetic field is x=√32R, where R is the radius of the circular path of the particle in the field .The magnitude of change in velocity of the particle when it comes out of the field is
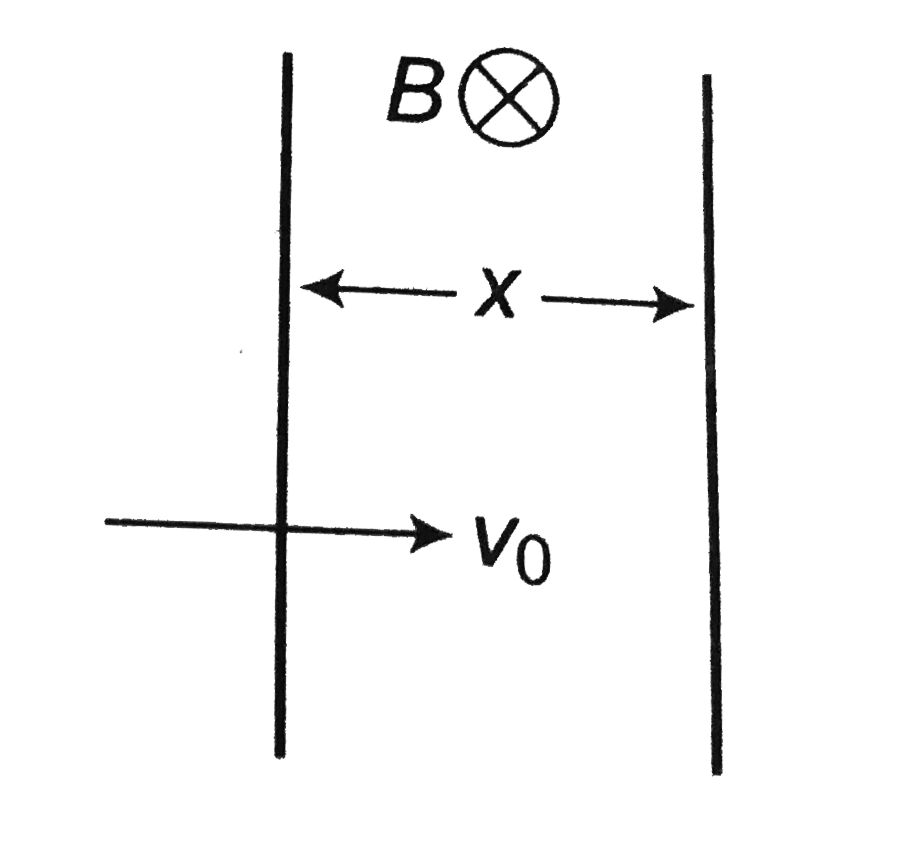
View SolutionIf a charged particle (+q) is projected with certain velocity parallel to the magnetic field, then it will
View SolutionIf a charged particle (+q) is projected with certain velocity parallel to the magnetic field , then it will
View Solutionthe magnetic field shown in the figure consist of the two magnetic fields.
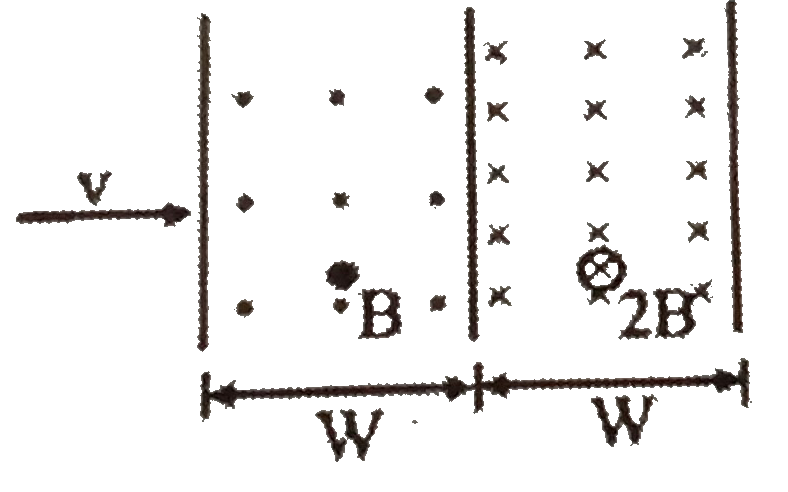
If v is the velocity just required for a charge particles of mass m and charge q to pass through the magnetic field. Particle is projected with velocity 'v' then how much time does such a charge spend in the magntic filed-
View Solution