A rectangular conducting loop consists of two wires on two opposite sides of length l joined together by rods of length d. The wires are each of the same material but with cross-sections differing by a factor of 2. The thicker wire has a resistance R and the rods are of low resistance, which in turn are connected to a constant voltage source V0. The loop is placed in a uniform magnetic field B at 45∘ to its plane. Find τ, the torque exerted by the magnetic field on the loop about an axis through the centres of rods.
V0AB4√2R
V0AB√2R
V0AB2√2R
3V0AB√2R
The correct Answer is:A
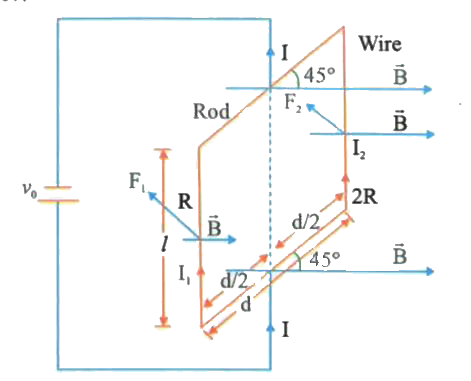
F1=I1lB,τ1=F1(d2)cos45∘=(I1lB)d2√2 and F2=I2lB,τ2=F2(d2)cos45∘
=(I2lB)d2√2
Since →F1 and →F2 are in the same direction net torque exerted by the magnetic field on the loop i.e.,
τ=τ1−τ2(I1−I2)lBd2√2
Since I1=V0R and I2=V02R
τ=(V0R−V02R)lBd2√2=V0AB4√2R
(∵Id=A) are of the loop
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - NARAYNACHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE - 3
29 Videos
- MAGNETISM AND MATTERBOOK - NARAYNACHAPTER - MAGNETISM AND MATTEREXERCISE - EXERCISE - 4 (SINGLE ANSWER TYPE QUESTION)
17 Videos
- NUCLEAR PHYSICSBOOK - NARAYNACHAPTER - NUCLEAR PHYSICSEXERCISE - LEVEL-II-(H.W)
9 Videos
Similar Questions
Two wires are of the same material but of different lengths and areas of cross-section. Will their resistivities be same or different ?
View SolutionTwo wires of the same metal have the same length, but their cross-sections are in the ratio of 3:1. They are joined in series. The resistance of the thicker wire is 10Ω. The total resistance of the combinations will be
View Solution
Knowledge Check
A rectangular conducting loop consists of two wires on two opposite sides of length l joined together by rods of length d. The wires are each of the same material but with cross-sections differing by a factor of 2. The thicker wire has a resistance R and the rods are of low resistance, which in turn are connected to a constant voltage source V0. The loop is placed in a uniform magnetic field B at 45∘ to its plane. Find τ, the torque exerted by the magnetic field on the loop about an axis through the centres of rods.
AV0AB4√2RBV0AB√2RCV0AB2√2RD3V0AB√2RTwo wire of the same meta have same length, but their cross-sections are in the rati 3:1 . They are joined in series. The resistance of thicker wire is 10Ω . The total resistance of the combination will be
A10ΩB20ΩC40ΩD100ΩTwo wires of the same metal have same length, but their cross-sections are in the ratio 3:1 . They are joined in series. The resistance of thicker wire is 10Ω. The total resistance of the combination will be
A2.5ΩB40/3ΩC40ΩD100Ω
Two wires of same metal have the same length but their cross- sections are in the ratio 1 :3 . They are joined in series. The resistance of the thicker wire is 10Ω . The total resistance of the combination will be
View SolutionA cylindrical conductor of length l and uniform area of cross-section A has resistance R. Another conductor of length 2l and resistance R of the same material has area of cross-section :
View SolutionA cylindrical conductor of length l and uniform area of cross section A has resistance R. Another conductor of length 2l and resistance R of the same material has an area of cross section
View SolutionTwo wires made of the same material and having the same volume are connected in series. Their cross sectional areas are in the ratio 1:3. If the thicker wire has a resistance of 20Ω, then the equivalent resistance of the series combination is
View SolutionA cylindrical conductor of length l and uniform area of cross section A has resistance R. Another conductor of length 2.5l and resistance 0.5R of the same material has an area of cross section
View Solution
