Two very small particles 1 and 2 each of mass 0.5kg and of charge q1=1mc and q2=1μC resepectivley are connected by a mass less spring of spring constant 200Nm−1 and placed on a horizontal rough surface.The particle 1 is fixed and 2 is free to move ,Initially the spring is in its natural length (2m) where q2 is released.If coefficient of static friction between 2 and horizontal surface is 0.5 the separation between the charges when they are in equilibrium will be (Neglect gravitational interactions between 1 and 2g=10ms−2
The correct Answer is:2
Based on friction and Coulombus Law
F=9×109×10−94=2.25N
which is less μmg acting on 2 rArr final separation =2m only.
Topper's Solved these Questions
- ELECTROSTATICS AND GAUSS LAWBook:NARAYNAChapter:ELECTROSTATICS AND GAUSS LAWExercise:ASSERTION AND REASON
Explore 10 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBook:NARAYNAChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCEExercise:ADDITIONAL PROBLEMS
Explore 14 Videos
- EXPERIMENTAL PHYSICSBook:NARAYNAChapter:EXPERIMENTAL PHYSICSExercise:Comprehension type
Explore 6 Videos
Similar Questions
Two blocks A and B of mass m and 2m respectively are connected by a light spring of force constant k. They are placed on a smooth horizontal surface. Spring is stretched by a length x and then released. Find the relative velocity of the blocks when the spring comes to its natural length

View SolutionTwo masses m1andm2 re connected by a spring of spring constnt k and are placed on as frictionless horizontal surface. Initially the spring is tretched through a distance x0 when the system is released from rest. Find the distance moved by the tow masses before they again come to rest.
View Solution
Knowledge Check
Two blocks of masses m1=1kg and m2 = 2kg are connected by a spring of spring constant k = 24 N/m and placed on a frictionless horizontal surface. The block m1 is imparted an initial velocity v0 = 12cm/s to the right. The amplitude of osciallation is
A2 cmB1 cmC3 cmD4 cmTwo blocks of masses m1 and m2 are connected by a massless spring and placed on smooth surface. The spring initially stretched and released. Then :
Athe momentum of each particle remains constant separatelyBthe magnitude of momentums of each body are equal to each otherCthe mechanical energy of system remains constantDboth (C) and (B) are correctTwo uniform discs A and B of equal radii but having different masses 1 kg and 2 kg respectively, are connected (at centres) by a massless spring of spring constant k=1000Nm−1 and then placed on a sufficiently rough horizontal surface. If initially, the system is released from rest with the spring being compressed by 10 cm, then the speed of A when the spring comes back to its natural length, is
 AvA=√409ms−1BvA=√209ms−1CvA=√203ms−1DvA=√403ms−1
AvA=√409ms−1BvA=√209ms−1CvA=√203ms−1DvA=√403ms−1
Two blocks m1andm2 are connected by a spring of force constant K and are placed on a frictionless horizontal surface. Initially the spring is given extension x0 when the sysetem is released from rest, find the distance moved by two blocks before they again comes to rest.
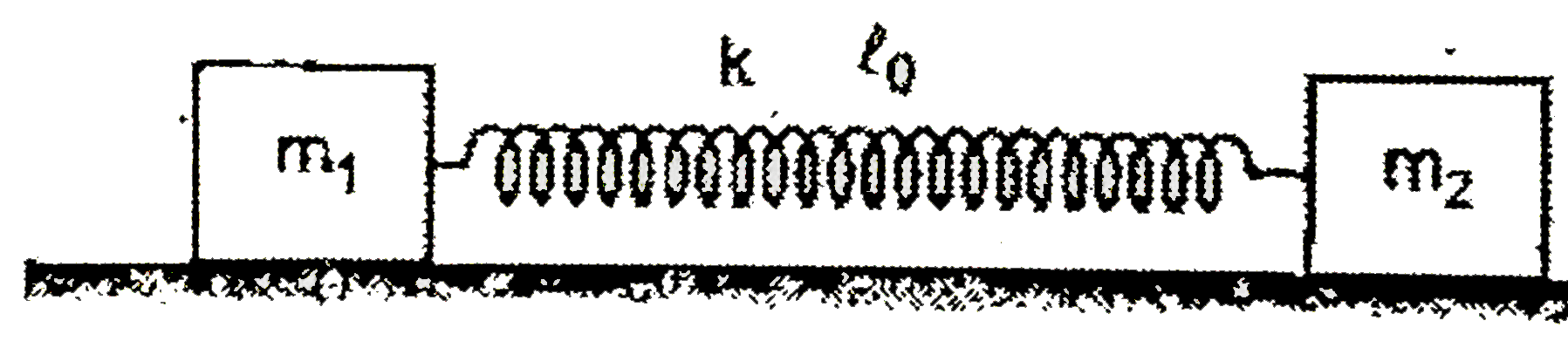
View Solution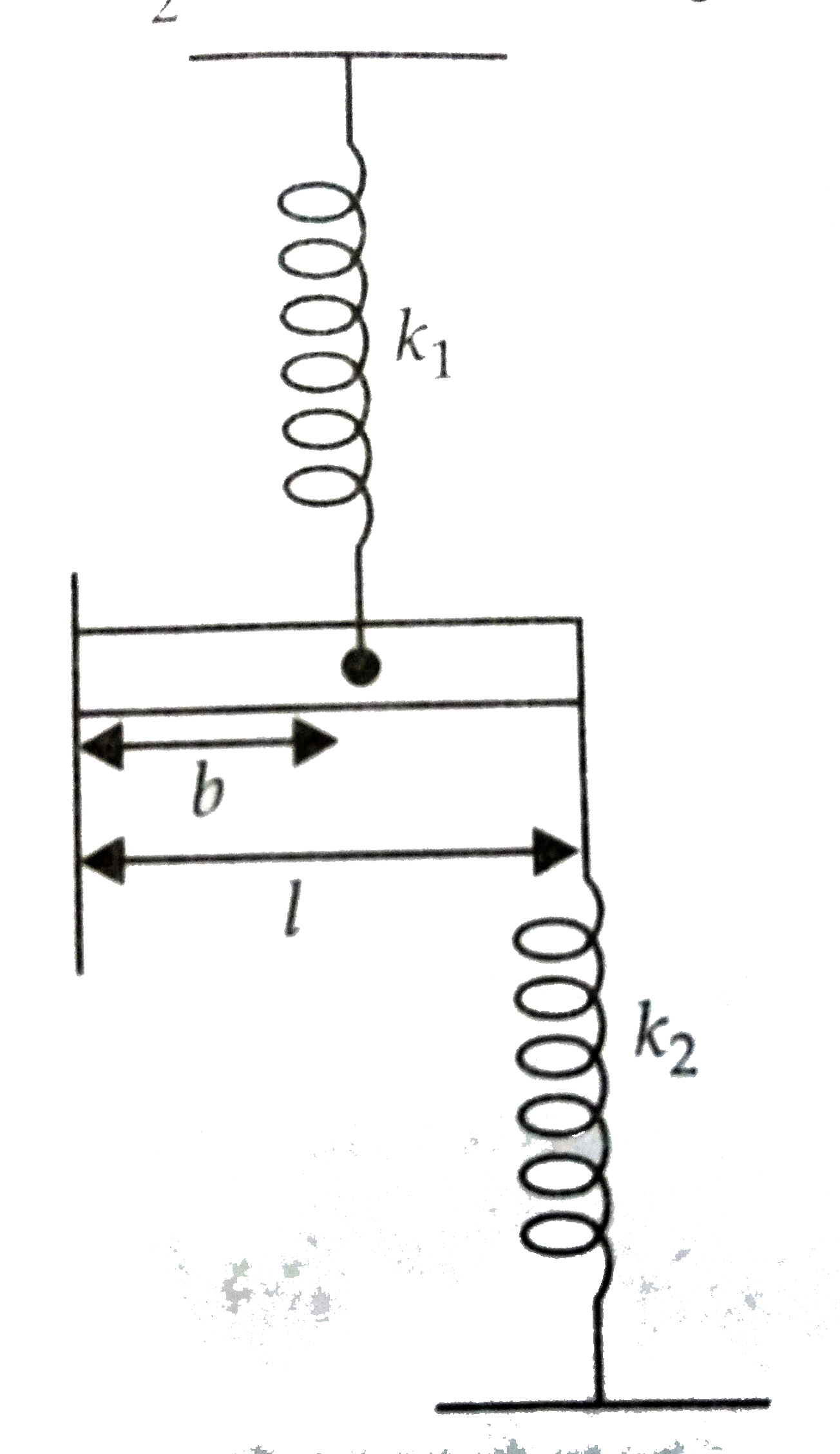
A rod of mass m and length l is connected by two spring of spring constants k1andk2, so that it is horizontal at equilibrium. What is the natural frequency of the system?
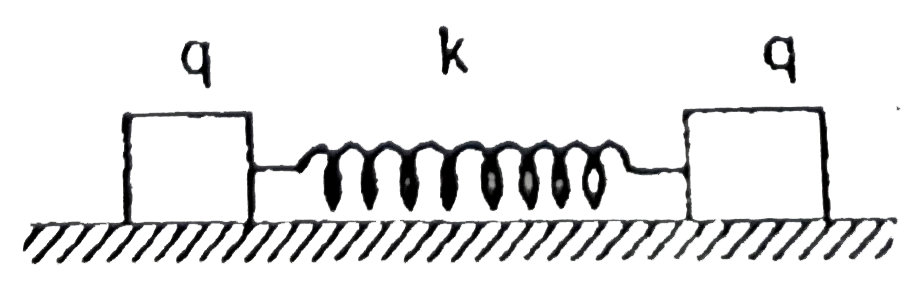
View SolutionTwo identical particles of charge q each are connected by a massless spring of force constant k. They are placed over a smooth horizontal surface. They are released when the separation between them is r and spring is unstretched. If maximum extension of the spring is r, the value of k is (neglect gravitational effect)
View SolutionA spring, placed horizontally on a rough surface is compressed by a block of mass m, placed on the same surface so as to store maximum energy in the spring. If the coefficient of friction between the block and the surface is μ, the potential energy stored in the spring is
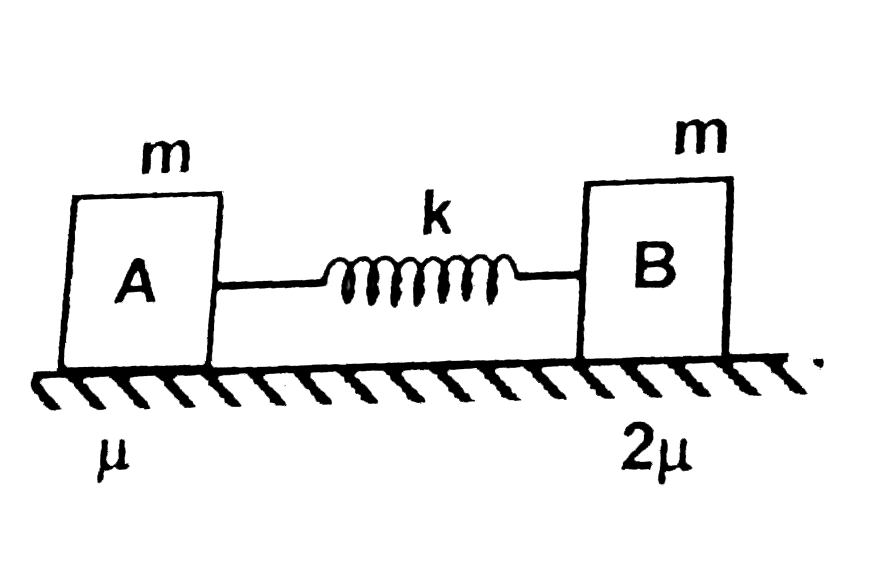
View SolutionTwo block of same mass'm' are joined with an dideal spring of spring constant k and sept on a rough surface as shown in figure. The spring is initially unstretched and coefficient of friction between the blocks and horizontal surface is μ and 2μ respectively. What should be the maximum speed of block 'A' such that the block 'B' does not move ?
View Solution

