A thin copper ring of radius a is charged with q units of electricity.An electron is placed at the centre of the copper ring .If the electron is displaced a little, it will have frequency
12π√eq4πε0ma3
12π√eq4πε0ema3
√eq4πε0ma
√q4πε0ema3
The correct Answer is:1
To find the frequency of oscillation of an electron placed at the center of a charged copper ring when it is slightly displaced, we can follow these steps:
1. Understanding the System:
- We have a thin copper ring of radius a charged with q units of electricity.
- An electron is placed at the center of the ring.
2. Electric Field at the Center:
- The electric field E at the center of the ring due to the uniformly charged ring is zero. This is because the contributions to the electric field from all parts of the ring cancel each other out.
3. Displacing the Electron:
- When the electron is displaced a small distance x from the center, it experiences a force due to the electric field generated by the ring.
4. Electric Field at a Distance x:
- The electric field E at a distance x from the center along the axis of the ring can be given by:
E=kqx(a2+x2)3/2
- Here, k is Coulomb's constant.
5. Force on the Electron:
- The force F on the electron when displaced by x is:
F=−eE=−e⋅kqx(a2+x2)3/2
- Where e is the charge of the electron.
6. Simplifying for Small Displacements:
- For small displacements where x is much smaller than a (i.e., x≪a), we can approximate:
E≈kqxa3
- Thus, the force becomes:
F≈−kqea3x
7. Relating Force to Acceleration:
- According to Newton's second law, F=ma, where m is the mass of the electron. Therefore:
ma=−kqea3x
- This can be rewritten as:
a=−kqema3x
8. Identifying Simple Harmonic Motion:
- The equation a=−ω2x indicates that the motion is simple harmonic with:
ω2=kqema3
9. Finding the Frequency:
- The frequency f of the oscillation is given by:
f=ω2π=12π√kqema3
Final Answer:
The frequency of oscillation of the electron when displaced slightly from the center of the charged copper ring is:
f=12π√kqema3
- We have a thin copper ring of radius a charged with q units of electricity.
- An electron is placed at the center of the ring.
- The electric field E at the center of the ring due to the uniformly charged ring is zero. This is because the contributions to the electric field from all parts of the ring cancel each other out.
- When the electron is displaced a small distance x from the center, it experiences a force due to the electric field generated by the ring.
- The electric field E at a distance x from the center along the axis of the ring can be given by:
E=kqx(a2+x2)3/2
- Here, k is Coulomb's constant.
- The force F on the electron when displaced by x is:
F=−eE=−e⋅kqx(a2+x2)3/2
- Where e is the charge of the electron.
- For small displacements where x is much smaller than a (i.e., x≪a), we can approximate:
E≈kqxa3
- Thus, the force becomes:
F≈−kqea3x
- According to Newton's second law, F=ma, where m is the mass of the electron. Therefore:
ma=−kqea3x
- This can be rewritten as:
a=−kqema3x
- The equation a=−ω2x indicates that the motion is simple harmonic with:
ω2=kqema3
- The frequency f of the oscillation is given by:
f=ω2π=12π√kqema3
The frequency of oscillation of the electron when displaced slightly from the center of the charged copper ring is:
f=12π√kqema3
Topper's Solved these Questions
- ELECTROSTATICS AND GAUSS LAWBOOK - NARAYNACHAPTER - ELECTROSTATICS AND GAUSS LAWEXERCISE - Level 1
8 Videos
- ELECTROSTATICS AND GAUSS LAWBOOK - NARAYNACHAPTER - ELECTROSTATICS AND GAUSS LAWEXERCISE - Level 2
10 Videos
- ELECTROSTATICS AND GAUSS LAWBOOK - NARAYNACHAPTER - ELECTROSTATICS AND GAUSS LAWEXERCISE - Level II(C.W)
27 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - NARAYNACHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - ADDITIONAL PROBLEMS
14 Videos
- EXPERIMENTAL PHYSICSBOOK - NARAYNACHAPTER - EXPERIMENTAL PHYSICSEXERCISE - Comprehension type
6 Videos
Similar Questions
A thin copper ring of radius a is charged with q units of electricity. Calculate the electric field at a point at a distance x from the centre and on the axis of the ring. Use the result to find the electirc field due to a charged disc of surface density of charge ε.
View SolutionA an electron is placed at the centre of the copper ring of problem 37. Show that if the electron is displaced a little, it will perform simple harmonic motion with a frequency f=12Π√eq4πε0ma3
View Solution
Knowledge Check
A thin conducting ring of radius R is given a charge +Q. The electric field at the centre O of the ring due to the charge on the part ABCD of the ring is
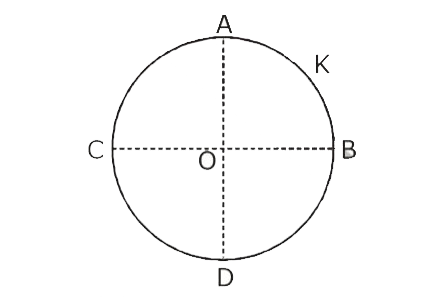 A3E along KOBE along OKCE along KOD3 E along OK
A3E along KOBE along OKCE along KOD3 E along OKA half ring of radius R has a charge of λ per unit length. The electric force on 1C charged placed at the center is
AzeroBkλRC2kλRD(kπλ)RA thin conducting ring of radius R is given a charge +Q, Fig. The electric field at the center O of the ring due to the charge on the part AKB of the ring is E. The electric field at the center due to the charge on part ACDB of the ring is
 A3E along KOBE along OKCE along KOD3E along OK
A3E along KOBE along OKCE along KOD3E along OK
A thin circular wire of radius r has a charge Q. If a point charge q is placed at the centre of the ring, then find the increase in tension in the wire.
View SolutionA quarter ring of radius R is having uniform charge density λ. Find the electric field and potential at the centre of the ring.
View SolutionA ring of radius R is with a uniformly distributed charge Q on it .A charge q is now placed in the centre of the ring .Find the increment in tension in the ring.
View SolutionA positive charge Q is uniformly distributed along a circular ring of radius. A small test charge q is placed at the centre of the ring. Then A. If q>0 and is displaced away from the centre in the plane of the ring., it will be pushed bactowards the centre.
B. If q<0 and is displced away from the centre in the plane of the ring, it will never return no the centre and will continue moving til it hits the ring.
C. If q<0, it will performe SHM for small displacement along the axis.
D. Q at the centre of the ring is in an unstable equilibrium within the plane of the ring for q>0
View SolutionA thin conducting ring orf radius R is given a chareg +Q, Fig. The electric field at the centre O of the ring due to the charge on the part AKB of the ring is E. The electric field at the centre due to the charge on part ACDB of the ring is

View Solution
